2.有毒水瓶问题2
2.1 题目
有 1000 瓶水,其中一瓶是有毒的,喝了会立即死亡。现在用小白鼠来测试哪一瓶水是有毒的。最少需要用多少只小白鼠才能测出哪一瓶是有毒的水?
2.2 深入解析
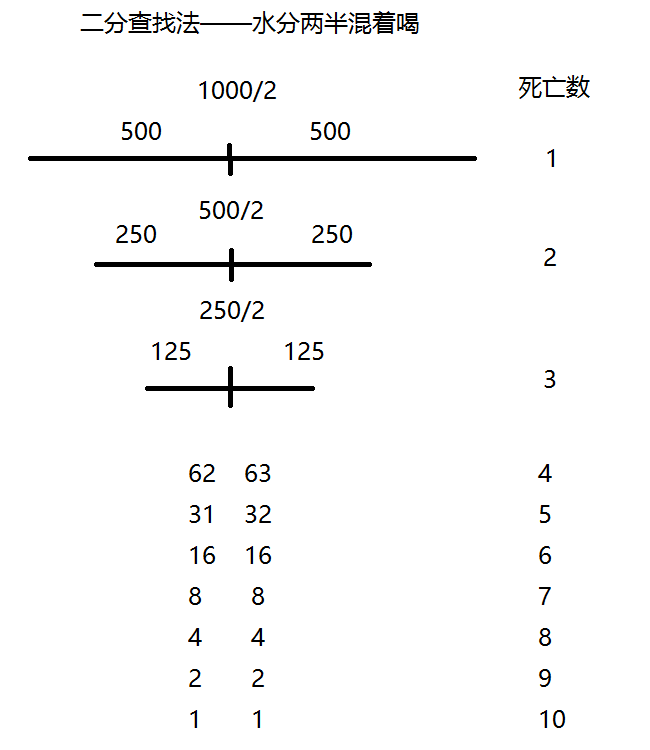
为了解决这个问题,可以采用二分查找法。具体步骤如下:
- 将 1000 瓶水分成两份,分别让小白鼠喝其中一份,剩下的一半不喝。
- 如果有毒的水在被喝的那一半里,那么至少会有一只小白鼠死亡。此时可以确定有毒的水在这一半里,剩下的问题就转化为在这一半水中找出有毒的瓶子。
- 继续将有毒的那半份水进行二分,重复上述步骤,直到找到有毒的瓶子。
通过二分查找法,最少只需要用 10 只小白鼠就能找到有毒的水瓶。因为二分查找的次数就是以 2 为底 1000 的对数,即 log2(1000) ≈ 9.97,向上取整为 10。
这种方法能够在最少的测试次数内找到有毒的水瓶,提高了测试效率。
2.3 答题示例
“最少需要10只小白鼠。解决思路基于二分查找法:
- 逐步缩小范围:将1000瓶水分成两份,让1只小白鼠喝下其中一份。若老鼠死亡,说明有毒水在这一半;若存活,则在另一份。
- 重复二分:对确定的有毒水所在的一半,再次分成两份,用新的小白鼠测试其中一份。每次测试都通过一只老鼠的生死状态,将范围缩小一半。
- 计算次数:因为每一步二分能将范围缩小至1/2,经过n次后可覆盖2ⁿ瓶水。由于2¹⁰=1024≥1000,所以经过10次二分即可精确锁定有毒水瓶。
这种方法通过每只老鼠负责一次二分测试,逐步缩小范围,最终用10只老鼠即可在10次测试后确定有毒的水。”
2.4 关键词联想
- 二分查找(Binary Search)
- 范围逐步缩小(Halving the Range)
- 对数计算(log₂(1000))
- 2ⁿ覆盖范围(2¹⁰=1024)
- 每次测试1只老鼠
- 生死状态作为判断依据
- 最坏情况测试次数
- 与“一次测试”场景的区别(分步测试)
转载请注明来源,欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。可以在下面评论区评论,也可以邮件至 785293209@qq.com

