104.二叉树的最大深度
104.1 题目
给定一个二叉树 root,返回其最大深度。
二叉树的最大深度是指从根节点到最远叶子节点的最长路径上的节点数。
示例 1: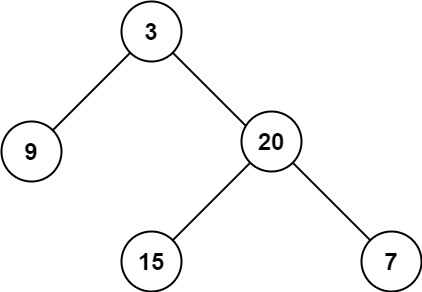
输入:root = [3,9,20,null,null,15,7]
输出:3
示例 2:
输入:root = [1,null,2]
输出:2
提示:
- 树中节点的数量在
[0, 10^4]区间内。 -100 <= Node.val <= 100
104.2 题解
递归
// 方法一:递归
// 先判空,递归计算左右子树的最大深度,返回较大者加1
static int MaxDepth1(TreeNode root)
{
// 如果当前节点为空(即递归到叶子节点的下一层),返回深度为0
if (root == null) return 0;
// 使用 Math.Max 函数计算左右子树的最大深度,递归调用 MaxDepth1 函数
// 1 + MaxDepth1(root.left) 表示左子树的深度加上当前节点的深度
// 1 + MaxDepth1(root.right) 表示右子树的深度加上当前节点的深度
// Math.Max 用于取两者中的较大值
return Math.Max(MaxDepth1(root.left), MaxDepth1(root.right)) + 1;
}
迭代(层序遍历)
// 方法二:迭代(层序遍历)
// 使用队列进行层序遍历,把每层的节点丢到队列中,下次循环出队把左右子节点丢进去,记录每一层的节点数和深度
static int MaxDepth2(TreeNode root)
{
// 如果当前节点为空(即递归到叶子节点的下一层),返回深度为0
if (root == null)
{
return 0;
}
// 创建一个队列,用于层序遍历二叉树
Queue<TreeNode> queue = new Queue<TreeNode>();
// 将根节点入队
queue.Enqueue(root);
// 初始化深度为0
int depth = 0;
// 使用 while 循环进行层序遍历
while (queue.Count > 0)
{
// 记录当前层的节点数
int levelSize = queue.Count;
// 遍历当前层的所有节点
for (int i = 0; i < levelSize; i++)
{
// 出队一个节点
TreeNode node = queue.Dequeue();
// 如果左子节点不为空,将左子节点入队
if (node.left != null)
{
queue.Enqueue(node.left);
}
// 如果右子节点不为空,将右子节点入队
if (node.right != null)
{
queue.Enqueue(node.right);
}
}
// 每完成一层的遍历,深度加1
depth++;
}
// 返回二叉树的深度
return depth;
}
104.3 代码
using System;
public class TreeNode
{
public int val;
public TreeNode left;
public TreeNode right;
public TreeNode(int x)
{
val = x;
}
}
class Program
{
static void Main()
{
#region 题目
// 给定一个二叉树 root ,返回其最大深度。
// 二叉树的最大深度是指从根节点到最远叶子节点的最长路径上的节点数。
// 示例 1:
// 输入:root = [3,9,20,null,null,15,7]
// 输出:3
// 示例 2:
// 输入:root = [1,null,2]
// 输出:2
// 提示:
// 树中节点的数量在 [0, 104] 区间内。
// -100 <= Node.val <= 100
#endregion
#region 测试
// 示例 1
TreeNode root1 = new TreeNode(3)
{
left = new TreeNode(9),
right = new TreeNode(20)
{
left = new TreeNode(15),
right = new TreeNode(7)
}
};
int result1 = MaxDepth1(root1);
Console.WriteLine($"示例1 方法1 输出:{result1}");
int result1_2 = MaxDepth2(root1);
Console.WriteLine($"示例1 方法2 输出:{result1_2}");
// 示例 2
TreeNode root2 = new TreeNode(1)
{
right = new TreeNode(2)
};
int result2 = MaxDepth1(root2);
Console.WriteLine($"示例2 方法1 输出:{result2}");
int result2_2 = MaxDepth2(root2);
Console.WriteLine($"示例2 方法2 输出:{result2_2}");
#endregion
}
#region 答案
// 方法一:递归
// 先判空,递归计算左右子树的最大深度,返回较大者加1
static int MaxDepth1(TreeNode root)
{
// 如果当前节点为空(即递归到叶子节点的下一层),返回深度为0
if (root == null) return 0;
// 使用 Math.Max 函数计算左右子树的最大深度,递归调用 MaxDepth1 函数
// 1 + MaxDepth1(root.left) 表示左子树的深度加上当前节点的深度
// 1 + MaxDepth1(root.right) 表示右子树的深度加上当前节点的深度
// Math.Max 用于取两者中的较大值
return Math.Max(MaxDepth1(root.left), MaxDepth1(root.right)) + 1;
}
// 方法二:迭代(层序遍历)
// 使用队列进行层序遍历,把每层的节点丢到队列中,下次循环出队把左右子节点丢进去,记录每一层的节点数和深度
static int MaxDepth2(TreeNode root)
{
// 如果当前节点为空(即递归到叶子节点的下一层),返回深度为0
if (root == null)
{
return 0;
}
// 创建一个队列,用于层序遍历二叉树
Queue<TreeNode> queue = new Queue<TreeNode>();
// 将根节点入队
queue.Enqueue(root);
// 初始化深度为0
int depth = 0;
// 使用 while 循环进行层序遍历
while (queue.Count > 0)
{
// 记录当前层的节点数
int levelSize = queue.Count;
// 遍历当前层的所有节点
for (int i = 0; i < levelSize; i++)
{
// 出队一个节点
TreeNode node = queue.Dequeue();
// 如果左子节点不为空,将左子节点入队
if (node.left != null)
{
queue.Enqueue(node.left);
}
// 如果右子节点不为空,将右子节点入队
if (node.right != null)
{
queue.Enqueue(node.right);
}
}
// 每完成一层的遍历,深度加1
depth++;
}
// 返回二叉树的深度
return depth;
}
#endregion
}
104.4 运行结果
示例1 方法1 输出:3
示例1 方法2 输出:3
示例2 方法1 输出:2
示例2 方法2 输出:2
转载请注明来源,欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。可以在下面评论区评论,也可以邮件至 785293209@qq.com

