11.盛最多水的容器
11.1 题目
给定一个长度为 n 的整数数组 height。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i])。找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。返回容器可以储存的最大水量。
说明: 你不能倾斜容器。
示例:
示例 1:
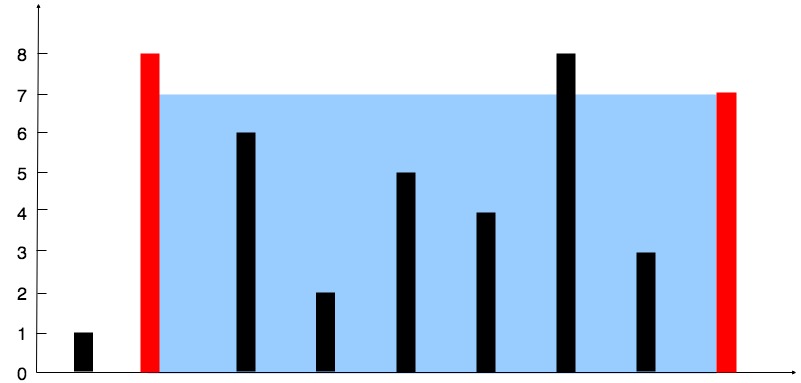
- 输入:
[1,8,6,2,5,4,8,3,7] - 输出:
49 - 解释:图中垂直线代表输入数组
[1,8,6,2,5,4,8,3,7]。在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为49。
- 输入:
示例 2:
- 输入:
height = [1,1] - 输出:
1
- 输入:
提示:
n == height.length2 <= n <= 10^50 <= height[i] <= 10^4
11.2 题解
双指针法
// 方法一:双指针法
// 双指针指向头和尾,更新记录最大储水量,每次移动高度较小的指针直到指针重叠
static int MaxArea1(int[] height)
{
// 初始化最大面积为0
int maxArea = 0;
// 初始化左右指针分别指向数组的两端
int left = 0, right = height.Length - 1;
// 使用双指针向中间移动,直到两指针相遇
while (left < right)
{
// 计算当前两指针所指位置形成的容器的高度
int h = Math.Min(height[left], height[right]);
// 计算当前容器的面积,并更新最大面积
maxArea = Math.Max(maxArea, h * (right - left));
// 移动高度较小的指针,以寻找可能更大的面积
if (height[left] < height[right])
left++;
else
right--;
}
// 返回最终的最大面积
return maxArea;
}
暴力法
// 方法二:暴力法
// 使用两层循环遍历所有可能的容器组合
static int MaxArea2(int[] height)
{
// 初始化最大面积为0
int maxArea = 0;
// 使用两层循环遍历所有可能的容器组合
for (int i = 0; i < height.Length - 1; i++)
{
for (int j = i + 1; j < height.Length; j++)
{
// 计算当前两指针所指位置形成的容器的高度
int h = Math.Min(height[i], height[j]);
// 计算当前容器的面积,并更新最大面积
maxArea = Math.Max(maxArea, h * (j - i));
}
}
// 返回最终的最大面积
return maxArea;
}
11.3 代码
using System;
class Program
{
static void Main()
{
#region 题目
// 给定一个长度为 n 的整数数组 height 。
// 有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。
// 找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
// 返回容器可以储存的最大水量。
// 说明:你不能倾斜容器。
// 示例 1:
// 输入:[1,8,6,2,5,4,8,3,7]
// 输出:49
// 解释:图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。
// 在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。
// 示例 2:
// 输入:height = [1,1]
// 输出:1
// 提示:
// n == height.length
// 2 <= n <= 105
// 0 <= height[i] <= 104
#endregion
#region 测试
// 示例 1
int[] height1 = { 1, 8, 6, 2, 5, 4, 8, 3, 7 };
int result1 = MaxArea1(height1);
Console.WriteLine($"示例1 方法1 输出:{result1}");
int result1_2 = MaxArea2(height1);
Console.WriteLine($"示例1 方法2 输出:{result1_2}");
// 示例 2
int[] height2 = { 1, 1 };
int result2 = MaxArea1(height2);
Console.WriteLine($"示例2 方法1 输出:{result2}");
int result2_2 = MaxArea2(height2);
Console.WriteLine($"示例2 方法2 输出:{result2_2}");
#endregion
}
#region 答案
// 方法一:双指针法
// 双指针指向头和尾,更新记录最大储水量,每次移动高度较小的指针直到指针重叠
static int MaxArea1(int[] height)
{
// 初始化最大面积为0
int maxArea = 0;
// 初始化左右指针分别指向数组的两端
int left = 0, right = height.Length - 1;
// 使用双指针向中间移动,直到两指针相遇
while (left < right)
{
// 计算当前两指针所指位置形成的容器的高度
int h = Math.Min(height[left], height[right]);
// 计算当前容器的面积,并更新最大面积
maxArea = Math.Max(maxArea, h * (right - left));
// 移动高度较小的指针,以寻找可能更大的面积
if (height[left] < height[right])
left++;
else
right--;
}
// 返回最终的最大面积
return maxArea;
}
// 方法二:暴力法
// 使用两层循环遍历所有可能的容器组合
static int MaxArea2(int[] height)
{
// 初始化最大面积为0
int maxArea = 0;
// 使用两层循环遍历所有可能的容器组合
for (int i = 0; i < height.Length - 1; i++)
{
for (int j = i + 1; j < height.Length; j++)
{
// 计算当前两指针所指位置形成的容器的高度
int h = Math.Min(height[i], height[j]);
// 计算当前容器的面积,并更新最大面积
maxArea = Math.Max(maxArea, h * (j - i));
}
}
// 返回最终的最大面积
return maxArea;
}
#endregion
}
11.4 运行结果
示例1 方法1 输出:49
示例1 方法2 输出:49
示例2 方法1 输出:1
示例2 方法2 输出:1
转载请注明来源,欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。可以在下面评论区评论,也可以邮件至 785293209@qq.com

