118.杨辉三角

LeetCode LeetCode 数组 动态规划
发布时间 :
字数:1.6k 阅读 : 评论:
  1. 118.杨辉三角
    1. 118.1 题目
    2. 118.2 题解
      1. 递归法
      2. 迭代法
    3. 118.3 代码
    4. 118.4 运行结果

118.杨辉三角

118.1 题目

给定一个非负整数 numRows，生成「杨辉三角」的前 numRows 行。

在「杨辉三角」中，每个数是它左上方和右上方的数的和。

示例 1: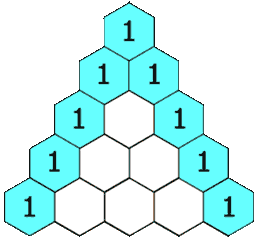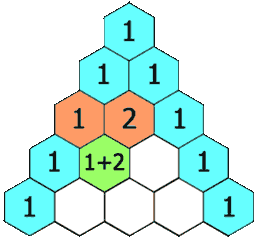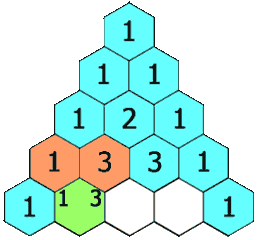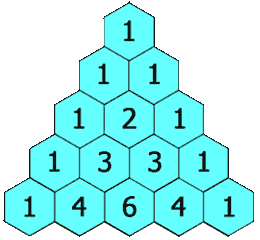

输入: numRows = 5
输出: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]

示例 2:

输入: numRows = 1
输出: [[1]]

提示:

  • 1 <= numRows <= 30

118.2 题解

递归法

// 方法一：递归法
// 递归获取杨辉三角的数字,递归是判断当前位置是否是三角的边界位置，如果是，返回1，不是的话返回递归获取左上方和右上方的数字之和
public static IList<IList<int>> Generate1(int numRows)
{
    // 初始化最终结果列表
    IList<IList<int>> result = new List<IList<int>>();

    // 使用字典缓存计算结果，避免重复计算
    Dictionary<(int, int), int> memo = new Dictionary<(int, int), int>();

    // 从第1层开始逐层构建杨辉三角
    for (int nowLayer = 1; nowLayer <= numRows; nowLayer++)
    {
        // 初始化当前层的列表
        List<int> nowLayerList = new List<int>();

        // 填充当前层的每一个元素
        for (int nowIndex = 0; nowIndex < nowLayer; nowIndex++)
        {
            // 获取当前层当前索引位置的值
            nowLayerList.Add(GetYangHuiVal(nowLayer, nowIndex, memo));
        }

        // 将当前层添加到最终结果中
        result.Add(nowLayerList);
    }

    // 返回构建好的杨辉三角
    return result;
}

// 递归获取杨辉三角某个位置的值，使用memo缓存中间结果
private static int GetYangHuiVal(int layer, int index, Dictionary<(int, int), int> memo)
{
    // 如果是第一列或最后一列，值为1
    if (index == 0 || index == layer - 1) return 1;

    // 如果缓存中已有该位置的值，则直接返回
    if (memo.ContainsKey((layer, index)))
    {
        return memo[(layer, index)];
    }

    // 递归获取上层左边和上层右边的值，并求和得到当前值
    int value = GetYangHuiVal(layer - 1, index - 1, memo) + GetYangHuiVal(layer - 1, index, memo);

    // 将计算结果存入缓存
    memo[(layer, index)] = value;

    // 返回当前值
    return value;
}

迭代法

// 方法二：迭代法
// 双循环遍历生成杨辉三角形
static IList<IList<int>> Generate2(int numRows)
{
    // 用于存储生成的杨辉三角
    IList<IList<int>> triangle = new List<IList<int>>();

    // 遍历每一行
    for (int i = 0; i < numRows; i++)
    {
        // 用于存储当前行的数字
        List<int> row = new List<int>();

        // 遍历当前行的每个位置
        for (int j = 0; j <= i; j++)
        {
            // 如果是三角的边界位置，直接添加1
            if (j == 0 || j == i)
            {
                row.Add(1);
            }
            else
            {
                // 添加左上方和右上方的数字之和
                row.Add(triangle[i - 1][j - 1] + triangle[i - 1][j]);
            }
        }

        // 将当前行添加到杨辉三角
        triangle.Add(row);
    }

    // 返回生成的杨辉三角
    return triangle;
}

118.3 代码

using System;
using System.Collections.Generic;

class Program
{
    static void Main()
    {
        #region 题目

        // 给定一个非负整数 numRows，生成「杨辉三角」的前 numRows 行。
        // 在「杨辉三角」中，每个数是它左上方和右上方的数的和。

        // 示例 1:
        // 输入: numRows = 5
        // 输出: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]

        // 示例 2:
        // 输入: numRows = 1
        // 输出: [[1]]

        // 提示:
        // 1 <= numRows <= 30

        #endregion

        #region 测试

        // 示例 1
        int numRows1 = 5;
        IList<IList<int>> result1 = Generate1(numRows1);
        Console.WriteLine($"示例1 方法1 输出：{PrintResult(result1)}");
        IList<IList<int>> result1_2 = Generate2(numRows1);
        Console.WriteLine($"示例1 方法2 输出：{PrintResult(result1_2)}");

        // 示例 2
        int numRows2 = 1;
        IList<IList<int>> result2 = Generate1(numRows2);
        Console.WriteLine($"示例2 方法1 输出：{PrintResult(result2)}");
        IList<IList<int>> result2_2 = Generate2(numRows2);
        Console.WriteLine($"示例2 方法2 输出：{PrintResult(result2_2)}");

        #endregion
    }

    #region 答案

    // 方法一：递归法
    // 递归获取杨辉三角的数字,递归是判断当前位置是否是三角的边界位置，如果是，返回1，不是的话返回递归获取左上方和右上方的数字之和
    public static IList<IList<int>> Generate1(int numRows)
    {
        // 初始化最终结果列表
        IList<IList<int>> result = new List<IList<int>>();

        // 使用字典缓存计算结果，避免重复计算
        Dictionary<(int, int), int> memo = new Dictionary<(int, int), int>();

        // 从第1层开始逐层构建杨辉三角
        for (int nowLayer = 1; nowLayer <= numRows; nowLayer++)
        {
            // 初始化当前层的列表
            List<int> nowLayerList = new List<int>();

            // 填充当前层的每一个元素
            for (int nowIndex = 0; nowIndex < nowLayer; nowIndex++)
            {
                // 获取当前层当前索引位置的值
                nowLayerList.Add(GetYangHuiVal(nowLayer, nowIndex, memo));
            }

            // 将当前层添加到最终结果中
            result.Add(nowLayerList);
        }

        // 返回构建好的杨辉三角
        return result;
    }

    // 递归获取杨辉三角某个位置的值，使用memo缓存中间结果
    private static int GetYangHuiVal(int layer, int index, Dictionary<(int, int), int> memo)
    {
        // 如果是第一列或最后一列，值为1
        if (index == 0 || index == layer - 1) return 1;

        // 如果缓存中已有该位置的值，则直接返回
        if (memo.ContainsKey((layer, index)))
        {
            return memo[(layer, index)];
        }

        // 递归获取上层左边和上层右边的值，并求和得到当前值
        int value = GetYangHuiVal(layer - 1, index - 1, memo) + GetYangHuiVal(layer - 1, index, memo);

        // 将计算结果存入缓存
        memo[(layer, index)] = value;

        // 返回当前值
        return value;
    }

    // 方法二：迭代法
    // 双循环遍历生成杨辉三角形
    static IList<IList<int>> Generate2(int numRows)
    {
        // 用于存储生成的杨辉三角
        IList<IList<int>> triangle = new List<IList<int>>();

        // 遍历每一行
        for (int i = 0; i < numRows; i++)
        {
            // 用于存储当前行的数字
            List<int> row = new List<int>();

            // 遍历当前行的每个位置
            for (int j = 0; j <= i; j++)
            {
                // 如果是三角的边界位置，直接添加1
                if (j == 0 || j == i)
                {
                    row.Add(1);
                }
                else
                {
                    // 添加左上方和右上方的数字之和
                    row.Add(triangle[i - 1][j - 1] + triangle[i - 1][j]);
                }
            }

            // 将当前行添加到杨辉三角
            triangle.Add(row);
        }

        // 返回生成的杨辉三角
        return triangle;
    }

    // 打印结果
    static string PrintResult(IList<IList<int>> result)
    {
        string output = "[";
        foreach (List<int> row in result)
        {
            output += "[";
            foreach (int num in row)
            {
                output += num + ",";
            }

            output = output.TrimEnd(',') + "],";
        }

        output = output.TrimEnd(',') + "]";
        return output;
    }

    #endregion
}

118.4 运行结果

示例1 方法1 输出：[[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]
示例1 方法2 输出：[[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]
示例2 方法1 输出：[[1]]
示例2 方法2 输出：[[1]]
转载请注明来源，欢迎对文章中的引用来源进行考证，欢迎指出任何有错误或不够清晰的表达。可以在下面评论区评论，也可以邮件至 785293209@qq.com

赏

©2016-2024 Tao

Built with Hexo and 3-hexo theme

×

喜欢就点赞,疼爱就打赏