287.寻找重复数

LeetCode LeetCode 数组 双指针
发布时间 :
字数:2.1k 阅读 : 评论:
  1. 287.寻找重复数
    1. 287.1 题目
    2. 287.2 题解
      1. 快慢指针
      2. 二分查找
    3. 287.3 代码
    4. 287.4 运行结果

287.寻找重复数

287.1 题目

给定一个包含 n + 1 个整数的数组 nums，其数字都在 [1, n] 范围内（包括 1 和 n），可知至少存在一个重复的整数。

假设 nums 只有一个重复的整数，返回这个重复的数。

你设计的解决方案必须不修改数组 nums 且只用常量级 O(1) 的额外空间。

示例 1：

输入：nums = [1,3,4,2,2]
输出：2

示例 2：

输入：nums = [3,1,3,4,2]
输出：3

示例 3：

输入：nums = [3,3,3,3,3]
输出：3

提示：

  • 1 <= n <= 10^5
  • nums.length == n + 1
  • 1 <= nums[i] <= n
  • nums 中只有一个整数出现两次或多次，其余整数均只出现一次

进阶：

如何证明 nums 中至少存在一个重复的数字?
你可以设计一个线性级时间复杂度 O(n) 的解决方案吗？

287.2 题解

快慢指针

  • 链表中的环
    假设有这样一个样例：[1,2,3,4,5,6,7,8,9,5]。如果我们按照上面的循环下去就会得到这样一个路径：1 2 3 4 5 [6 7 8 9] [6 7 8 9] [6 7 8 9] . . .这样就有了一个环，也就是 6 7 8 9。point 会一直在环中循环的前进。
    这时我们设置两个一快(fast)一慢(slow)两个指针，一个每次走两步，一个每次走一步，这样让他们一直走下去，直到他们在重复的序列中相遇，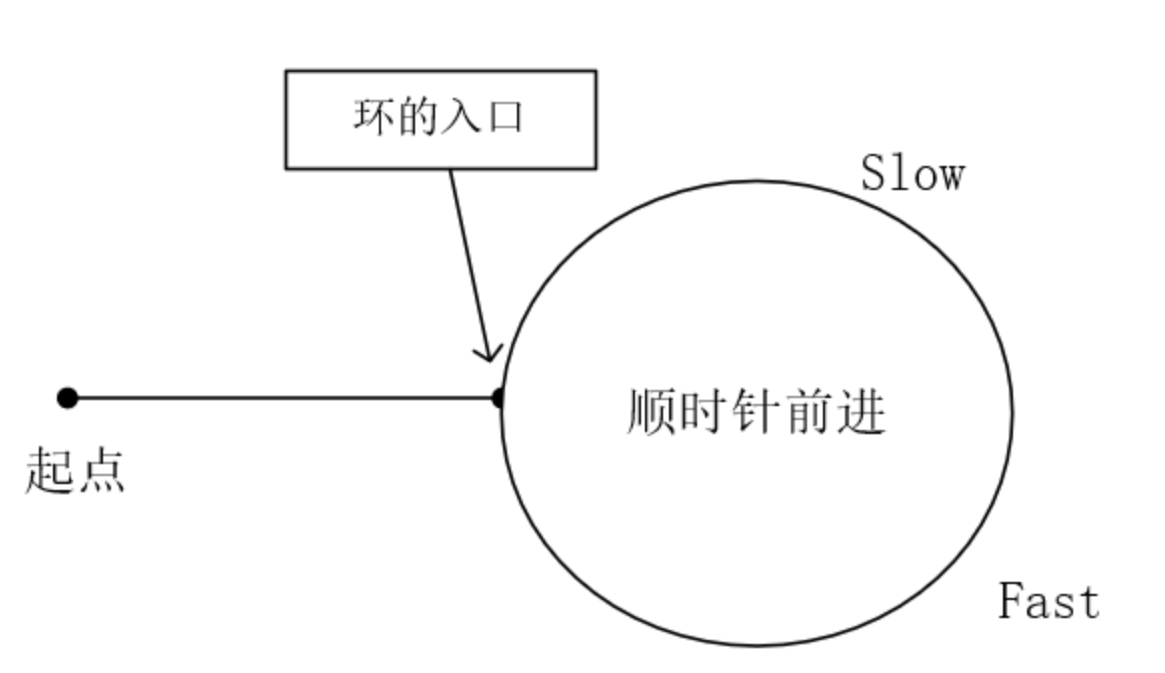

    如上图，slow 和 fast 会在环中相遇，先假设一些量：起点到环的入口长度为 m，环的周长为 c，在 fast 和 slow 相遇时 slow 走了 n 步。则 fast 走了 2n 步，fast 比 slow 多走了 n 步，而这 n 步全用在了在环里循环（n%c==0）。
    当 fast 和 last 相遇之后，我们设置第三个指针 finder，它从起点开始和 slow(在 fast 和 slow 相遇处)同步前进，当 finder 和 slow 相遇时，就是在环的入口处相遇，也就是重复的那个数字相遇

  • 为什么 finder 和 slow 相遇在入口
    fast 和 slow 相遇时，slow 在环中行进的距离是 n-m，其中 n%c == 0。这时我们再让 slow 前进 m 步——也就是在环中走了 n 步了。而 n%c==0 即 slow 在环里面走的距离是环的周长的整数倍，就回到了环的入口了，而入口就是重复的数字。
    我们不知道起点到入口的长度 m，所以弄个 finder 和 slow 一起走，他们必定会在入口处相遇。

// 方法一：快慢指针（Floyd 判圈算法）
static int FindDuplicate1(int[] nums)
{
    // 初始化快慢指针
    int fast = 0, slow = 0;

    // 第一阶段：找到快慢指针相遇点
    while (true)
    {
        // 快指针每次走两步
        fast = nums[nums[fast]]; // 快指针移动两步，nums[fast] 是下一个索引的值，再取一次 nums 数组得到下一个位置的值
        // 慢指针每次走一步
        slow = nums[slow]; // 慢指针移动一步

        // 判断快慢指针是否相遇
        if (fast == slow)
            break; // 如果相遇，退出循环
    }

    // 第二阶段：找到环的入口（即重复的数字）
    int finder = 0;
    while (true)
    {
        // finder 和 slow 每次都向前移动一步
        finder = nums[finder]; // finder 向前移动一步
        slow = nums[slow]; // slow 向前移动一步

        // 判断 finder 和 slow 是否相等，相等即找到了重复的数字（环的入口）
        if (slow == finder)
            break; // 如果相等，退出循环
    }

    return slow; // 返回重复的数字
}

二分查找

// 方法二：二分查找
// 使用二分查找的方法，通过统计输入数组中小于等于中间值的元素个数来确定重复的数字范围。
// 根据统计结果调整搜索范围，直到找到重复的数字。
static int FindDuplicate2(int[] nums)
{
    // 初始化左右边界 比如5个数 就设定范围是 1-4
    int left = 1;
    int right = nums.Length - 1;

    // 二分查找
    while (left < right)
    {
        // 中间值 比如1-4中间值就是2
        int mid = left + (right - left) / 2;

        // 统计数组中小于等于中间值的元素个数 比如小于等于2的元素有3个
        int count = 0;
        foreach (int num in nums)
        {
            if (num <= mid)
            {
                count++;
            }
        }

        // 根据统计结果调整左右边界 比如小于等于2的元素有3个 那么多出来的元素在数组左边
        if (count > mid)
        {
            right = mid;
        }
        else //否则在右边
        {
            left = mid + 1;
        }
    }

    // 返回重复的数
    return left;
}

287.3 代码

using System;

class Program
{
    static void Main()
    {
        #region 题目

        // 给定一个包含 n + 1 个整数的数组 nums ，其数字都在 [1, n] 范围内（包括 1 和 n），可知至少存在一个重复的整数。
        // 假设 nums 只有 一个重复的整数 ，返回 这个重复的数 。
        // 你设计的解决方案必须 不修改 数组 nums 且只用常量级 O(1) 的额外空间。

        // 示例 1：
        // 输入：nums = [1,3,4,2,2]
        // 输出：2

        // 示例 2：
        // 输入：nums = [3,1,3,4,2]
        // 输出：3

        // 示例 3 :
        // 输入：nums = [3,3,3,3,3]
        // 输出：3

        // 提示：
        // 1 <= n <= 105
        // nums.length == n + 1
        // 1 <= nums[i] <= n
        // nums 中 只有一个整数 出现 两次或多次 ，其余整数均只出现 一次

        // 进阶：
        // 如何证明 nums 中至少存在一个重复的数字?
        // 你可以设计一个线性级时间复杂度 O(n) 的解决方案吗？

        #endregion

        #region 测试

        // 示例 1
        int[] nums1 = { 1, 3, 4, 2, 2 };
        int result1 = FindDuplicate1(nums1);
        Console.WriteLine($"示例1 方法1 输出：{result1}");
        int result1_2 = FindDuplicate2(nums1);
        Console.WriteLine($"示例1 方法2 输出：{result1_2}");

        // 示例 2
        int[] nums2 = { 3, 1, 3, 4, 2 };
        int result2 = FindDuplicate1(nums2);
        Console.WriteLine($"示例2 方法1 输出：{result2}");
        int result2_2 = FindDuplicate2(nums2);
        Console.WriteLine($"示例2 方法2 输出：{result2_2}");

        // 示例 3
        int[] nums3 = { 3, 3, 3, 3, 3 };
        int result3 = FindDuplicate1(nums3);
        Console.WriteLine($"示例3 方法1 输出：{result3}");
        int result3_2 = FindDuplicate2(nums3);
        Console.WriteLine($"示例3 方法2 输出：{result3_2}");

        #endregion
    }

    #region 答案

    // 方法一：快慢指针（Floyd 判圈算法）
    static int FindDuplicate1(int[] nums)
    {
        // 初始化快慢指针
        int fast = 0, slow = 0;

        // 第一阶段：找到快慢指针相遇点
        while (true)
        {
            // 快指针每次走两步
            fast = nums[nums[fast]]; // 快指针移动两步，nums[fast] 是下一个索引的值，再取一次 nums 数组得到下一个位置的值
            // 慢指针每次走一步
            slow = nums[slow]; // 慢指针移动一步

            // 判断快慢指针是否相遇
            if (fast == slow)
                break; // 如果相遇，退出循环
        }

        // 第二阶段：找到环的入口（即重复的数字）
        int finder = 0;
        while (true)
        {
            // finder 和 slow 每次都向前移动一步
            finder = nums[finder]; // finder 向前移动一步
            slow = nums[slow]; // slow 向前移动一步

            // 判断 finder 和 slow 是否相等，相等即找到了重复的数字（环的入口）
            if (slow == finder)
                break; // 如果相等，退出循环
        }

        return slow; // 返回重复的数字
    }


    // 方法二：二分查找
    // 使用二分查找的方法，通过统计输入数组中小于等于中间值的元素个数来确定重复的数字范围。
    // 根据统计结果调整搜索范围，直到找到重复的数字。
    static int FindDuplicate2(int[] nums)
    {
        // 初始化左右边界 比如5个数 就设定范围是 1-4
        int left = 1;
        int right = nums.Length - 1;

        // 二分查找
        while (left < right)
        {
            // 中间值 比如1-4中间值就是2
            int mid = left + (right - left) / 2;

            // 统计数组中小于等于中间值的元素个数 比如小于等于2的元素有3个
            int count = 0;
            foreach (int num in nums)
            {
                if (num <= mid)
                {
                    count++;
                }
            }

            // 根据统计结果调整左右边界 比如小于等于2的元素有3个 那么多出来的元素在数组左边
            if (count > mid)
            {
                right = mid;
            }
            else //否则在右边
            {
                left = mid + 1;
            }
        }

        // 返回重复的数
        return left;
    }

    #endregion
}

287.4 运行结果

示例1 方法1 输出：2
示例1 方法2 输出：2
示例2 方法1 输出：3
示例2 方法2 输出：3
示例3 方法1 输出：3
示例3 方法2 输出：3
转载请注明来源，欢迎对文章中的引用来源进行考证，欢迎指出任何有错误或不够清晰的表达。可以在下面评论区评论，也可以邮件至 785293209@qq.com

赏

©2016-2024 Tao

Built with Hexo and 3-hexo theme

×

喜欢就点赞,疼爱就打赏