24.总结

892.三维形体的表面积

---

892.1 题目

给你一个 n * n 的网格 grid，上面放置着一些 1 x 1 x 1 的正方体。每个值 v = grid[i][j] 表示 v 个正方体叠放在对应单元格 (i, j) 上。

放置好正方体后，任何直接相邻的正方体都会互相粘在一起，形成一些不规则的三维形体。

请你返回最终这些形体的总表面积。

注意：每个形体的底面也需要计入表面积中。

示例 1：

输入：grid = [[1,2],[3,4]]
输出：34

示例 2：

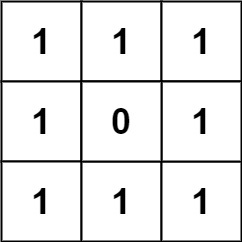
输入：grid = [[1,1,1],[1,0,1],[1,1,1]]
输出：32

示例 3：

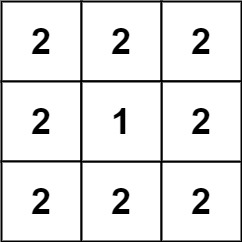
输入：grid = [[2,2,2],[2,1,2],[2,2,2]]
输出：46

提示：

• n == grid.length
• n == grid[i].length
• 1 <= n <= 50
• 0 <= grid[i][j] <= 50

---

892.2 题解

遍历计算表面积

// 方法一：遍历计算表面积
// 遍历每个格子，使用表面积计算公式计算后，减去上左重叠的面积
static int SurfaceArea1(int[][] grid)
{
    // 获取网格的长度（假设网格是 n * n 的正方形）
    int gridLength = grid.Length;

    // 初始化表面积为 0
    int surfaceArea = 0;

    // 遍历每个单元格
    for (int nowX = 0; nowX < gridLength; nowX++)
    {
        for (int nowY = 0; nowY < gridLength; nowY++)
        {
            // 获取当前单元格的高度值
            int heightValue = grid[nowX][nowY];

            // 计算当前单元格的表面积
            if (heightValue > 0)
            {
                // 表面积计算公式：4 * 高度值 + 2（每个单元格的底面积为1，所以加2）
                surfaceArea += 4 * heightValue + 2;

                // 减去相邻重叠的部分 只考虑上和左即可 下和右上后面的单元格考虑上和左计算的
                // 如果当前单元格不在第一行，则减去与上方单元格的重叠面积。重叠面积是两者高度差乘2，因为重叠一次减少2表面积。
                if (nowX > 0) surfaceArea -= Math.Min(heightValue, grid[nowX - 1][nowY]) * 2;

                // 如果当前单元格不在第一列，则减去与左方单元格的重叠面积。重叠面积是两者高度差乘2，因为重叠一次减少2表面积。
                if (nowY > 0) surfaceArea -= Math.Min(heightValue, grid[nowX][nowY - 1]) * 2;
            }
        }
    }

    // 返回最终计算得到的表面积
    return surfaceArea;
}

---

892.3 代码

using System;

class Program
{
    static void Main()
    {
        #region 题目

        // 给定一个 n * n 的网格 grid ，上面放置着一些 1 x 1 x 1 的正方体。
        // 每个值 v = grid[i][j] 表示 v 个正方体叠放在对应单元格 (i, j) 上。
        // 放置好正方体后，任何直接相邻的正方体都会互相粘在一起，形成一些不规则的三维形体。
        // 请你返回最终这些形体的总表面积。

        // 注意：每个形体的底面也需要计入表面积中。

        // 示例 1：
        // 输入：grid = [[1,2],[3,4]]
        // 输出：34

        // 示例 2：
        // 输入：grid = [[1,1,1],[1,0,1],[1,1,1]]
        // 输出：32

        // 示例 3：
        // 输入：grid = [[2,2,2],[2,1,2],[2,2,2]]
        // 输出：46

        #endregion

        #region 测试

        // 示例 1
        int[][] grid1 = { new int[] { 1, 2 }, new int[] { 3, 4 } };
        int result1_1 = SurfaceArea1(grid1);
        Console.WriteLine($"示例1 方法1 输出：{result1_1}");

        // 示例 2
        int[][] grid2 = { new int[] { 1, 1, 1 }, new int[] { 1, 0, 1 }, new int[] { 1, 1, 1 } };
        int result2_1 = SurfaceArea1(grid2);
        Console.WriteLine($"示例2 方法1 输出：{result2_1}");

        // 示例 3
        int[][] grid3 = { new int[] { 2, 2, 2 }, new int[] { 2, 1, 2 }, new int[] { 2, 2, 2 } };
        int result3_1 = SurfaceArea1(grid3);
        Console.WriteLine($"示例3 方法1 输出：{result3_1}");

        #endregion
    }

    #region 答案

    // 方法一：遍历计算表面积
    // 遍历每个格子，使用表面积计算公式计算后，减去上左重叠的面积
    static int SurfaceArea1(int[][] grid)
    {
        // 获取网格的长度（假设网格是 n * n 的正方形）
        int gridLength = grid.Length;

        // 初始化表面积为 0
        int surfaceArea = 0;

        // 遍历每个单元格
        for (int nowX = 0; nowX < gridLength; nowX++)
        {
            for (int nowY = 0; nowY < gridLength; nowY++)
            {
                // 获取当前单元格的高度值
                int heightValue = grid[nowX][nowY];

                // 计算当前单元格的表面积
                if (heightValue > 0)
                {
                    // 表面积计算公式：4 * 高度值 + 2（每个单元格的底面积为1，所以加2）
                    surfaceArea += 4 * heightValue + 2;

                    // 减去相邻重叠的部分 只考虑上和左即可 下和右上后面的单元格考虑上和左计算的
                    // 如果当前单元格不在第一行，则减去与上方单元格的重叠面积。重叠面积是两者高度差乘2，因为重叠一次减少2表面积。
                    if (nowX > 0) surfaceArea -= Math.Min(heightValue, grid[nowX - 1][nowY]) * 2;

                    // 如果当前单元格不在第一列，则减去与左方单元格的重叠面积。重叠面积是两者高度差乘2，因为重叠一次减少2表面积。
                    if (nowY > 0) surfaceArea -= Math.Min(heightValue, grid[nowX][nowY - 1]) * 2;
                }
            }
        }

        // 返回最终计算得到的表面积
        return surfaceArea;
    }

    #endregion
}

---

892.4 运行结果

示例1 方法1 输出：34
示例2 方法1 输出：32
示例3 方法1 输出：46

---

---

转载请注明来源，欢迎对文章中的引用来源进行考证，欢迎指出任何有错误或不够清晰的表达。可以在下面评论区评论，也可以邮件至 785293209@qq.com