11.Quaternion四元数是什么

游戏引擎 > Unity > Unity基础 > Unity基础基础知识游戏引擎 Unity Unity基础 Unity基础基础知识 3D数学

发布时间 : 2024-02-28 22:38

字数:1.5k 阅读 :

评论:

11.3D数学-Quaternion四元数-四元数是什么
1. 11.1 知识点
2. 11.2 知识点代码

11.3D数学-Quaternion四元数-四元数是什么

11.1 知识点

知识回顾

主要学习内容

四元数构成

轴角对

Unity中的四元数 Quaternion

四元数由一个向量(x,y,z)和要旋转的角度β通过数学运算构成。
四元数Q = [cos(β/2), sin(β/2)x, sin(β/2)y, sin(β/2)z]

Quaternion的构造函数初始化四元数

//用四元数的计算原理 绕着(x,y,z)向量旋转β度 要传入弧度制 角度转弧度
//Quaternion q = new Quaternion(Mathf.Sin(β/2 * Mathf.Deg2Rad)*x, Mathf.Sin(β/2 * Mathf.Deg2Rad)*y, Mathf.Sin(β/2 * Mathf.Deg2Rad)*z, Mathf.Cos(β/2 * Mathf.Deg2Rad));
//绕着(1,0,0)向量旋转60度 要传入弧度制 角度转弧度
Quaternion q1 = new Quaternion(Mathf.Sin(30 * Mathf.Deg2Rad), 0, 0, Mathf.Cos(30 * Mathf.Deg2Rad));

AngleAxis静态方法绕着某一个向量旋转多少度

AngleAxis静态方法用于创建一个围绕轴向量旋转指定角度的四元数。

//创建一个围绕 axis 旋转 offsetAngle 度的旋转。
//提供的轴角对 初始化 四元数的方法 分别传入度数和向量轴
Quaternion q2 = Quaternion.AngleAxis(60, Vector3.right);

创建一个立方体演示

GameObject obj = GameObject.CreatePrimitive(PrimitiveType.Cube);
obj.transform.rotation = q2;

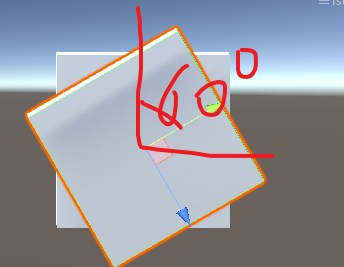
(1,0,0)是从屏幕指向屏幕外

绕x轴转的话，逆着x轴看是顺时针

四元数和欧拉角相互转化

Euler静态方法把欧拉角转成四元数

Euler静态方法用于将欧拉角转换为四元数。

//返回一个旋转，它围绕 z 轴旋转 z 度、围绕 x 轴旋转 x 度、围绕 y 轴旋转 y 度（按该顺序应用）。
//直接传入欧拉角xyz轴旋转的角度即可
Quaternion q3 = Quaternion.Euler(60, 0, 0);
GameObject obj2 = GameObject.CreatePrimitive(PrimitiveType.Cube);
obj2.transform.rotation = q3;

eulerAngles变量把四元数转成欧拉角

eulerAngles变量用于获取或设置四元数的欧拉角表示。

//返回或设置旋转的欧拉角表示。
Quaternion q4 = Quaternion.Euler(60, 0, 0);
print(q4.eulerAngles);//(60.0, 0.0, 0.0)

四元数弥补的欧拉角缺点

注意：一个四元数a乘了另一个四元数b,a按照四元数b旋转了

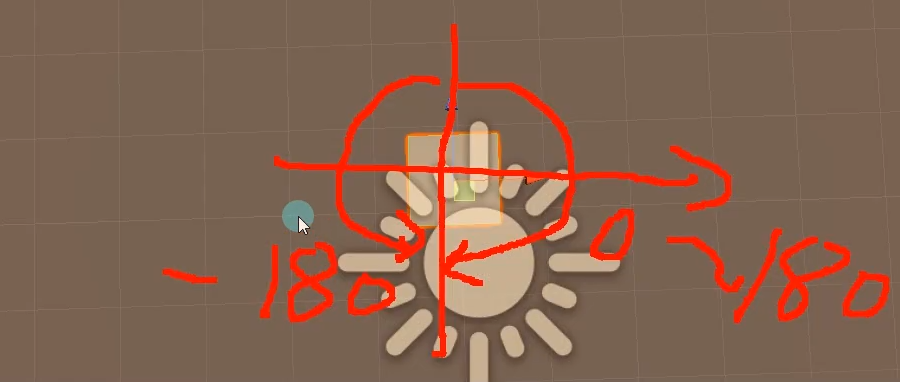
四元数的取值始终是在-180到180之间，旋转表示唯一

把示例立方体x轴旋转90度造成万向节死锁

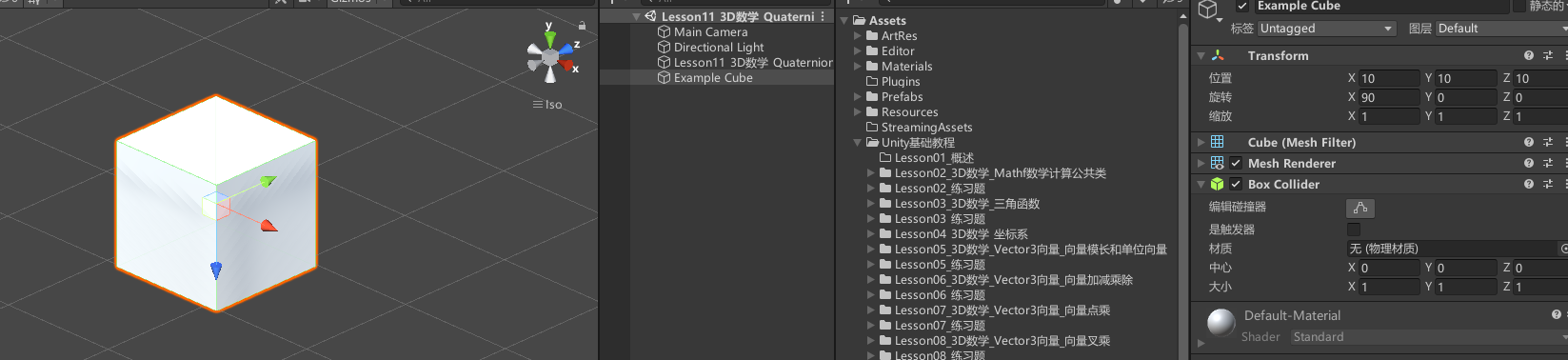
四元数旋转不会造成万向节死锁

//*=四元数就代表绕着四元数的轴旋转度数了
//每一帧绕着y轴旋转1度
exampleCube.transform.rotation *= Quaternion.AngleAxis(1, Vector3.up);//四元数绕y轴转
//就算把示例立方体x轴旋转90度造成万向节死锁 也可以绕着自身的y轴顺时针转
//注意： 这里虽然传入Vector3.up，但是还是以本地坐标系计算

欧拉角造成万向节死锁

//欧拉角添加y轴或z轴旋转都只能绕z轴旋转 会造成万向节死锁
Vector3 eulerAngles;
eulerAngles = exampleCube.transform.rotation.eulerAngles;
//eulerAngles += Vector3.up;//想欧拉角绕y轴转 但还是绕着z轴转
eulerAngles += Vector3.forward;//欧拉角绕z轴转
//转的欧拉角返回成四元数赋值给示例立方体
exampleCube.transform.rotation = Quaternion.Euler(eulerAngles);

总结

11.2 知识点代码

using System.Collections;
using System.Collections.Generic;
using UnityEngine;

public class Lesson11_3D数学_Quaternion四元数_四元数是什么 : MonoBehaviour
{
    public GameObject exampleCube;
    
    void Start()
    {
        #region 知识点一 Unity中的四元数 Quaternion

        //四元数由一个向量(x,y,z)和要旋转的角度β通过数学运算构成 如下
        //四元数Q = [cos(β/2),  sin(β/2)x, sin(β/2)y, sin(β/2)z]

        //Quaternion的构造函数初始化四元数
        //用四元数的计算原理 绕着(x,y,z)向量旋转β度 要传入弧度制 角度转弧度
        //Quaternion q = new Quaternion(Mathf.Sin(β/2 * Mathf.Deg2Rad)*x, Mathf.Sin(β/2 * Mathf.Deg2Rad)*y, Mathf.Sin(β/2 * Mathf.Deg2Rad)*z, Mathf.Cos(β/2 * Mathf.Deg2Rad));
        //绕着(1,0,0)向量旋转60度 要传入弧度制 角度转弧度
        Quaternion q1 = new Quaternion(Mathf.Sin(30 * Mathf.Deg2Rad), 0, 0, Mathf.Cos(30 * Mathf.Deg2Rad));


        //AngleAxis静态方法 绕着某一个向量旋转多少度 返回一个四元数
        //创建一个围绕 axis 旋转 offsetAngle 度的旋转。
        //提供的轴角对 初始化 四元数的方法 分别传入度数和向量轴
        Quaternion q2 = Quaternion.AngleAxis(60, Vector3.right);

        //创建一个立方体演示
        GameObject obj = GameObject.CreatePrimitive(PrimitiveType.Cube);
        obj.transform.rotation = q2;

        #endregion

        #region 知识点二 四元数和欧拉角转换

        //Euler静态方法 把欧拉角转成四元数
        //返回一个旋转，它围绕 z 轴旋转 z 度、围绕 x 轴旋转 x 度、围绕 y 轴旋转 y 度（按该顺序应用）。
        //直接传入欧拉角xyz轴旋转的角度即可
        Quaternion q3 = Quaternion.Euler(60, 0, 0);
        GameObject obj2 = GameObject.CreatePrimitive(PrimitiveType.Cube);
        obj2.transform.rotation = q3;

        //eulerAngles变量 把四元数转成欧拉角
        //返回或设置旋转的欧拉角表示。
        Quaternion q4 = Quaternion.Euler(60, 0, 0);
        print(q4.eulerAngles);//(60.0, 0.0, 0.0)

        #endregion

    }
    
    void Update()
    {
        #region 知识点三 四元数弥补的欧拉角缺点

        //1.同一旋转的表示不唯一  四元数旋转后 转换后的欧拉角 始终是 -180~180度
        //2.万向节死锁 通过四元数旋转对象可以避免万向节死锁

        //把示例立方体x轴旋转90度造成万向节死锁

        //四元数旋转不会造成万向节死锁
        //*=四元数就代表绕着四元数的轴旋转度数了
        //每一帧绕着y轴旋转1度
        exampleCube.transform.rotation *= Quaternion.AngleAxis(1, Vector3.up);//四元数绕y轴转
        //就算把示例立方体x轴旋转90度造成万向节死锁 也可以绕着自身的y轴转
        //注意： 这里虽然传入Vector3.up，但是还是以本地坐标系计算


        //欧拉角添加y轴或z轴旋转都只能绕z轴旋转 会造成万向节死锁
        Vector3 eulerAngles;
        eulerAngles = exampleCube.transform.rotation.eulerAngles;
        //eulerAngles += Vector3.up;//想欧拉角绕y轴转 但还是绕着z轴转
        eulerAngles += Vector3.forward;//欧拉角绕z轴转
        //转的欧拉角返回成四元数赋值给示例立方体
        exampleCube.transform.rotation = Quaternion.Euler(eulerAngles);

        #endregion


    }
}

转载请注明来源，欢迎对文章中的引用来源进行考证，欢迎指出任何有错误或不够清晰的表达。可以在下面评论区评论，也可以邮件至 785293209@qq.com