1.概述
1.1 基础知识
十大排序简介
1. 冒泡排序(Bubble Sort)
冒泡排序是一种简单直观的排序算法,它重复地遍历待排序的元素,比较相邻的两个元素,将较大的元素交换到右侧。时间复杂度为 O(n^2),空间复杂度为 O(1)。
2. 选择排序(Selection Sort)
选择排序是一种简单直观的排序算法,每次选择未排序部分的最小元素,并将其放置在已排序部分的末尾。时间复杂度为 O(n^2),空间复杂度为 O(1)。
3. 插入排序(Insertion Sort)
插入排序是一种简单直观的排序算法,将待排序数组分为已排序和未排序两部分,每次将未排序部分的第一个元素插入到已排序部分的合适位置。时间复杂度为 O(n^2),空间复杂度为 O(1)。
4. 希尔排序(Shell Sort)
希尔排序是一种改进的插入排序算法,通过比较距离较远的元素进行交换,最终使得数组基本有序,然后再使用插入排序对基本有序的数组进行排序。时间复杂度取决于间隔序列的选择,一般为 O(n log n) 到 O(n^2),空间复杂度为 O(1)。
5. 归并排序(Merge Sort)
归并排序是一种分治算法,将待排序数组分成两个子数组,分别排序,然后合并成一个有序数组。时间复杂度稳定在 O(n log n),空间复杂度为 O(n)。
6. 快速排序(Quick Sort)
快速排序是一种分治算法,选择一个基准元素,将小于基准的元素放在左侧,大于基准的元素放在右侧,然后对左右两部分递归地进行排序。时间复杂度平均为 O(n log n),最坏情况为 O(n^2),空间复杂度为 O(log n)。
7. 堆排序(Heap Sort)
堆排序利用了堆这种数据结构,首先将待排序数组构建成一个最大堆,然后依次将堆顶元素与堆末元素交换并调整堆,直到整个数组有序。时间复杂度稳定在 O(n log n),空间复杂度为 O(1)。
8. 计数排序(Counting Sort)
计数排序是一种非比较排序算法,适用于一定范围内的整数排序,它统计每个元素的个数,然后根据统计信息对元素进行排序。时间复杂度为 O(n+k),其中 k 为最大元素与最小元素的差值,空间复杂度为 O(n+k)。
9. 桶排序(Bucket Sort)
桶排序是一种排序算法,它假设输入是由一个随机过程产生,将元素分布在一定范围内的桶中,然后对每个桶中的元素进行排序,最后按照顺序将所有桶中的元素合并。时间复杂度取决于桶的个数和每个桶内部的排序算法,通常为 O(n+k),其中 k 为桶的个数,空间复杂度为 O(n+k)。
10. 基数排序(Radix Sort)
基数排序是一种非比较排序算法,将整数按位数切割成不同的数字,然后按每个位数分别比较进行排序。时间复杂度稳定在 O(d*(n+k)),其中 d 为最大位数,k 为基数,空间复杂度为 O(n+k)。
算法属性表
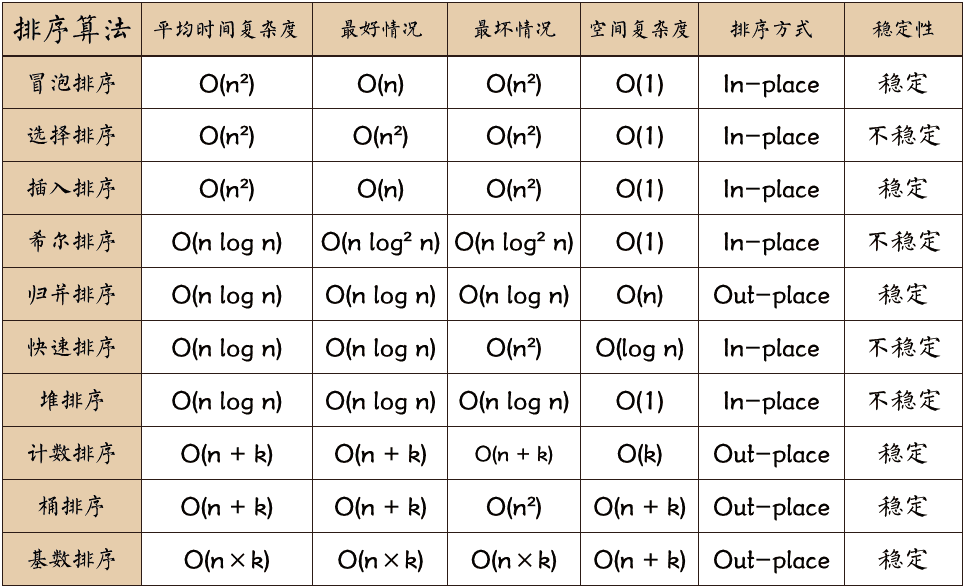
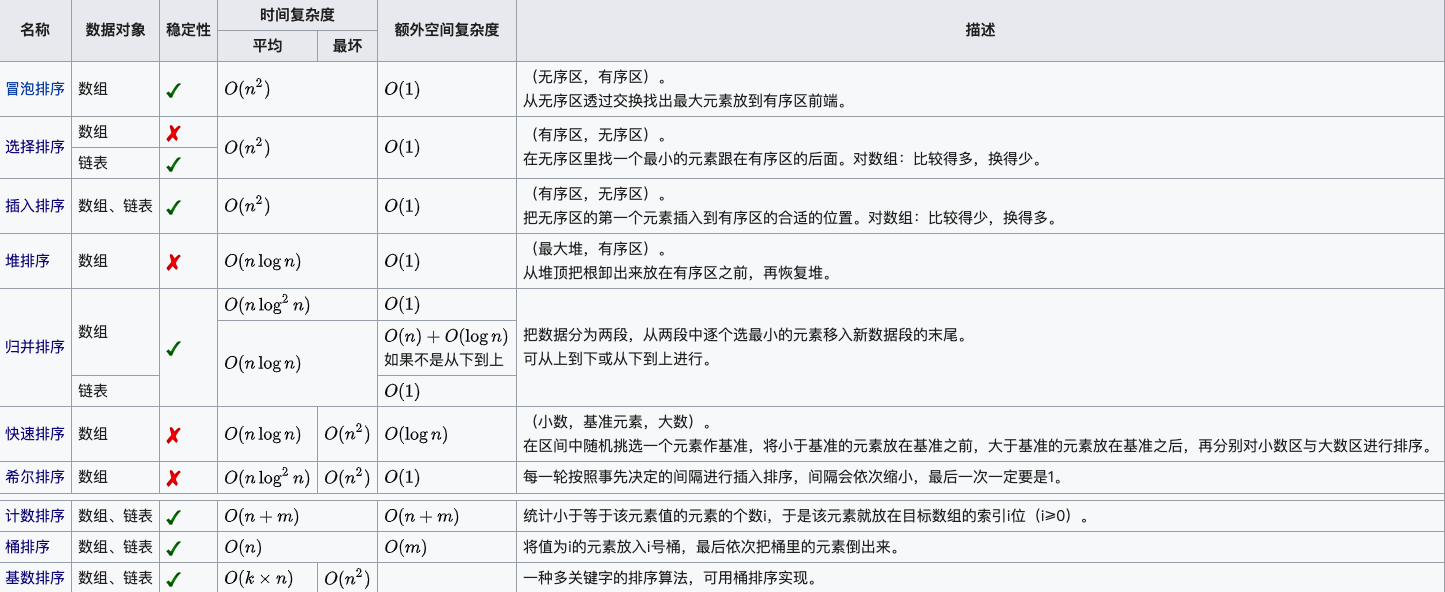
为了方便,演示排序算法时都以从小到大排序作为例子
1.2 算法辅助类
namespace Lesson01_概述;
//提供各个排序都可能要用到的成员
public static class SortHelpTool
{
// 待排序的数组
public static int[] arrayToSort = { 5, 2, 8, 1, 7, 3, 10, 4, 6, 9 };
// 输出数组元素
public static void PrintArray(int[] array)
{
foreach (var item in array)
{
Console.Write(item + " ");
}
Console.WriteLine();
}
// 输出List元素
public static void PrintList(List<int> array)
{
foreach (var item in array)
{
Console.Write(item + " ");
}
Console.WriteLine();
}
// 交换两个元素的值
public static void Swap(ref int a, ref int b)
{
int temp = a;
a = b;
b = temp;
}
// 找到数组中的最大值
public static int FindMaxValue(int[] array)
{
int max = array[0];
foreach (var num in array)
{
if (num > max)
{
max = num;
}
}
return max;
}
// 获取数字的指定位数的值 比如 数1234 第2位数 就是3
public static int GetDigit(int number, int digit)
{
return (number / (int)Math.Pow(10, digit - 1)) % 10;
}
// 计算数字的位数 比如 数1234 就有4位数
public static int CountDigits(int number)
{
return (int)Math.Floor(Math.Log10(number) + 1);
}
}
SortHelpTool = {}
SortHelpTool.arrayToSort = { 5, 2, 8, 1, 7, 3, 10, 4, 6, 9 }
function SortHelpTool.PrintArray(array, str)
print(str .. "\t", table.concat(array, " "))
end
function SortHelpTool.Swap(array, i, j)
temp = array[i]
array[i] = array[j]
array[j] = temp
end
function SortHelpTool.FindMaxValue(array)
local max = array[1]
for i = 2, #array do
if array[i] > max then
max = array[i]
end
end
return max
end
function SortHelpTool.GetDigit(number, digit)
return math.floor(number / 10^(digit - 1)) % 10
end
function SortHelpTool.CountDigits(number)
return math.floor(math.log10(number)) + 1
end
转载请注明来源,欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。可以在下面评论区评论,也可以邮件至 785293209@qq.com

