5.游戏渲染中光和材质的数学魔法
5.1 渲染计算的参与者
光照(Lighting)
光子的发射、反弹、吸收和感知是渲染中一切现象的起源
材质(Material)
物质如何与光子相互作用
着色器(Shader)
如何训练和组织那些”微观奴隶”(计算单元)来完成光子与材质之间庞大而复杂的计算工作

5.2 渲染方程及挑战
渲染方程
渲染方程概述
渲染的本质是求解光与材质相互作用的方程。
1986年,James Kajiya提出了著名的渲染方程(The Rendering Equation),这一方程成为了整个计算机图形学领域的理论基础:
$$L_o\left(x,\omega_o\right)=L_e\left(x,\omega_o\right)+\int_{H^2} f_r\left(x,\omega_o,\omega_i\right) L_i\left(x,\omega_i\right)\cos\theta_i d\omega_i$$

渲染方程可以解读为一句优雅的陈述:
你在一个点上看到的光($L_o$),是它自己发出的光($L_e$),加上来自环境中所有方向的光($L_i$),经过表面材质反射($f_r$)并考虑角度后($\cosθ_i$),最终进入你眼睛的那部分光的总和($\int_{H^2}…dω_i$)。
渲染方程奠定了现代逼真计算机图形绘制的数学基石。简单来说渲染方程是“计算一个点看起来有多亮”的过程:看到的亮度 = 自己发出的光 + 来自环境中所有方向的光经过表面反射后进入眼睛的光的总和。
渲染方程的组成
渲染方程以一种简洁而完备的数学形式,定义了光在场景中传播的物理规律。

方程中的每个部分都有其明确的物理意义:
| 公式部分 | 英文术语 | 中文术语与解释 |
|---|---|---|
| $L_o(x, ω_o)$ | Outgoing / Observed Radiance | 出射辐射度:这是我们最终计算的值,即人眼或摄像机在 $ω_o$ 方向观察点 $x$ 所接收到的总光能。 |
| $L_e(x, ω_o)$ | Emitted Radiance | 自发光辐射度:表示点 $x$ 自身在 $ω_o$ 方向发出的光能(例如灯泡、火焰)。 |
| $\int_{H^2}$ | Integral over Hemisphere | 半球积分:符号表示对以点 $x$ 法线为轴的整个上半球空间(H²)内所有可能的入射方向进行累加求和。这是模拟光线来自四面八方的关键。 |
| $f_r(x, ω_o, ω_i)$ | Scattering Function (BRDF) | 散射函数(双向反射分布函数):描述表面材质属性。它定义了从入射方向 $ω_i$ 来的光,有多少会被反射到出射方向 $ω_o$。 |
| $L_i(x, ω_i)$ | Incoming Radiance | 入射辐射度:从 $ω_i$ 方向照射到点 $x$ 的光线能量。它可能直接来自光源,或从其他物体表面反射而来。 |
| $\cosθ_i$ | Angle between incoming direction and normal | 余弦项:$θ_i$ 是入射光与法线的夹角。$\cosθ_i$ 模拟了光线倾斜照射时能量衰减的几何关系(即“斜射照度低”)。 |
| $dω_i$ | Differential Solid Angle | 微分立体角:代表一个无限小的入射方向范围,是积分计算的基本单位。 |
渲染面临挑战
光照亮了哪些区域以及复杂光源处理
如何准确判断哪些区域被遮挡,无法接收直接光照以及可能产生的阴影。同时还要高效处理各种类型的光源(平行光、点光源、聚光灯、面光源)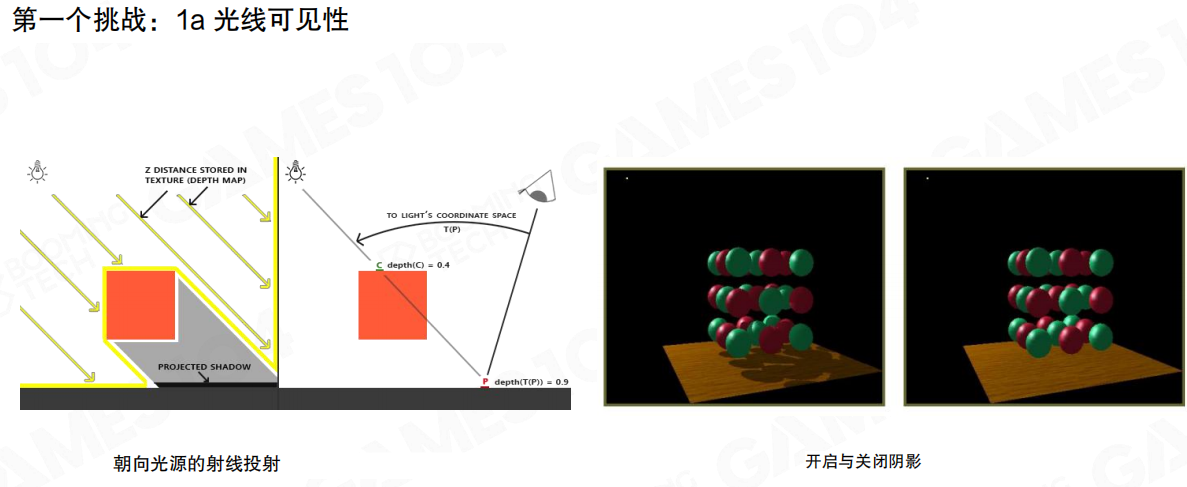
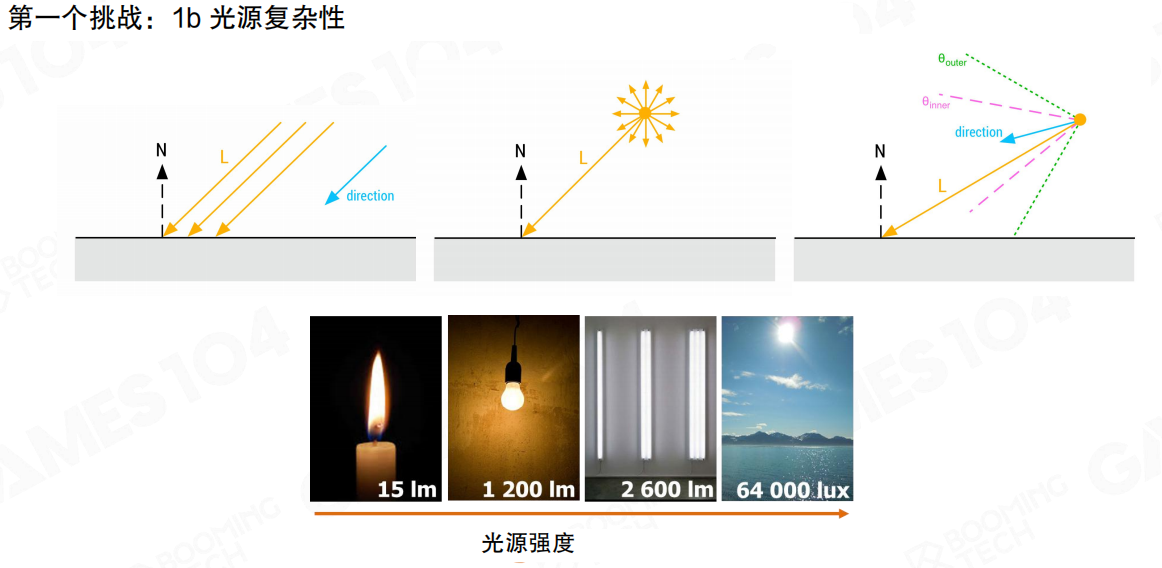
硬件上高效进行积分
渲染方程其涉及了积分计算,十分复杂耗时,在工程实践中如何高效使用是个难题
任何物质都可能成为光源
如何模拟光线在场景中的多次反弹,实现真实的间接光照效果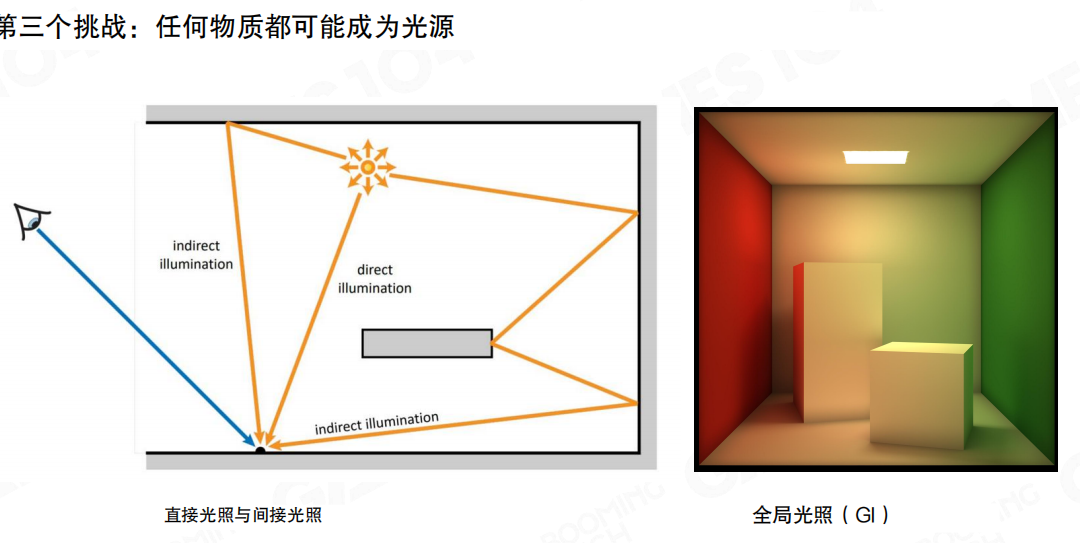
三个主要挑战总结

- 第一个挑战:准确判断哪些区域被遮挡,无法接收直接光照以及可能产生的阴影。同时还要高效处理各种类型的光源(平行光、点光源、聚光灯、面光源)
- 第二个挑战:在半球面上对光照和散射函数进行积分的计算成本高昂
- 第三个挑战:为评估入射辐亮度,我们必须计算另一个积分,即渲染方程是递归的
5.3 基础光照解决方案
暂且抛开一些抽象概念,比如辐射度、微表面和双向反射分布函数等。
简化光源模型
考虑对光照进行分解,将光照效果主要分为三个部分:主光源、环境光和环境贴图。这样已经可以实现一些简单的渲染效果。
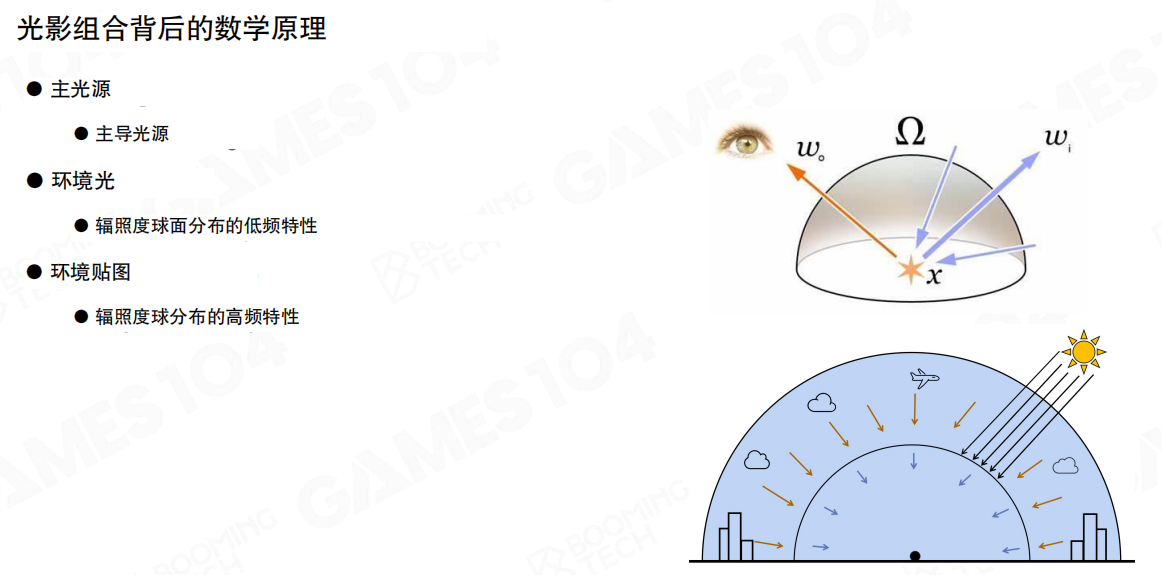
常见的简化光源类型包括:
| 光源类型 | 模拟对象 | 特点 |
|---|---|---|
| 方向光 | 太阳等无限远光源 | 光线平行,强度不随距离衰减 |
| 点光源 | 灯泡等点状光源 | 向所有方向均匀照射,强度随距离衰减 |
| 聚光灯 | 手电筒、舞台灯 | 光线呈锥形,有特定照射方向和范围 |
| 环境光 | 场景中的间接光照 | 无方向,为整个场景提供均匀的基础亮度 |
方向光因其计算简单且能模拟主要日光效果而被广泛使用;点光源和聚光灯则用于营造局部照明效果;而环境光则用一个常量来近似模拟复杂的全局间接光照,虽不精确但能有效避免阴影区域完全漆黑,是一种性能与效果间的实用权衡。
// OpenGL 中的传统光照设置
// 设置第0号光源(GL_LIGHT0)的环境光(Ambient Light)属性。
// 环境光是一种非方向性的背景光,它模拟光线在场景中多次散射后形成的均匀光照,能使背光面不至于完全黑暗。
// 参数 `light_ambient` 是一个包含四个浮点数的数组(RGBA),表示环境光的颜色和强度。例如,{0.2, 0.2, 0.2, 1.0} 表示较弱的白色环境光[1](@ref)。
glLightfv(GL_LIGHT0, GL_AMBIENT, light_ambient);
// 设置第0号光源的漫反射光(Diffuse Light)属性。
// 漫反射光具有方向性,其强度与光线入射方向和表面法线的夹角余弦(即夹角大小)成正比,这是形成物体基本明暗和颜色的主要光源。
// 参数 `light_diffuse` 同样是一个RGBA数组,通常设置为光源的本色,例如 {1.0, 1.0, 1.0, 1.0} 表示白色漫反射光[1,4](@ref)。
glLightfv(GL_LIGHT0, GL_DIFFUSE, light_diffuse);
// 设置第0号光源的镜面反射光(Specular Light)属性。
// 镜面反射光在光滑物体表面形成高光点,其强度与观察方向密切相关,观察方向越接近光线的反射方向,高光越亮。
// 参数 `light_specular` 通常设置为高光颜色,对于模拟白光,常使用 {1.0, 1.0, 1.0, 1.0}[1,4](@ref)。
glLightfv(GL_LIGHT0, GL_SPECULAR, light_specular);
// 设置第0号光源的位置(或方向)。
// 参数 `light_position` 是一个包含四个浮点数(x, y, z, w)的数组,它定义的是齐次坐标。
// - 如果 w = 0,则表示这是一个**定向光**(平行光),如太阳光。此时 (x, y, z) 表示光线的方向矢量,光线无限远且无衰减[4,6](@ref)。
// - 如果 w = 1,则表示这是一个**定位光**(点光源),如灯泡。此时 (x, y, z) 表示光源在空间中的具体位置,其光照强度会根据距离发生衰减[4,6](@ref)。
glLightfv(GL_LIGHT0, GL_POSITION, light_position);

为了模拟金属等光滑表面的镜面反射效果,即让其能映照出周围环境,图形学中常使用环境贴图技术。该技术将整个环境的光照信息预先烘焙在一张立方体贴图中。在着色计算时,只需根据表面的反射方向对这张贴图进行采样,即可高效地获取环境入射光,从而呈现出逼真的反射效果。
void main() {
// 将法向量归一化,确保长度为1,这是光照计算中的标准步骤
// 这里的normal通常是顶点着色器传递过来并经过插值的法线
vec3 N = normalize(normal);
// 计算从表面点指向相机的视线方向向量
// camera_position是相机在世界坐标系中的位置
// world_position是当前片元在世界坐标系中的位置
vec3 V = normalize(camera_position - world_position);
// 计算反射方向:入射光方向(-V)相对于法线N的反射方向
// reflect是GLSL内置函数,参数顺序为(入射方向, 法线)
// 注意:入射方向指向表面,所以需要对视线方向V取反
vec3 R = reflect(-V, N);
// 使用反射方向向量R作为纹理坐标采样立方体贴图
// cube_texture是预先准备好的环境立方体贴图
// 采样结果就是该点应该反射的环境颜色
FragColor = texture(cube_texture, R);
}

简化着色:Blinn-Phong 材质模型
Blinn-Phong 模型将材质反射分解为三个部分:
- 环境光(Ambient):物体某些点不会被光线直接照到,但我们仍然能够看到颜色,这部分区域是通过周围环境的漫反射获得的光照。通常会使用一个固定常量。
- 漫反射(Diffuse):粗糙物体表面向各个方向反射光线(视线与法线的夹角)。
- 高光反射(Specular):光线的镜面反射。
// 设置材质环境光
glMaterialfv(GL_FRONT_AND_BACK, GL_AMBIENT, Ka);
// 设置材质漫反射
glMaterialfv(GL_FRONT_AND_BACK, GL_DIFFUSE, Kd);
// 设置材质高光
glMaterialfv(GL_FRONT_AND_BACK, GL_SPECULAR, Ks);
$$L_{o}\left(x,\omega_{o}\right)=\int_{H^{2}}f_{r}\left(x,\omega_{o},\omega_{i}\right) L_{i}\left(x,\omega_{i}\right)\cos\theta_{i} d\omega_{i}$$

虽然 Blinn-Phong 模型简单高效,但它存在能量不守恒的问题(射入<射出),如果需要做多次漫反射计算时,迭代的颜色可能会越来越亮(不收敛)。而且在光线追踪中表现不稳定,难以模拟复杂的真实材质。

简化阴影:ShadowMap
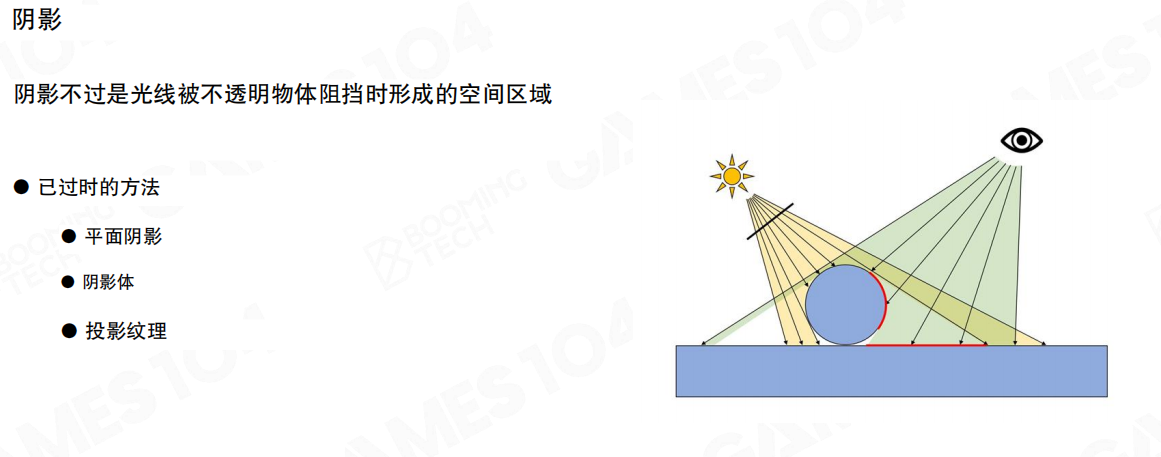
Shadow Mapping 是游戏引擎中最主流的阴影技术:
- 从光源视角渲染深度图(Shadow Map)
- 从相机视角渲染时,将像素点转换到光源空间
- 比较深度值判断是否在阴影中
通俗易懂的说:ShadowMap 技术就是让光源先“看”一次场景,记下“谁离我最近”;然后当摄像机正常渲染时,对于每一个点,都去问光源:“在当前点的那个方向,你记录的最近距离,和这个点的实际距离一样吗?”如果不一样,就说明这个点被更近的东西挡住了,它在阴影里。
// 将3D位置投影到阴影贴图
vec4 proj_pos = shadow_viewproj * pos;
// 从齐次空间到裁剪空间
vec2 shadow_uv = proj_pos.xy / proj_pos.w;
// 从裁剪空间到UV空间
shadow_uv = shadow_uv * 0.5 + vec2(0.5);
// 获取点深度(从-1到1)
float real_depth = proj_pos.z / proj_pos.w;
// 归一化从[-1..+1]到[0..+1]
real_depth = real_depth * 0.5 + 0.5;
// 从深度缓冲区读取深度(在[0..+1]范围内)
float shadow_depth = texture(shadowmap, shadow_uv).x;
// 通过比较计算最终阴影因子
float shadow_factor = 1.0;
if (shadow_depth < real_depth)
shadow_factor = 0.0;
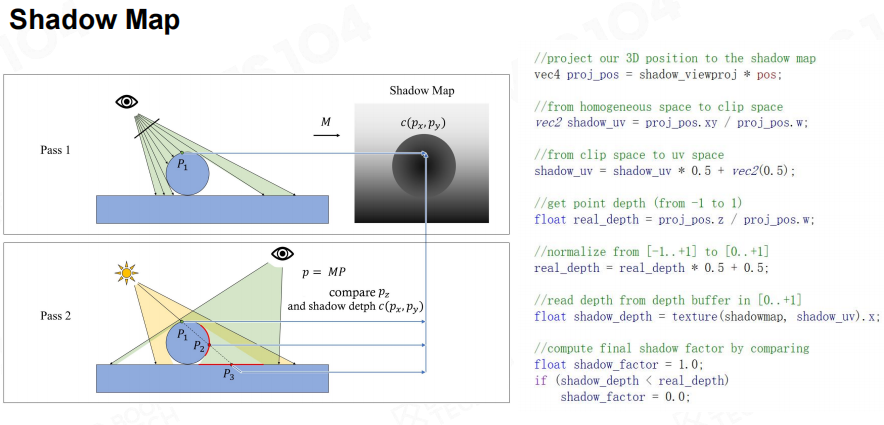
ShadowMap虽然易用,但问题也很明显:渲染Camera区域对ShadowMap进行采样,两者精度是不同的,因此很容易出现走样问题。最常见的就是自遮挡问题。

基础光照解决方案总结

5.4 基于预计算的全局光照
为什么全局光照重要
游戏中的光分为直接光照(光线直接照射)和间接光照(物体之间反射),两者合并称为全局光照。
在上述的简易光照方案中,我们使用ambient作为一个均匀的间接光照。这种处理方式很容易让画面出现平面感,因为现实中各个方向的间接光照是不同的。
直接光照包括:光源的直接光照;动态物体提供实时的环境光计算
间接光照包块:光源在物体之间的光线反射;以及环境光照(比如天空)。
全局光照极大地提升了游戏场景的真实感,使光照更加自然。它的难点在于如何表示来自其它物体反射的间接光照以及如何计算光照与材质BRDF的积分(卷积)。


预计算全局光照的数学基础
实时计算全局光照的计算成本过高,因此我们采用预计算的方式,以内存换时间。但如何高效地表示和存储来自各个方向的环境光照信息,是一个关键问题。
我们需要一种方法,能够:
- 压缩存储:将复杂的球面光照信号压缩为少量参数
- 高效计算:在运行时快速重建光照信息
- 支持卷积:便于与材质BRDF进行积分计算
为此,我们需要先了解傅里叶变换和卷积定理,它们是理解球谐函数的基础。
傅里叶变换
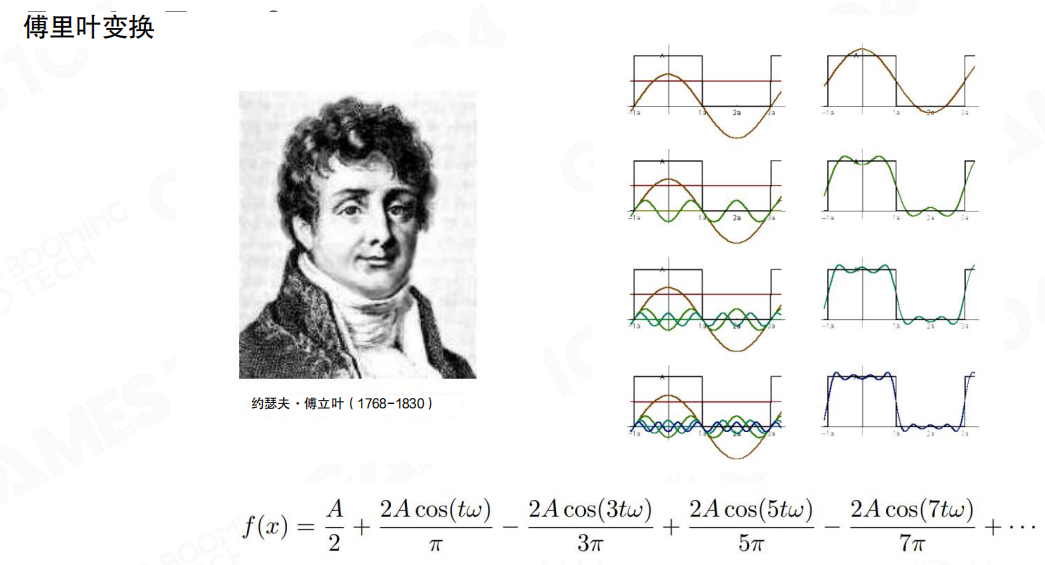
傅里叶变换的核心思想在于:任何复杂的信号(无论是声音、图像还是游戏中的光照),都可以被看作是许多个不同频率、不同强度的“简单波”叠加而成的。
傅里叶变换就像 “成分分析眼镜” 。它让你能看清任何复杂事物(声音、图像、光照)的本质结构。
- 输入:一盘复杂的菜肴(或一束混合光)。
- 输出:一份精确的“成分清单”,告诉你里面包含多少“西红柿”(低频基波)、多少“牛肉”(中频谐波)、多少“辣椒粉”(高频噪声)。
卷积定理
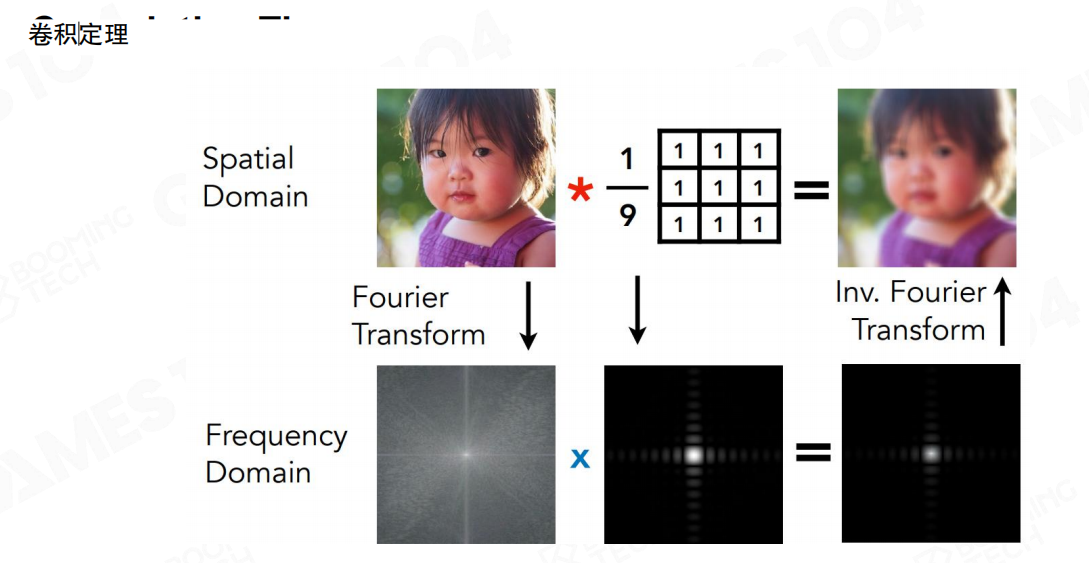
卷积是是什么
卷积描述的是一个系统如何影响一个信号。
一个经典比喻是“回声”:
- 你拍一下手(原始信号)。
- 在山谷中(系统特性),你听到的不仅是拍手声,还有一系列逐渐减弱的回声。
- 你最终听到的声音,就是“拍手声”和“山谷的回声特性”进行卷积的结果。
在图像处理中,“模糊”就是一个典型的卷积操作:
- 原始图片:清晰的图像。
- 系统(卷积核):一个小的矩阵(比如您图2中那个所有值都是1的3x3矩阵,乘以1/9其实就是求平均)。
- 卷积过程:将这个小矩阵在图像上每个像素点滑动,计算周围像素的平均值。这个“滑动求平均”的过程就是卷积。
- 结果:得到一张模糊的图片。
直接计算卷积在数学上很复杂,计算量巨大。所以引出了卷积定理
应用卷积定理
卷积定理指出:在空域中复杂的卷积运算,在频域中等价于简单的乘法运算。
卷积定理的数学表达式为:
$$\mathcal{F}{f * g} = \mathcal{F}{f} \cdot \mathcal{F}{g}$$
其中:
- $f$ 是信号(如原始图像),
- $g$ 是系统(如卷积核或滤波器),
- $*$ 表示卷积操作,
- $\mathcal{F}$ 表示傅里叶变换,
- $\cdot$ 表示乘法。
- $\mathcal{F}{f * g}$ 是卷积结果的傅里叶变换(即 **F(卷积)**),
- $\mathcal{F}{f}$ 是信号的傅里叶变换(即 **F(信号)**),
- $\mathcal{F}{g}$ 是系统的傅里叶变换(即 **F(系统)**)。
这意味着,计算“模糊一张图片”这个复杂任务,有了一个全新的、极其高效的解决方案:
flowchart TD
A[“原始清晰图像
(空域)”] --> B[“傅里叶变换”]
C[“模糊滤镜(卷积核)
(空域)”] --> D[“傅里叶变换”]
B --> E[“图像的频域表示”]
D --> F[“滤镜的频域表示”]
E --> G[频域相乘]
F --> G
G --> H[“模糊结果的频域表示”]
H --> I[傅里叶逆变换]
I --> J[“最终模糊图像
(空域)”]
信号(原始输入):
- 对应节点 “原始清晰图像(空域)”。
- 这是待处理的原始数据,在图像处理中代表输入图像(如一张清晰图片)。
系统(卷积核或滤波器):
- 对应节点 “模糊滤镜(卷积核)(空域)”。
- 这定义了如何修改信号(如图像模糊操作),通常是一个小矩阵(如高斯核),表示系统的响应特性。
F(信号)(信号的傅里叶变换):
- 对应节点 “图像的频域表示”。
- 这是通过傅里叶变换将信号A转换到频域后的结果,表示图像的频率成分。
F(系统)(系统的傅里叶变换):
- 对应节点 “滤镜的频域表示”。
- 这是通过傅里叶变换将系统C转换到频域后的结果,表示滤波器的频率响应。
F(卷积)(卷积结果的傅里叶变换):
- 对应节点 “模糊结果的频域表示”。
- 根据卷积定理,这是 F(信号) × F(系统) 的乘积结果,即节点 “频域相乘” 的输出。它代表了卷积操作(模糊处理)在频域中的等价形式。
最终卷积结果:
- 对应节点 “最终模糊图像(空域)”。
- 这是通过将(F(卷积))进行傅里叶逆变换得到的时域结果,即应用系统(模糊滤镜)后的输出图像。
直接卷积的计算复杂度:在空域中直接计算卷积(尤其是大图像和大卷积核时)需要 ( O(N^2) ) 次操作,非常耗时。
卷积定理的优势:通过傅里叶变换将问题转移到频域,卷积变为简单的乘法(复杂度 ( O(N) )),整体复杂度降至 ( O(N \log N) )(得益于快速傅里叶变换FFT)。这使得实时图像处理(如游戏引擎中的后处理效果)成为可能。
SH球谐函数
有了傅里叶变换和卷积定理的基础,我们现在可以理解球谐函数(Spherical Harmonics, SH)了。球谐函数可以理解为球面上的傅里叶变换——正如傅里叶变换将时域信号分解为不同频率的正弦波,球谐函数将球面上的光照信号分解为一系列相互正交的基函数。
任意球面信号都可以表示为这些基函数的加权和,而且这些基函数具有正交性和旋转不变性等重要特性,这使得球谐函数成为表示环境光照的理想工具。

球谐函数在物理上对应着氢原子轨道的概率分布,在数学上则是一组定义在球面上的正交基函数。通过增加基函数的阶数,我们可以更精确地表示复杂的光照分布。
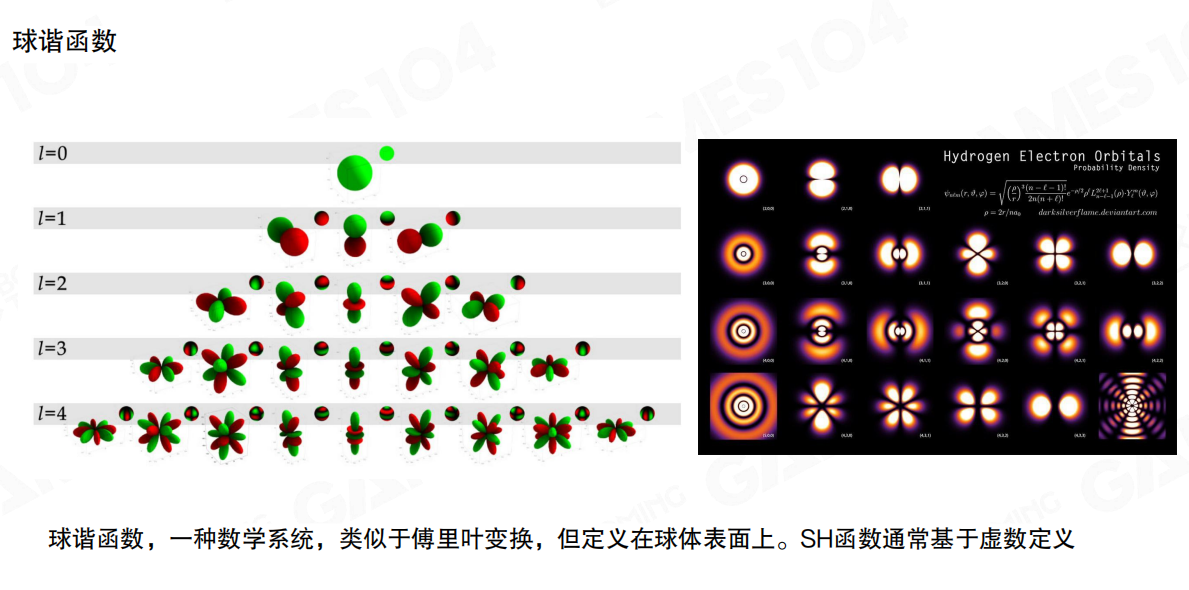

在实时渲染中,我们通常只需要使用1-2阶的低频球谐函数就能实现合理的渲染效果。以2阶SH为例,每个方向的光照信息只需要12个系数(RGB三个通道各4个系数)即可表示。更重要的是,球面上两个函数的卷积可以简化为其SH系数的卷积,这使得光照与材质BRDF的积分计算变得高效。

SH的压缩过程是:首先从环境贴图(如全景图或环境立方体贴图)中采样,然后将其投影到球谐基函数上得到系数,最后在着色器中根据方向重建光照。这种压缩方式能够以极小的存储空间(通常每个采样点只需32位)替代高精度的原始环境贴图数据。

在存储时,我们可以对不同阶的系数使用不同的精度:L0系数使用HDR格式(BC6H纹理),L1系数使用LDR格式(BC7或BC1纹理)。这样,每个点的环境光照可以用RGBA的32位来表示,相当于纹理图像上的一个像素,实现了极高的压缩率。

LightMap光照贴图
实时计算全局光照的计算成本过高,因此我们采用预计算的方式,以内存换时间。最直观的思路是:将场景中每个点的环境光照信息预先计算并存储到一张纹理图上,渲染时只需根据方向进行纹理采样即可获取光照信息,避免实时计算。
这种预计算的光照纹理就是LightMap(光照贴图)。具体实现时,我们将场景的几何体参数化到2D纹理空间,对每个表面点计算其接收到的环境光照(通常使用球谐函数编码),然后将这些光照数据烘焙到纹理的对应像素中。

为了优化烘焙效率,我们通常使用低多边形代理几何体进行烘焙,而不是包含所有细节的高精度网格。烘焙完成后,再将光照贴图投影到所有LOD层级的最终几何体上。

LightMap的渲染流程包括:间接光照计算、直接光照叠加,以及最终的材质着色。通过这种方式,我们可以在运行时高效地渲染出包含丰富光照细节的静态场景。



LightMap的优缺点:
优点:
- 运行时效率极高,只需简单的纹理采样
- 能够烘焙大量精细的光照细节,包括环境光遮蔽等
缺点:
- 离线烘焙过程漫长且计算成本高(通常需要光照贴图农场)
- 仅能处理静态场景和静态光源,无法应对动态变化
- 存储成本较高,对打包体积和GPU内存有较大影响

LightProbe光照探针和ReflectionProbe反射探针
LightMap虽然高效,但只能处理静态物体。当场景中有动态物体(如玩家、NPC、可移动道具)时,我们需要另一种方案:在场景空间中放置光照探针(Light Probe)来记录环境光照信息。
Light Probe是场景空间中的采样点,每个探针会记录其周围的光场信息(通常使用球谐函数编码以节省存储空间)。当动态物体需要着色时,我们只需对附近几个探针的光照数据进行插值,即可估算出该点的环境光照。这种插值通常使用重心坐标或距离加权的方式实现。

探针的生成可以基于地形、道路等场景特征,或通过体素化场景自动生成。现代引擎通常提供自动化工具来生成探针网格,无需美术手动放置。

当需要处理镜面反射时,我们使用反射探针(Reflection Probe)。反射探针的采样密度通常较低,但每个探针需要更高的精度来捕获周围环境的反射信息。

Light Probe + Reflection Probe的优缺点:
优点:
- 运行时效率极高
- 可应用于静态和动态对象
- 能够同时处理漫反射和高光着色
缺点:
- 光照探针需要进行预计算(使用SH编码压缩光场数据)
- 采样率不足导致光照细节不够,无法处理全局光照的精细细节(如重叠结构上的柔和阴影)

基于预计算的全局光照总结
预计算全局光照的核心思路是:既然实时计算全局光照成本过高,那就提前计算并存储结果,运行时直接读取。这是一种典型的”以空间换时间”策略。
预计算的基本思路
就像餐厅提前准备半成品,客人点单时直接烹饪,而不是从采购食材开始。我们提前计算场景中每个点的光照信息并存储,游戏运行时只需查表读取,避免了重复计算。
数学基础:傅里叶变换与卷积定理
傅里叶变换让我们能够将复杂的球面光照信号分解为简单的基函数组合,就像将一首交响乐分解为各个乐器的音符。卷积定理则提供了计算捷径:在频域中,复杂的卷积运算变成了简单的乘法,大大提高了计算效率。
SH球谐函数:高效的压缩工具
球谐函数能够将来自各个方向的光照信息压缩为少量参数。例如,用12个系数就能描述整个球面的光照分布,而不需要存储完整的环境贴图。这就像用”左边亮、右边暗、上方有窗户”这样的描述来概括房间的亮度分布,而不是记录每个角落的具体数值。
LightMap:静态场景的光照烘焙
LightMap将静态场景的光照信息预先计算并烘焙到纹理中。运行时直接采样纹理即可获得光照值,就像查看一张光照快照。这种方法对建筑物、地形等静态场景非常有效,能够提供精细的光照细节,但缺点是场景改动后需要重新烘焙。
LightProbe:动态物体的环境光照
对于动态物体,我们在场景中放置光照探针,每个探针记录周围的光照环境(使用SH压缩存储)。当动态物体移动时,通过插值附近探针的数据来估算当前位置的光照。这类似于天气预报:虽然无法在每个位置都设置气象站,但通过有限站点的数据可以推测其他位置的情况。
总结
预计算全局光照系统通过数学工具(傅里叶变换、卷积定理)提供理论基础,通过SH球谐函数实现高效压缩,通过LightMap处理静态场景,通过LightProbe处理动态物体。虽然每种方法都有其局限性,但组合使用能够实现既真实又高效的渲染效果。
5.5 基于物理的材质
有了全局光照的基础,我们还需要准确描述材质如何与光线相互作用。基于物理的材质(Physically Based Rendering, PBR)模型通过微表面理论来模拟现实世界中材质的反射行为,让渲染结果更加真实。
微表面理论
微表面理论认为,任何看似光滑的物体表面在微观尺度上都是由大量方向各异的小平面(微表面)组成的。这些微表面的法线分布决定了材质的视觉特性。
关键点:微表面法线的分布
当微表面的法线方向较为一致时,光线会朝相似的方向反射,形成清晰的镜面反射,表现为光滑、高光的材质。反之,当微表面法线方向杂乱无章时,光线会朝各个方向散射,形成柔和的漫反射,表现为粗糙、哑光的材质。

高光集中度与光泽度直接相关:法线分布越集中,高光越锐利,材质越光滑;法线分布越分散,高光越柔和,材质越粗糙。
基于微表面理论的BRDF模型
在渲染方程中,我们使用BRDF(双向反射分布函数)来描述材质如何反射光线。基于微表面理论,BRDF可以分解为两个主要部分:漫反射(Diffuse)和高光反射(Specular)。
光线与材质的相互作用
当光线照射到物体表面时,会发生两种不同的反射:
- 体反射(Body Reflection):光线进入物体内部,经过多次散射后从表面的另一个点射出。这对应着漫反射行为,可以使用Lambert模型表示。
- 表面反射(Surface Reflection):光线直接在表面反射,不进入物体内部。这对应着高光反射行为,可以使用基于微表面理论的Cook-Torrance模型表示。

金属与非金属的区别
金属的电子可以捕获光子并将其吸收,因此金属几乎没有漫反射,主要表现为高光反射。非金属则无法捕获光子,进入内部的光线会被散射出来形成漫反射,同时表面也会产生一定的高光反射。
BRDF的数学表达式为:
\[
f_r = k_d \cdot f_{Lambert} + f_{CookTorrance}
\]
其中:
- ( f_{Lambert} = \frac{c}{\pi} ) 表示漫反射项
- ( f_{CookTorrance} = \frac{DFG}{4(\omega_o \cdot n)(\omega_i \cdot n)} ) 表示高光反射项
Cook-Torrance模型的DFG三项
Cook-Torrance模型将高光反射分解为三个相互独立的项:D(法线分布函数)、F(菲涅尔项)和G(几何衰减项)。这三项分别描述了微表面的不同特性。粗糙度(主要影响D项)如何决定高光的大小和形状;金属度(主要影响F项)如何决定反射的强度和颜色;而G项如何模拟表面微观细节的互遮挡效应,让粗糙表面的高光在掠射角会变宽。
D项:法线分布函数(Normal Distribution Function)
法线分布函数描述了微表面法线在不同方向上的分布情况,它决定了高光的形状和大小。
GGX分布
游戏引擎中通常使用GGX(Trowbridge-Reitz)分布函数,它在高频和低频都有更好的效果,能够产生更真实的高光。GGX分布只需要一个粗糙度(roughness)参数,就能描述从镜面反射到漫反射的完整范围。
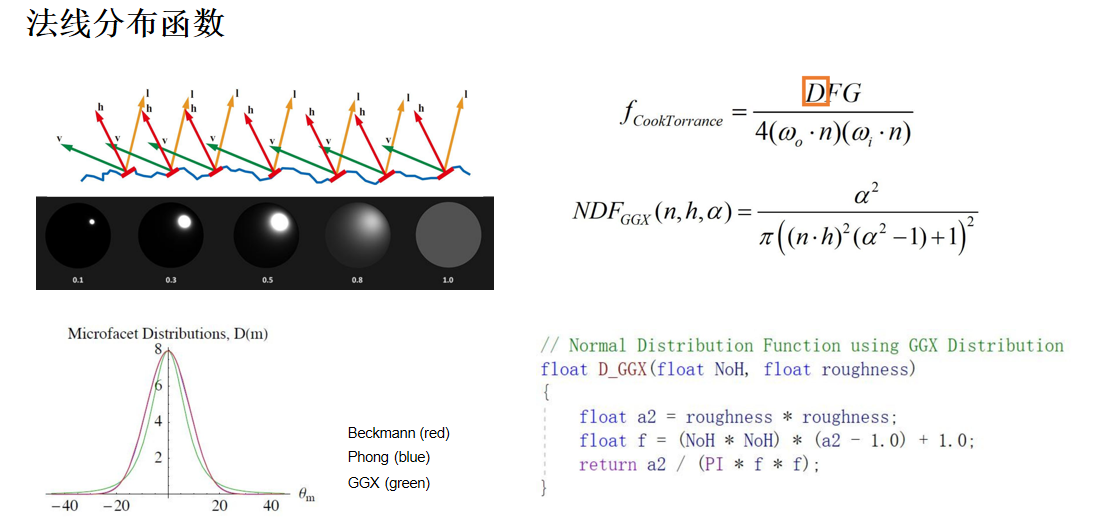
粗糙度越大,微表面法线分布越分散,高光越柔和;粗糙度越小,法线分布越集中,高光越锐利。GGX分布相比传统的Beckmann和Phong分布,具有更尖锐的峰值和更长的尾部,这使得它在掠射角时能产生更真实的高光效果。
G项:几何衰减项(Geometry Attenuation Term)
几何衰减项描述了微表面之间的自遮挡和自阴影效应。当表面粗糙时,某些微表面可能会遮挡其他微表面的反射光线,或者遮挡入射光线,从而减少最终反射到观察者眼中的光量。
Smith模型
Cook-Torrance模型使用Smith模型将几何项分解为入射方向和出射方向两个方向上的可见性乘积:
\[
G_{Smith}(l, v) = G_{GGX}(l) \cdot G_{GGX}(v)
\]
每个方向上的可见性使用GGX模型计算,同样只需要粗糙度参数。
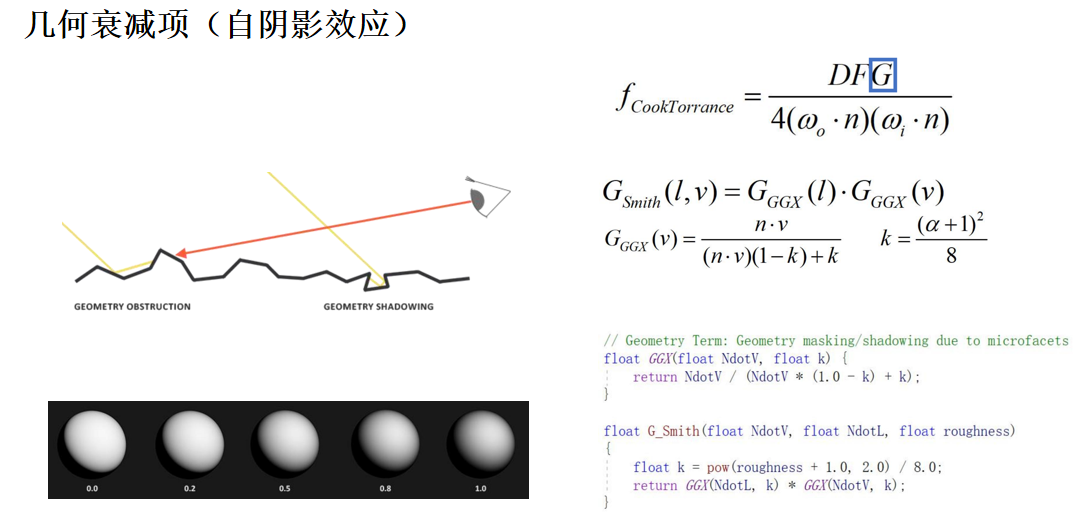
几何遮挡(Geometry Obstruction)和几何阴影(Geometry Shadowing)是微表面理论中重要的物理现象,它们让粗糙表面的反射更加真实。
F项:菲涅尔方程(Fresnel Equation)
菲涅尔方程描述了不同材质在光滑表面上的理想反射行为。它告诉我们:观察角度不同,反射强度也不同。
菲涅尔效应
当视线与表面垂直时(法线方向),反射较弱,材质看起来更透明;当视线与表面接近平行时(掠射角),反射很强,材质看起来像镜子。这就是为什么我们在看平静的湖面时,远处的水面像镜子一样反射天空,而近处的水面则能看到水底的石头。

在实时渲染中,通常使用Schlick近似来计算菲涅尔项:
\[
F_{Schlick}(h, v, F_0) = F_0 + (1 - F_0)(1 - (v \cdot h))^5
\]
其中 ( F_0 ) 是材质在垂直入射时的反射率,不同材质有不同的 ( F_0 ) 值。
MERL BRDF数据库
虽然Cook-Torrance模型已经能够很好地表达物理世界的效果,但现实中的材质仍然非常复杂。为了获得真实材质的光学参数,我们需要进行实际的物理测量。
BRDF测量
MERL BRDF数据库使用专门的测角反射计(Gonioreflectometer)对大量真实材质进行采样,精确测量不同入射角和观察角下的反射行为,提供了81种常见材质的BRDF测量数据。

这些实测数据为艺术家和程序员提供了准确的材质参数参考,避免了手动调参的困难,让材质渲染更加真实。
Disney Principled BRDF
为了方便不同背景的从业者使用,迪士尼动画工作室的Brent Burley提出了Disney Principled BRDF。它的核心思想是:设计材质模型时要尽可能方便艺术家理解,而不是过多使用物理概念。
设计原则
Disney Principled BRDF遵循以下原则:
- 应采用直观而非物理参数
- 参数数量应尽可能少
- 参数在其合理范围内应设置为0到1之间的值
- 参数应允许在合理范围内突破其可信区间
- 所有参数组合都应尽可能保持鲁棒性与物理合理性

材质参数
Disney Principled BRDF提供了10个直观的材质参数,每个参数都有明确的视觉效果:

- subsurface:次表面散射,模拟光线在材质内部的传播
- metallic:金属度,控制材质是金属还是非金属
- specular:高光强度
- specularTint:高光色调
- roughness:粗糙度,控制表面的光滑程度
- anisotropic:各向异性,模拟拉丝金属等材质
- sheen:光泽,模拟织物等材质的边缘高光
- sheenTint:光泽色调
- clearcoat:清漆层,模拟汽车漆等多层材质
- clearcoatGloss:清漆光泽度
PBR Specular-Glossiness工作流
基于上述理论,现代游戏引擎中常用的PBR材质模型主要有两种工作流。首先是Specular-Glossiness(SG)工作流。
BRDF实现
SG工作流将材质属性分解为三张纹理图:Diffuse(漫反射颜色)、Specular(高光颜色,即F0值)、Glossiness(光泽度,与粗糙度相反)。在着色器中,我们通过采样这些纹理并计算BRDF来渲染材质。

BRDF计算包括:
- 漫反射项:使用Lambert模型
- 高光项:使用Cook-Torrance模型,计算D、F、G三项
- 最终颜色:漫反射和高光的叠加
材质效果
SG工作流能够精确控制材质的各个方面,特别是可以通过Specular贴图直接控制电介质的F0值,这对于需要精确控制反射的材质非常有用。

在SG模型中,金属部分的Diffuse为黑色(金属无漫反射),Specular为金属颜色;非金属部分的Diffuse为材质颜色,Specular为电介质的F0值(通常为2-5%的灰色)。
PBR Metallic-Roughness工作流
虽然SG工作流非常灵活,但Specular贴图有RGB三个参数,灵活的另一面是难以控制,容易出错。因此,Metallic-Roughness(MR)工作流应运而生。
MR模型
MR工作流同样使用三张纹理图:Base Color(基础颜色)、Roughness(粗糙度)、Metallic(金属度)。相比SG工作流,MR工作流通过金属度参数来关联漫反射和菲涅尔项,避免了参数冲突问题。
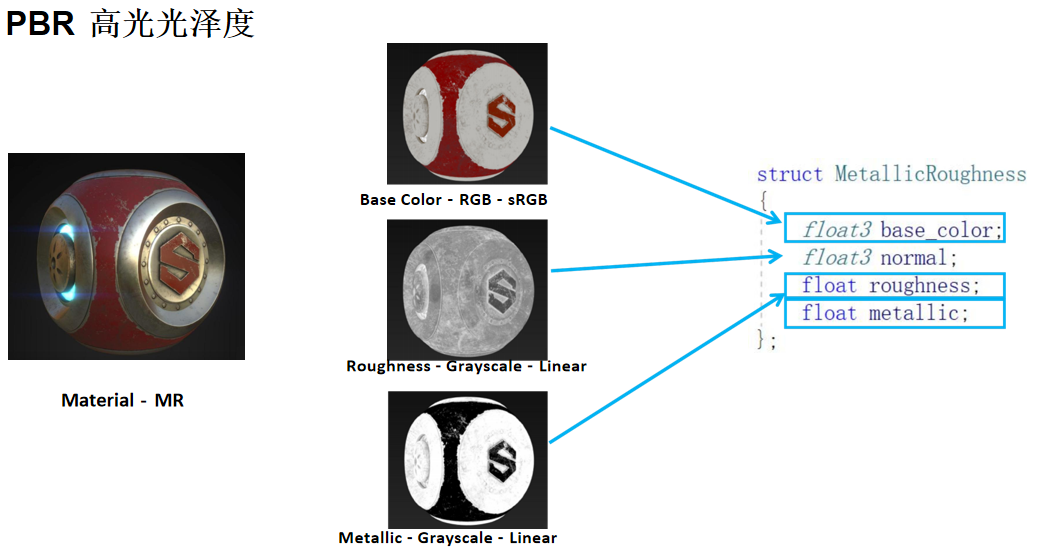
工作原理
- 当Metallic = 0(非金属)时:Base Color作为漫反射颜色,F0使用默认的电介质值(通常为4%)
- 当Metallic = 1(金属)时:Base Color作为F0值(金属的反射颜色),漫反射为0
本质上,MR材质还是使用SG材质的BRDF计算,只是对参数做了限制,让美术更容易使用且不易出错。
MR与SG的转换和对比
MR和SG两种工作流可以相互转换,核心在于如何处理F0值。
转换方法
从MR转换为SG的公式为:
- Specular =
lerp(dielectricSpecularColor, base_color, metallic)- 非金属:使用电介质的F0值
- 金属:使用base_color
- Diffuse =
base_color - base_color * metallic- 非金属:等于base_color
- 金属:等于0
- Glossiness =
1.0 - roughness

F0值参考
不同材质有不同的F0值。常见电介质的F0值在2%-5%之间(线性值0.02-0.05),例如水为2%,塑料和玻璃为4-5%,宝石为5-8%。这些参考值对于正确设置材质非常重要。
两种工作流的对比

MR工作流的优点:
- 更易于创作,不易因错误的F0数据导致错误
- 减少纹理内存使用(Metallic和Roughness都是灰度图)
MR工作流的缺点:
- 在贴图创建过程中无法直接控制电介质的F0值(大多数实现提供高光控制功能覆盖默认值)
- 边缘伪影更明显,尤其在较低分辨率下
SG工作流的优点:
- 边缘伪影较不明显
- 可以在Specular贴图中精确控制电介质的F0值
SG工作流的缺点:
- 由于Specular贴图提供了对F0值的控制,使用不当更容易出现数值错误,可能违反能量守恒
- 使用更多纹理内存(额外增加一张RGB贴图)
选择建议
大多数情况下,MR工作流是工程中的首选,因为它更简单、更节省内存,且不易出错。但对于需要精确控制F0值或边缘质量要求较高的场景,SG工作流仍然有其优势。
5.6 基于图像的光照(Image-Based Lighting IBL)
有了PBR材质模型,我们还需要解决渲染方程中的积分计算问题。基于图像的光照(Image-Based Lighting, IBL)使用真实的环境图像作为光照源,通过预计算的方式将复杂的积分项提前计算好,实现了既真实又高效的实时渲染。
IBL的基本思想
IBL的核心思想很简单:用一张环境贴图(Environment Map)来表示来自各个方向的远距离光照。这张贴图就像一张全景照片,记录了场景中所有方向的光照信息。
渲染方程的挑战
要计算一个点在环境光照下的颜色,我们需要求解渲染方程:
\[
L_o(x, \omega_o) = \int_{H^2} f_r(x, \omega_o, \omega_i) L_i(x, \omega_i) \cos \theta_i d\omega_i
\]
这个方程需要对半球面上的所有入射方向进行积分。如果使用蒙特卡洛方法进行大量采样来计算这个积分,计算量会非常大,无法满足实时渲染的要求。

IBL的解决方案
IBL采用预计算的方式,提前将积分项计算好并存储起来,运行时直接查表即可。这是一种典型的”以空间换时间”策略,让我们能够在实时渲染中高效地使用环境光照。
BRDF分解回顾
在介绍IBL的具体实现之前,我们先回顾一下BRDF的分解。根据前面的内容,BRDF可以分解为漫反射和高光反射两部分:
\[
f_r = k_d \cdot f_{Lambert} + f_{CookTorrance}
\]
相应地,出射辐射度也可以分解为:
\[
L_o(x, \omega_o) = L_d(x, \omega_o) + L_s(x, \omega_o)
\]
其中:
- ( L_d ) 是漫反射项(Diffuse)
- ( L_s ) 是高光反射项(Specular)

IBL对这两项分别进行处理,然后累加起来得到最终的环境光照效果。这种分离处理的方式让每项都能找到高效的预计算方法。
漫反射辐照度图(Diffuse Irradiance Map)
对于漫反射项,处理相对简单。根据Lambert模型,漫反射BRDF为 ( f_{Lambert} = \frac{c}{\pi} ),因此漫反射辐射度为:
\[
L_d(x, \omega_o) = \int_{H^2} k_d \cdot \frac{c}{\pi} \cdot L_i(x, \omega_i) \cos \theta_i d\omega_i
\]
由于Lambert模型是各向同性的(不依赖观察方向),我们可以将常数项提取出来:
\[
L_d(x, \omega_o) \approx k_d \cdot c \cdot \frac{1}{\pi} \int_{H^2} L_i(x, \omega_i) \cos \theta_i d\omega_i
\]
辐照度项
关键的部分是积分项 ( \frac{1}{\pi} \int_{H^2} L_i(x, \omega_i) \cos \theta_i d\omega_i ),这被称为辐照度(Irradiance)。这个积分只依赖于表面法线方向,不依赖于观察方向,因此我们可以预先计算好并存储在一张纹理中。

辐照度图的生成
辐照度图是对原始环境贴图进行模糊处理得到的。模糊的过程实际上就是在做积分:对每个法线方向,我们计算该方向上所有入射光线的加权平均(权重为余弦项)。结果是一张比原始环境贴图更模糊、更柔和的图像,它直接存储了每个方向的辐照度值。
运行时,我们只需要根据表面法线方向采样这张辐照度图,然后乘以漫反射系数即可,计算非常简单高效。
镜面反射的分离求和近似
高光反射项的处理要复杂得多,因为Cook-Torrance BRDF依赖于观察方向、入射方向和材质参数。直接预计算所有可能的组合是不现实的。
分离求和近似(Split-Sum Approximation)
我们可以将高光反射的积分近似分解为两个独立项的乘积:
\[
L_s(x, \omega_o) = \int_{H^2} f_{CookTorrance} \cdot L_i(x, \omega_i) \cos \theta_i d\omega_i
\]
\[
\approx \frac{\int_{H^2} f_{CookTorrance} \cdot L_i(x, \omega_i) \cos \theta_i d\omega_i}{\int_{H^2} f_{CookTorrance} \cos \theta_i d\omega_i} \cdot \int_{H^2} f_{CookTorrance} \cos \theta_i d\omega_i
\]
虽然乘积的积分与积分的乘积在数学上并不等价,但在实际应用中,这种近似能够产生足够好的视觉效果。

两项的含义
- 光照项(Lighting Term):第一项,描述了环境光照的贡献,依赖于粗糙度
- BRDF项(BRDF Term):第二项,描述了材质BRDF的贡献,依赖于粗糙度和观察角度
这两项可以分别预计算,大大简化了实时计算。
光照项:预过滤环境贴图
光照项需要根据不同的粗糙度值进行预计算。对于每个粗糙度值,我们生成一张对应的预过滤环境贴图(Pre-filtered Environment Map)。
预过滤过程
预过滤的过程实际上是在模拟不同粗糙度下的高光反射。粗糙度越大,高光越分散,对应的环境贴图就越模糊;粗糙度越小,高光越集中,对应的环境贴图就越清晰。
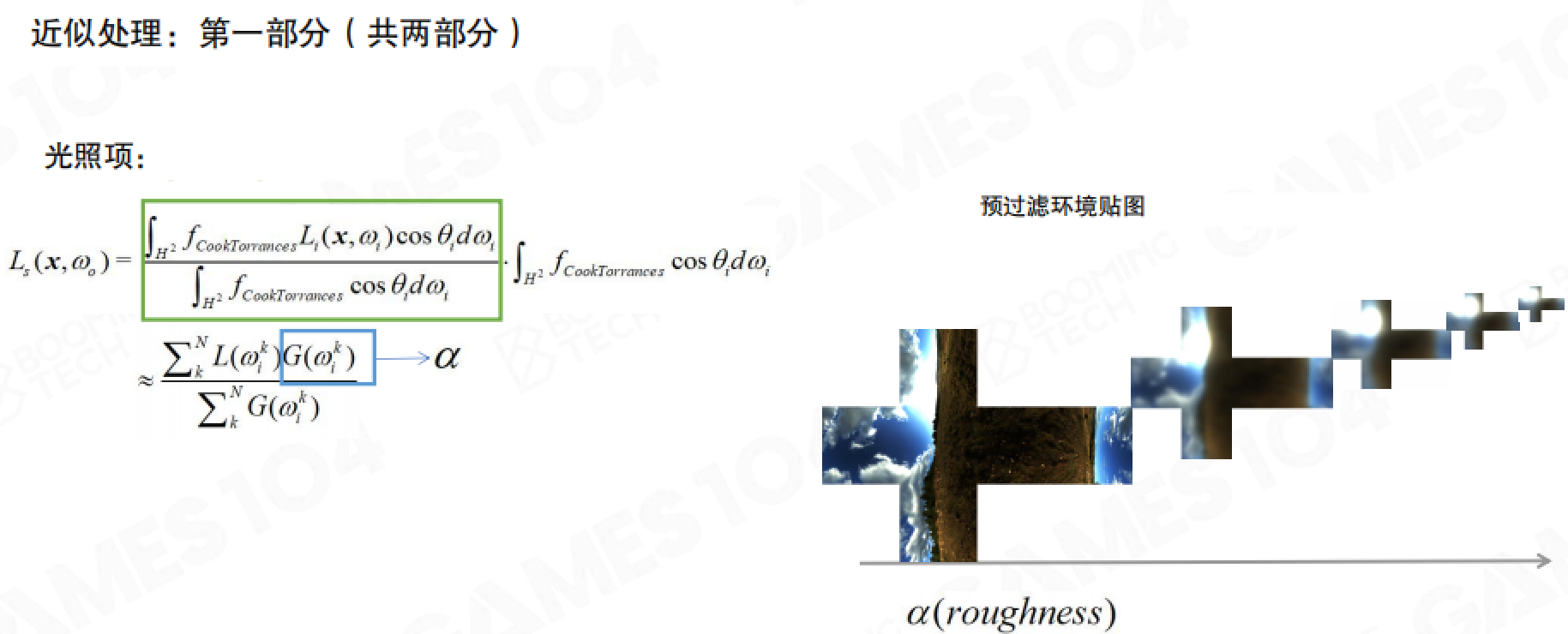
Mipmap层级
通常我们将不同粗糙度的预过滤环境贴图存储在Mipmap的不同层级中,粗糙度越大,使用越高的Mipmap层级(越模糊的贴图)。运行时,根据材质的粗糙度值选择对应的Mipmap层级进行采样。
这样,光照项的计算就变成了简单的纹理采样,非常高效。
BRDF项:查找表(LUT)
BRDF项描述了材质本身的反射特性,它依赖于粗糙度和观察角度(通过菲涅尔项)。我们可以将这个积分项预计算并存储在一张查找表(Look-Up Table, LUT)中。
Fresnel近似
利用Fresnel项的Schlick近似,我们可以将BRDF项进一步分解:
\[
\int_{H^2} f_{CookTorrance} \cos \theta_i d\omega_i \approx F_0 \cdot A + B
\]
其中 ( F_0 ) 是材质的Fresnel反射率,( A ) 和 ( B ) 是只依赖于粗糙度和观察角度的项。
LUT存储
我们将 ( A ) 和 ( B ) 分别存储在LUT的R和G通道中:
- LUT的X轴:( \cos \theta )(观察角度的余弦)
- LUT的Y轴:( \alpha )(粗糙度)

运行时,我们根据粗糙度和观察角度在LUT中查找对应的 ( A ) 和 ( B ) 值,然后计算 ( F_0 \cdot A + B ) 即可得到BRDF项。
基于预计算的快速着色
将上述所有预计算结果组合起来,我们就得到了完整的IBL着色公式:
\[
L(\omega_o) = k_d \cdot \text{IrradianceMap}(n) + \text{PreFiltered}(R, \alpha) \cdot (F_0 \cdot \text{LUT}.r + \text{LUT}.g)
\]
其中:
- 第一项(漫反射):根据法线方向采样辐照度图,乘以漫反射系数
- 第二项(高光):根据反射方向和粗糙度采样预过滤环境贴图,乘以BRDF项(从LUT中查找)

实现优势
这种预计算的方式将复杂的积分计算转换为简单的纹理采样和查表操作,计算量极小,完全满足实时渲染的要求。同时,由于使用了真实的环境图像,渲染结果非常真实自然。
IBL的视觉效果
IBL对渲染质量的提升是显著的。没有IBL时,阴影区域会完全漆黑,缺乏细节;有了IBL后,阴影区域会被环境光照柔和地照亮,展现出丰富的细节和真实的材质感。

在现代3A游戏中,IBL已经成为实现逼真渲染效果的标准技术。它让游戏画面能够真实地反映环境光照,大大提升了视觉质量。
5.7 经典阴影方法
阴影是渲染中增强场景真实感的重要元素。实时渲染中的阴影技术经历了从简单的硬阴影到复杂的软阴影的发展过程,级联阴影(Cascade Shadow Maps, CSM)是其中最重要的技术之一,它解决了大世界场景中阴影精度不足的问题。
Shadow Map基础
Shadow Map是实时渲染中最常用的阴影技术。其基本原理是:在光源处放置一台虚拟摄像机,从光源的视角渲染场景,生成一张深度图(Shadow Map),记录每个像素到光源的最近距离。
在渲染接收阴影的物体时,我们将像素点转换到光源空间中,与Shadow Map中记录的深度值进行比较。如果像素位置在Shadow Map记录的深度前方,说明该点被光源照亮;反之,则说明该点处于阴影中。
精度问题
Shadow Map最大的问题是精度不足。当视野范围较大时,所需的阴影精度可能较低;但当视野范围缩小时,就需要较高精度的阴影。然而,Shadow Map的采样区域和分辨率是相对固定的,无法同时满足近处和远处的精度需求。
此外,根据透视原理,距离人眼较近的位置阴影应该更清晰,远离人眼的阴影相对模糊。单一的Shadow Map无法很好地处理这种精度差异。
级联阴影(Cascade Shadow Maps)
为了解决Shadow Map的精度问题,级联阴影(Cascade Shadow Maps, CSM)应运而生。它的核心思想是:根据距离来调整阴影贴图的精度,近处使用高精度,远处使用低精度。
基本思想
CSM将视锥体由近到远分割成若干个子视锥体,每个子视锥体对应一张不同分辨率的阴影贴图。接近摄像机的区域使用高精度纹理采样,远离摄像机的区域使用低精度纹理采样。这种分级处理符合透视原理,既保证了近处阴影的清晰度,又减少了内存开销。

实现步骤
级联阴影的实现包括以下步骤:
- 分割视锥体:将主摄像机的视锥体分割为多个子视锥体
- 计算投影矩阵:为每个子视锥体从光源视角计算正交投影矩阵
- 渲染阴影贴图:为每个子视锥体渲染一张阴影贴图
- 渲染场景:在像素着色器中,根据像素位置选择最匹配的阴影贴图进行采样

在像素着色器中,我们需要:
- 将世界坐标转换到每个级联的投影空间中
- 采样所有相关的阴影贴图
- 比较深度值并计算光照
级联之间的混合
不同级联之间由于分辨率不匹配,在重叠区域会出现可见的接缝。为了解决这个问题,我们可以在级联边界处设置一个混合带,着色器根据像素在混合带中的位置,对相邻两个级联的阴影值进行线性插值,实现平滑过渡。

优缺点
级联阴影的优点:
- 有效解决阴影透视锯齿问题,是处理大世界阴影的最佳方法
- 计算快速,仅深度写入时速度可提升3倍
- 提供相当不错的阴影效果
级联阴影的缺点:
- 几乎无法生成高质量的区域阴影
- 阴影没有色彩,半透明表面只能投射不透明阴影
- 需要大量存储空间和计算时间

硬阴影与软阴影
传统的Shadow Map产生的是硬阴影(Hard Shadow),阴影边缘非常锐利,看起来不够自然。现实世界中的阴影通常是软阴影(Soft Shadow),边缘柔和,有半影(Penumbra)效果。

软阴影的产生是因为现实中的光源有大小,而不是一个点。光源的不同部分会被遮挡物不同程度地遮挡,形成从完全阴影到完全光照的渐变区域,这就是半影。
PCF - 百分比渐近滤波
PCF(Percentage Closer Filtering)是最早用于软化阴影边缘的技术。它的基本思想是:在当前像素周围对阴影贴图进行多次采样,将像素深度与所有采样点的深度进行比较,然后对比较结果进行平均处理。

实现原理
PCF通过增加采样点数量来平滑阴影边缘。采样点越多(如9x9、17x17),阴影边缘越柔和,但计算成本也越高。这种方法虽然能产生软阴影效果,但并不是基于物理的,只是视觉上的平滑处理。
PCF有效解决了阴影贴图产生的锯齿问题,在光线与阴影之间产生了更平滑的过渡,是实时渲染中常用的阴影平滑技术。
PCSS - 百分比渐近柔和阴影
PCSS(Percentage-Closer Soft Shadows)是一种基于物理的软阴影技术,它能够根据光源大小和遮挡关系计算真实的半影宽度。
基本思想
PCSS在阴影贴图中搜索并对靠近光源的深度值进行平均,然后使用平行平面近似法计算半影宽度。半影宽度的计算公式为:
\[
w_{Penumbra} = \frac{(d_{Receiver} - d_{Blocker}) \cdot w_{Light}}{d_{Blocker}}
\]
其中:
- ( w_{Light} ) 是光源的宽度
- ( d_{Blocker} ) 是遮挡物到光源的距离
- ( d_{Receiver} ) 是接收面到光源的距离

实现过程
PCSS的实现分为三个步骤:
- 搜索遮挡物:在阴影贴图中搜索遮挡当前像素的深度值
- 计算半影宽度:根据遮挡物距离和光源大小计算半影宽度
- 自适应PCF:根据半影宽度调整PCF的采样范围
PCSS能够产生更加自然和真实的软阴影效果,但计算成本较高,因为需要对阴影贴图进行多次搜索和采样。
方差软阴影贴图(VSSM)
VSSM(Variance Soft Shadow Mapping)是一种高效的软阴影近似方法,它基于切比雪夫不等式(Chebyshev’s Inequality)来估计像素上的阴影比例,避免了PCSS中大量的搜索和采样操作。
基本理念
VSSM利用深度的平均值和方差,可以直接近似深度分布的百分比,而无需将单个深度与特定区域进行比较。这种方法不需要假设深度分布是高斯分布,适用范围更广。
数学基础
切比雪夫不等式告诉我们,对于随机变量 ( x ),其均值 ( \mu = E(x) ),方差 ( \sigma^2 = E(x^2) - E(x)^2 ),有:
\[
P(x > t) \leq \frac{\sigma^2}{\sigma^2 + (t - \mu)^2}
\]
这个不等式给出了 ( x > t ) 的概率上界,我们可以用它来估计阴影的遮挡程度。

实现优势
VSSM只需要存储深度的均值和方差(可以使用Mipmap或特殊的纹理格式),运行时只需要一次纹理采样和简单的数学计算,就能得到软阴影效果。这使得VSSM的计算效率远高于PCSS,能够实现实时的高质量软阴影。
不过,VSSM在某些情况下可能会出现块状伪影,而PCSS虽然计算成本高,但质量更好。在实际应用中,需要根据性能和质量需求进行权衡。
现代3A游戏的渲染技术
将上述所有技术结合起来——光照贴图、光照探针、基于物理的渲染、图像化光照、级联阴影、软阴影技术等——就可以实现现代3A游戏的渲染效果。

这些技术的组合使用,让游戏画面能够真实地反映光照、材质和阴影,创造出令人惊叹的视觉效果。级联阴影解决了大世界场景的阴影精度问题,PCF和PCSS提供了自然的软阴影效果,VSSM则在性能和质量之间找到了平衡点。
在现代游戏引擎中,这些阴影技术已经成为标准配置,它们共同构成了实时渲染中阴影系统的完整解决方案。
5.8 前沿技术
随着GPU硬件性能的飞速提升和新型着色器模型的提出,实时渲染技术正在经历一场革命。传统的预计算和近似方法已经无法完全满足人们对画质的需求,实时光线追踪、实时全局光照等前沿技术正在将实时渲染推向新的高度。
GPU的飞速演进
现代GPU的演进为实时渲染技术的突破提供了硬件基础。这种演进主要体现在三个方面:
更灵活的新型着色器模型
传统的顶点着色器和像素着色器已经无法满足复杂渲染需求,新的着色器模型应运而生:
- 计算着色器(Compute Shader):允许GPU进行通用计算,不再局限于图形渲染,为各种后处理效果和计算任务提供了强大的并行计算能力
- 网格着色器(Mesh Shader):提供了更灵活的几何处理流程,能够动态生成和剔除几何体,实现几乎无限的几何细节
- 光线追踪着色器(Ray Tracing Shader):专门为光线追踪设计的着色器,包括Ray Generation、Intersection、Any-Hit、Closest-Hit和Miss着色器
高性能并行架构
现代GPU采用Warp(NVIDIA)或Wave(AMD)架构,将多个线程组织成执行单元,实现高效的并行计算。这种架构特别适合图形渲染和光线追踪等高度并行的任务。
完全开放的图形API
DirectX 12和Vulkan等新一代图形API提供了更底层的硬件控制能力,让开发者能够更精细地管理GPU资源,充分发挥硬件性能。

这些硬件和API的进步,为实时光线追踪、实时全局光照等前沿技术的实现奠定了基础。
实时光线追踪(Real-Time Ray Tracing)
前面介绍的全局光照算法,如LightMap、LightProbe等,虽然能够产生不错的效果,但它们都依赖于预计算或各种近似假设,并非真正的实时光照处理。随着新一代GPU硬件的支持,实时光线追踪技术正在突破实时渲染的边界。
硬件加速
2018年,NVIDIA发布了Turing架构,这是首个支持硬件加速光线追踪的GPU架构。Turing架构中的RT Core专门用于加速光线与包围盒和三角形的相交测试,大大提高了光线追踪的计算效率。同年,搭载实时光线追踪技术的RTX系列显卡正式发布,第一款支持RTX实时混合光线追踪技术的游戏《战地5(Battlefield V)》也正式面世。
光线追踪流程
在GPU上实现实时光线追踪的流程包括:
- 光线生成(Ray Generation):从摄像机或光源生成初始光线
- 加速结构遍历(Acceleration Traversal):使用BVH等加速结构快速找到可能相交的几何体
- 相交测试(Intersection):计算光线与几何体的精确交点
- 任意命中着色器(Any-Hit Shader):处理透明或半透明物体的命中
- 最近命中着色器(Closest-Hit Shader):计算最近交点的着色
- 未命中着色器(Miss Shader):处理未命中任何物体的光线(如天空、环境光)
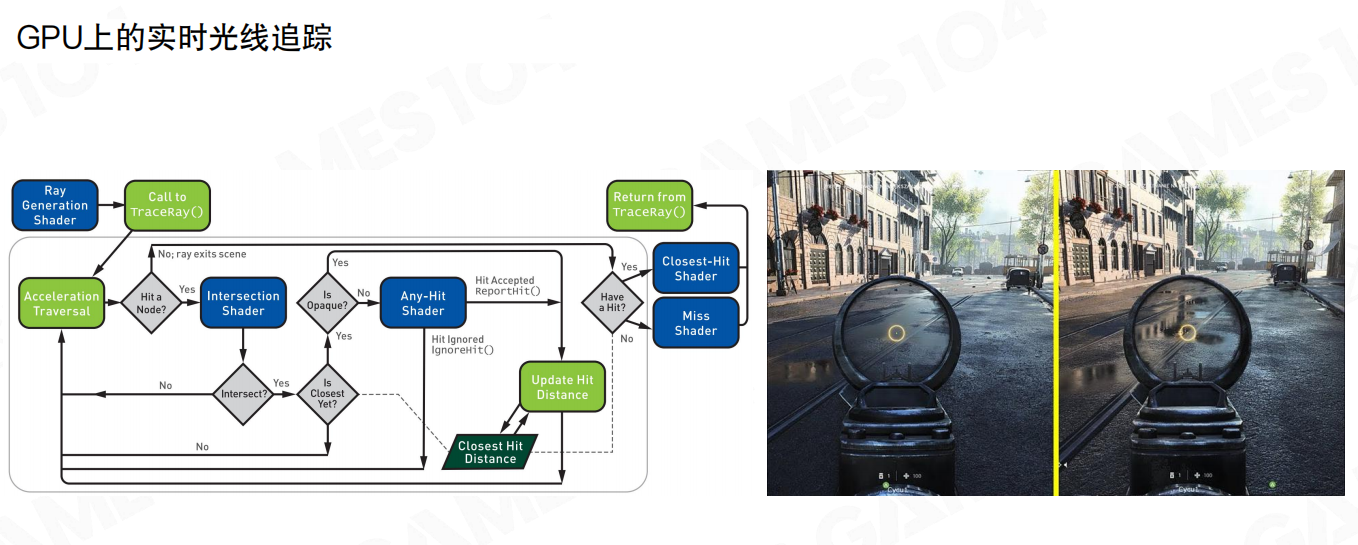
视觉效果
实时光线追踪能够产生极其真实的反射、折射和全局光照效果。在游戏中,我们可以看到水面、玻璃、金属等材质产生精确的环境反射,阴影也更加自然和准确。虽然实时光线追踪的计算成本仍然较高,但随着硬件性能的提升和算法的优化,它正在逐步走向大规模应用。
实时全局光照(Real-Time Global Illumination)
实时全局光照是另一个重要的前沿技术方向。虽然传统的预计算全局光照(如LightMap)能够产生很好的效果,但它们无法处理动态场景。实时全局光照技术能够在运行时计算间接光照,让动态场景也能拥有真实的光照效果。
主要技术
目前主流的实时全局光照技术包括:
- Screen-space GI:基于屏幕空间信息的全局光照,计算快速但受限于屏幕可见区域
- SDF Based GI:基于有向距离场(Signed Distance Field)的全局光照,能够处理遮挡关系
- Voxel-Based GI(SVOGI/VXGI):基于体素的全局光照,将场景体素化后计算间接光照
- RSM / RTX GI:基于反射阴影贴图(Reflective Shadow Maps)或光线追踪的全局光照
体素化GI原理
体素化GI技术将场景划分为体素网格,然后从光源发射光线,计算光线在体素中的传播和反弹。对于每个着色点,使用漫反射锥(Diffuse Cone)和高光锥(Specular Cone)来采样间接光照,实现真实的全局光照效果。

性能与质量
实时全局光照能够显著提升画面的真实感,特别是在阴影区域和间接光照区域。从性能数据来看,现代实时GI技术已经能够在保持较高帧率的同时提供出色的视觉效果。例如,在《战争机器》等游戏中,开启实时全局光照后,画面质量大幅提升,而性能开销相对可控。
更复杂的材质模型
随着渲染技术的发展,人们对材质真实感的要求越来越高。传统的BRDF模型已经无法满足头发、皮肤等复杂材质的渲染需求,更复杂的材质模型应运而生。
头发渲染:BSDF
头发渲染需要使用双向散射分布函数(BSDF, Bidirectional Scattering Distribution Function)。头发由大量细小的发丝组成,光线在发丝内部会发生多次散射和反射,形成复杂的光照效果。BSDF模型能够准确描述光线在发丝中的传播,实现高度真实的头发渲染。
皮肤渲染:BSSRDF
皮肤等半透明材质需要使用双向散射表面反射分布函数(BSSRDF, Bidirectional Scattering Surface Reflection Distribution Function)。BSSRDF是BSDF的扩展,它不仅考虑光线在表面的反射,还考虑光线进入材质内部后的散射和从其他点射出的情况。这种模型能够准确模拟皮肤、蜡、大理石等半透明材质的次表面散射效果。

应用前景
这些复杂的材质模型结合几何着色器等新技术,使得实时渲染能够表现出几乎无限的几何细节和材质细节。在电影级画质的游戏中,我们可以看到人物角色的头发、皮肤等细节都达到了前所未有的真实程度。
虚拟阴影贴图(Virtual Shadow Maps)
传统的级联阴影虽然能够处理大世界场景,但仍然存在存储空间浪费的问题。虚拟阴影贴图(Virtual Shadow Maps, VSM)技术借鉴了虚拟纹理(Virtual Texture)的思想,能够更高效地利用存储空间。
基本原理
虚拟阴影贴图首先计算场景中哪些区域需要阴影贴图,然后在虚拟的阴影贴图空间中为这些区域分配空间。每个小块生成独立的阴影贴图,这些阴影贴图被打包(Packed)到一个物理纹理中。在计算阴影时,通过反向查找来获取对应小块的数据。
优势
这种处理方式相比传统的级联阴影有以下优势:
- 更高效的存储利用:只为实际需要的区域分配阴影贴图,避免浪费
- 更高的精度:可以根据需要为不同区域分配不同精度的阴影贴图
- 更好的灵活性:可以动态调整阴影贴图的分配,适应动态场景

实际应用
虚拟阴影贴图技术已经在虚幻5引擎中得到应用,为游戏提供了更加逼真和高效的阴影效果。这种技术特别适合大世界开放游戏,能够在保持高性能的同时提供高质量的阴影。
5.9 Shader管理
在现代3A游戏中,每一帧的画面上可能都有上千个shader在运行。如何高效地组织、编译和管理这些shader,就是Shader管理的核心问题。
Shader的规模
现代游戏中的shader数量庞大。以《命运(Destiny)》为例,游戏中的各种环境场景都需要大量的shader来渲染。
不同场景的shader复杂度差异巨大:一个封闭的室内场景每帧可能需要约3500个shader技术,而一个开放的大世界场景可能需要约9000个shader技术。

艺术家创造的多样性
现代游戏引擎提供了强大的可视化shader编辑工具。艺术家可以通过节点编辑器创建各种独特的shader图和材质,而无需直接编写shader代码。在一个真实的游戏项目中,艺术家可能创作了17,800+个独特的shader图和材质。

Uber Shader:一个”超级”shader解决所有问题
面对如此庞大的shader数量,如果为每种可能的组合都单独编写shader,工作量将是不可想象的。现代游戏引擎采用了Uber Shader(超级着色器)的概念:一个组合了所有可能的光照类型、渲染通道和材质类型的综合shader,通过预定义的宏在编译时生成大量独立的shader变体。

Uber Shader使用预处理器指令(#if、#endif等)来条件性地包含或排除代码。在编译时,编译器会根据定义的宏生成不同的shader变体,每个变体只包含需要的代码,避免了运行时的条件判断开销。
Uber Shader的优势:代码共享、编译时生成优化过的变体、易于维护。
Shader变体的实际规模
在实际游戏中,Uber Shader系统会产生大量的shader变体。例如,在一个真实的游戏项目中,165个超级着色器在运行时生成了75,536个独立的shader。
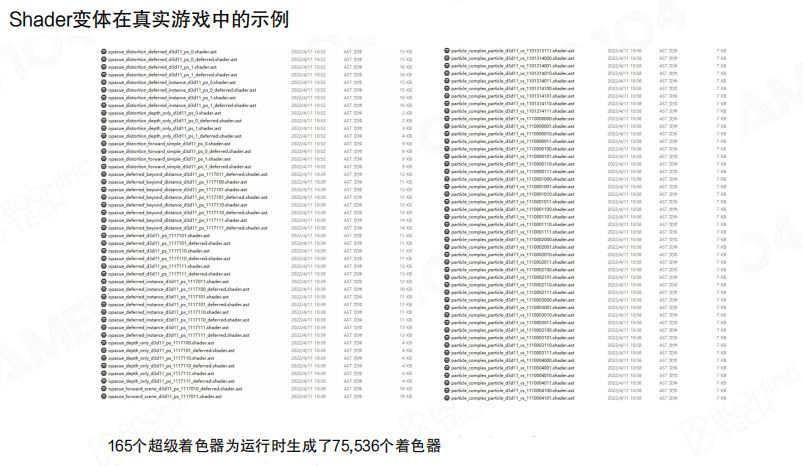
每个变体都是针对特定情况优化的,这种”按需生成”的方式既保证了性能,又避免了代码冗余。
跨平台编译
不同的游戏平台使用了不同的图形API(DirectX、Vulkan、Metal、OpenGL等)。现代游戏引擎通常采用统一的shader源语言(如HLSL),然后通过编译工具链将其编译为不同平台的shader代码。
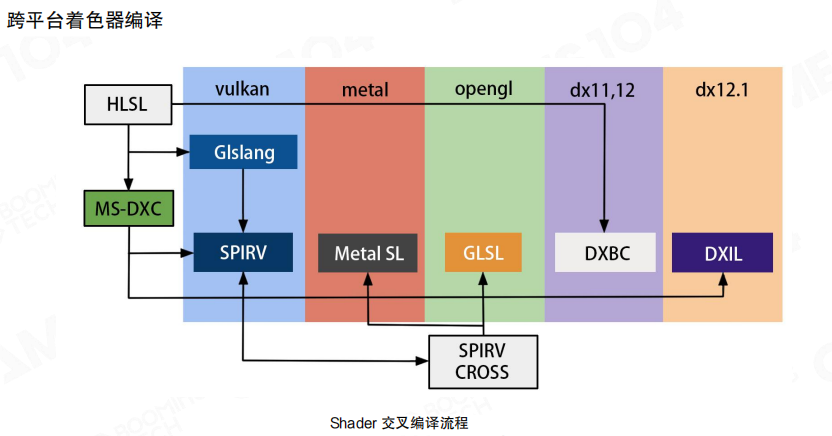
编译流程包括:直接编译(HLSL → SPIRV/DXBC/DXIL)和交叉编译(通过SPIRV CROSS将SPIRV转换为Metal SL、GLSL等)。
转载请注明来源,欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。可以在下面评论区评论,也可以邮件至 785293209@qq.com

