8.游戏引擎的动画技术基础

游戏引擎 > 引擎体系 > 现代游戏引擎入门游戏引擎引擎体系现代游戏引擎入门

发布时间 : 2025-11-19 12:38

字数:13.4k 阅读 :

评论:

8.游戏引擎的动画技术基础

8.游戏引擎的动画技术基础

8.1 动画技术简介

动画系统是游戏引擎的重要组成部分。利用人眼的「视觉残留」效应（影像残留约1/24秒）和「视错觉运动」现象，通过快速切换静态画面模拟连续运动，这是所有显示设备和动画的理论基础。

动画技术发展历程

游戏行业的动画基础理论和工具都来自于电影行业。从早期的手绘动画、赛璐珞动画，到计算机动画（《侏罗纪公园》1993、《阿凡达》2009），再到实时渲染动画（《扎法里》2018），动画技术不断演进。动作捕捉技术通过多摄像机追踪标记点恢复人物动作，广泛应用于现代制作。

游戏动画技术演进

2D精灵动画：从《吃豆人》（1980）的简单帧切换，到《波斯王子》（1989）的逐帧转描技术（Rotoscoping），再到《毁灭战士》（1993）的多视角精灵动画，通过2D技术营造3D空间感。

3D动画技术：从《生化危机》（1996）的刚性层级动画，到《半衰期》（1998）的软蒙皮动画，再到《神秘海域4》（2016）的物理动画，实现了从简单骨骼运动到真实环境交互的跨越。

游戏动画的核心挑战

与电影动画不同，游戏动画面临三大挑战：

交互式动态动画：无法预设玩家行为，需要根据用户输入和环境变化灵活调整，与其他游戏系统协同运作
实时性能挑战：所有计算必须在30ms内完成，动画数据量大，需要压缩等技术优化
真实感要求：需要动作匹配、物理动画、面部动画等技术实现高保真度表现

动画系统技术体系

现代游戏引擎的动画系统分为基础技术（2D/3D动画、蒙皮动画、动画压缩、DCC）和高级技术（动画混合、IK、动画管线、动画图表、面部动画、重定向）两部分。

8.2 2D游戏动画技术

2D动画是最早的游戏动画形式，直到今天仍然有很多游戏在使用。2D动画技术主要有两种：精灵动画和Live2D。

精灵动画（Sprite Animation）

精灵其实就是一种小型位图，可以叠加在背景图像上而不会破坏背景。我们把游戏角色的动作逐帧绘制成精灵序列，然后在游戏里循环播放，利用视觉暂留效应就能产生动画效果。这其实就是电子版的赛璐珞动画。

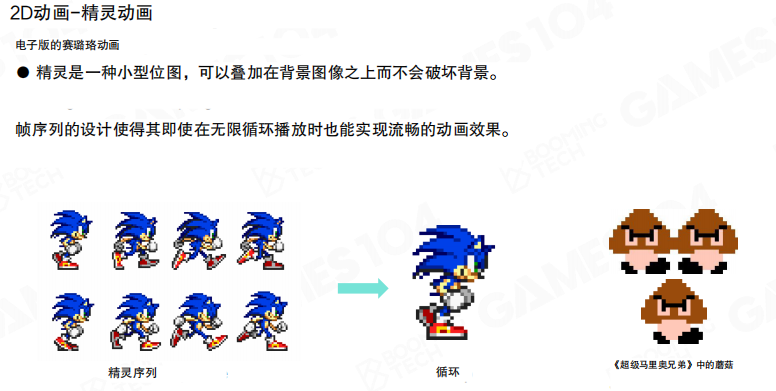
实现起来很简单：把动画的每一帧都画成独立的精灵图片，按时间间隔顺序播放就行。帧序列设计得好，即使无限循环播放也能很流畅。为了优化性能，通常会把多帧动画打包到一张大图里，通过UV坐标偏移来实现帧切换。

如果想要更生动的效果，可以在不同视角下绘制同一动作，游戏里根据角色方向选择合适的动作帧播放。这样就能用2D动画做出伪3D的效果。比如《毁灭战士》（1993）就用了这种技术，通过8个视角的精灵动画，让玩家感觉在真正的3D空间里移动。

现在精灵动画依然很有用。很多游戏的特效都是通过预先渲染的特效帧来实现的，比如爆炸、火焰、魔法效果这些。而且2D角色还能和3D环境结合，像《八方旅人》那样，2D像素风格的角色配上3D渲染的环境，视觉效果很独特。

Live2D技术

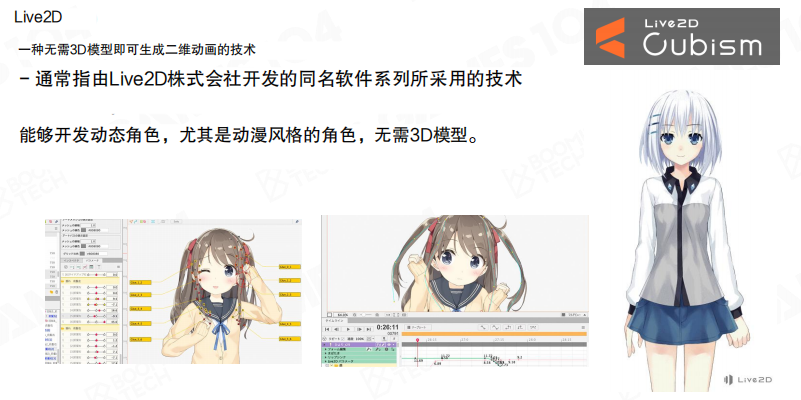
Live2D是一种不需要3D模型就能生成2D动画的技术，通过对图像进行变形就能实现很生动的效果。现在虚拟主播里用的Live2D技术就是这种，特别适合做动漫风格的角色。

Live2D的做法是把角色的各个部位拆分成不同的元素，然后对每个元素进行变形来实现不同的动作。具体来说，就是对图元局部做Transform和spine变换，模拟局部动画效果。

制作流程大致分三步：

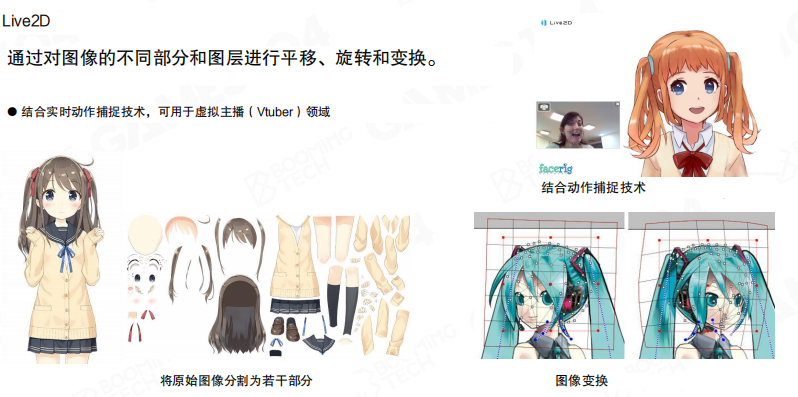
资源准备：先把原始角色图像分割成不同部件，给每个部件设置好”绘制顺序”。放置不同元素时，通过调整图层顺序还能进一步提升表现力。

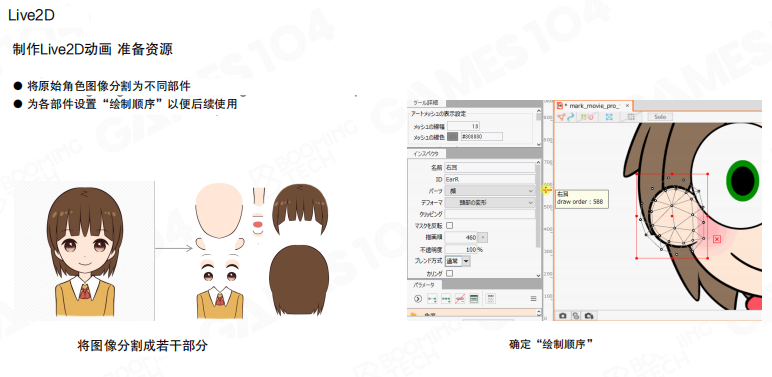
网格设置：每个图元都需要设置好网格（ArtMesh）来控制形变。ArtMesh可以自动生成，由顶点、边和多边形定义。通过控制点可以辅助变换ArtMesh，角色的不同动作就是通过对网格控制点的运动来描述的。

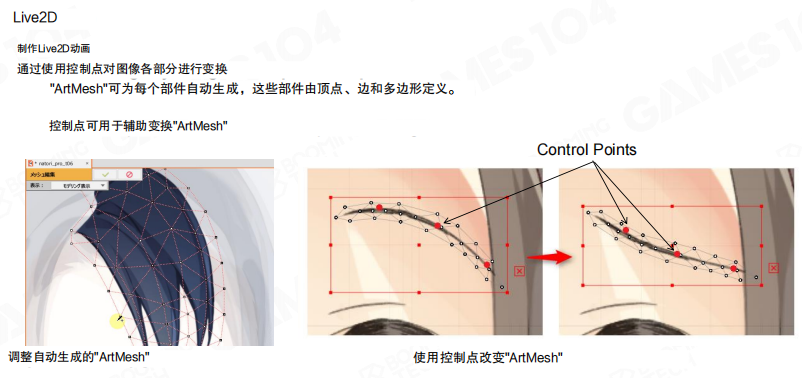
关键帧动画：设置好动画的关键帧，系统会自动插值。最后把角色不同元素、不同控制点的运动组织起来，一个虚拟角色的动作就完成了。

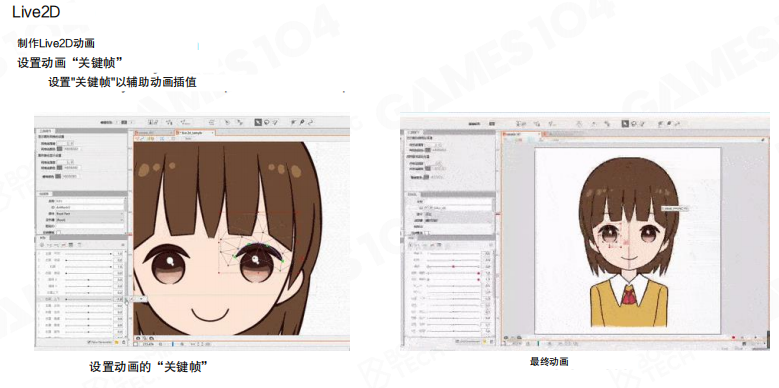
Live2D通过平移、旋转和变换图像的不同部分和图层，再结合实时动作捕捉技术，现在主要用在虚拟主播（Vtuber）领域，能实现实时的面部表情和动作捕捉。

8.3 3D游戏动画技术

3D动画技术比2D复杂一些，在介绍具体技术前，我们先看看相关的数学基础。

自由度（Degrees of Freedom）

自由度指的是系统中独立变量或参数的数量。对于三维空间中的刚体来说，描述它的运动需要6个自由度：3个平移自由度（沿X、Y、Z轴的移动）和3个旋转自由度（绕X、Y、Z轴的旋转，也就是Roll、Yaw、Pitch）。

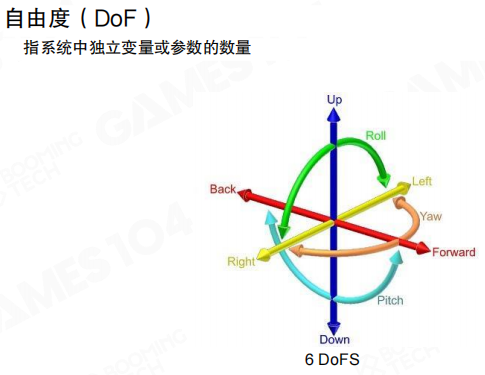
比如门的平移、风车的旋转、轮胎的平移与旋转，这些都是刚体运动的典型例子。理解自由度概念对后续理解各种动画技术很重要。

刚性层级动画（Rigid Hierarchical Animation）

这是最简单的3D动画技术。把角色的不同部位都当成刚体，然后按照一定的层次组织起来。角色被建模为一系列刚性部件的集合，这些部件以层级方式相互约束，就像传统的皮影戏一样。

早期的3D游戏就是用这种方法，比如《生化危机》（1996）。但这种方法有个问题：只移动硬骨骼，部件之间没有平滑过渡，关节处容易出现”断裂”的感觉，看起来不够自然。

顶点动画（Per-vertex Animation）

另一种方法是直接控制网格的顶点。每个顶点有3个平移自由度，通过对顶点坐标的变换就能实现模型运动。在顶点着色器中可以对顶点随时间进行处理，可以用数学函数，也可以用预先计算好的纹理数据。

顶点动画最灵活，但需要海量数据。主要通过顶点动画纹理（VAT）实现，把每个顶点的位移和旋转信息编码到纹理里。这种方法在人物角色上用得不多，但在物理仿真中很常见，比如布料动画、流体动画这些复杂形变效果。

形变目标动画（Morph Target Animation）

这是顶点动画的一种变体，也叫Shape Key Animation。和顶点动画不同的是，它不直接操作顶点坐标，而是通过顶点的位置和权重来控制整个网格的行为。使用关键帧配合线性插值（LERP）来替代序列帧，比如每秒30帧。

形变目标动画特别适合做面部表情。先定义几个关键姿态（比如中性、微笑、皱眉），然后通过线性插值在这些姿态之间过渡，就能做出流畅的表情变化。

骨骼动画（Skinned Animation）

蒙皮动画是目前游戏行业最主流的3D动画技术。网格（或蒙皮）绑定在骨骼的关节上，通过控制角色内部骨骼的运动来实现整个角色的运动。每个顶点可以被赋予多个关节的权重，这样网格就能以自然的方式实现动画效果，就像人类的皮肤一样。

和刚体动画相比，蒙皮动画在关节处连续且流畅，能实现更真实自然的运动效果。蒙皮动画同样可以应用在2D动画上，把角色拆分成多个身体部位，创建网格并拼接，然后进行骨骼绑定、蒙皮和动画制作。

基于2D蒙皮动画的运动比刚体动画有更自然的表现效果。

基于物理的动画（Physics-based Animation）

除了蒙皮动画，还有一大类动画形式是基于物理的动画。这是完全基于物理法则的动画模拟方法，需要更深入的数学物理知识。主要包括：

布娃娃系统（Ragdoll）：角色受击或死亡时的物理模拟，比如GTA5中的布娃娃系统
布料与流体模拟：衣料、头发等物体的物理运动，比如UE5《远古之谷》中的布料效果
反向动力学（IK）：根据末端位置计算关节角度，比如《神秘海域4》中的攀爬动画

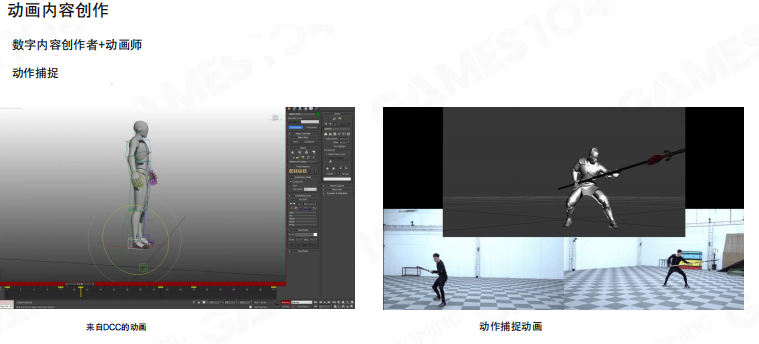
动画内容创作

那么动画是怎么制作出来的呢？主要有两种方式：

一种是传统的数字内容创作（DCC），动画师在专业软件中通过关键帧来对角色的动作进行建模，然后通过插值处理生成完整动画。

另一种是动作捕捉（Motion Capture），通过真人表演来获得更自然的运动动画。现在越来越多的游戏和电影都在用动捕技术，能捕捉到非常真实的人体运动细节。

8.4 蒙皮动画的实现

蒙皮动画的实现看起来简单，实际上并不容易。下面我们来看看具体的实现细节。

如何为网格添加动画

蒙皮动画的实现包括5个步骤：

为绑定姿势创建网格：先创建一个基础姿态的网格模型
为网格创建绑定骨架：建立网格模型附着的骨骼，确定骨骼影响哪些顶点
将蒙皮权重”绘制”到关联骨骼的每个顶点上：为网格上每个顶点赋予骨骼对应的权重
将骨骼动画调整至目标姿态：利用骨骼完成角色的运动
通过骨骼和蒙皮权重对蒙皮顶点进行动画处理：结合顶点的骨骼权重实现网格的运动

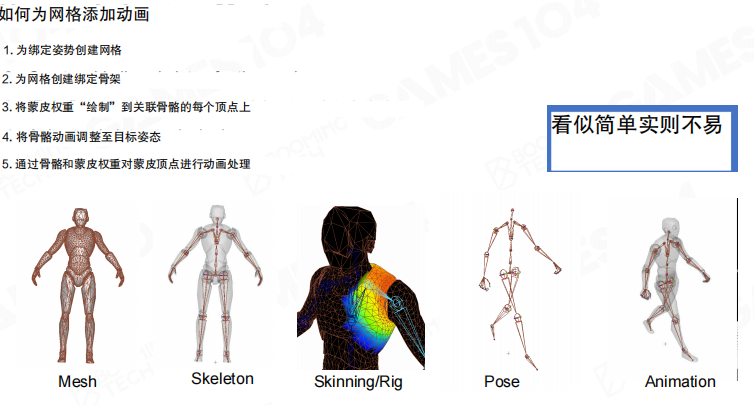
这5个步骤看起来不难，但在实际编程中需要多加小心，防止出现网格爆炸的问题。

坐标系系统

要描述骨骼的运动，我们需要引入相应的坐标系统。主要有三种：

世界空间（World Space）：包含所有物体的坐标系，整个游戏世界都定义在这个坐标系中
模型空间（Model Space）：模型制作时的坐标系，每个单独的模型都有自己的模型坐标系
局部空间（Local Space）：当有其它物体相对于自身表示时的坐标系，骨骼的计算也是在这一坐标系中进行的

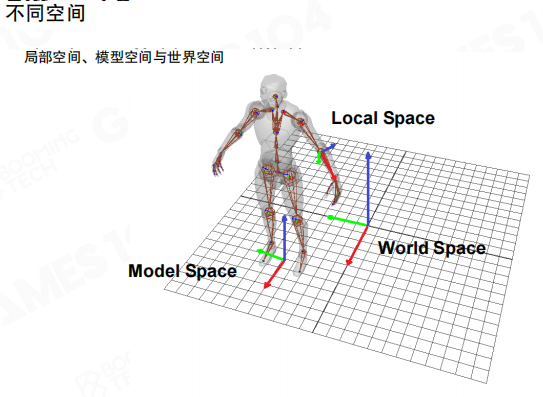
任意两个坐标系之间的变换关系可以通过3个平移和3个旋转一共6个自由度来表示。这样每个顶点的坐标都可以从局部坐标系变换到模型坐标系，再变换到世界坐标系上。

生物骨骼

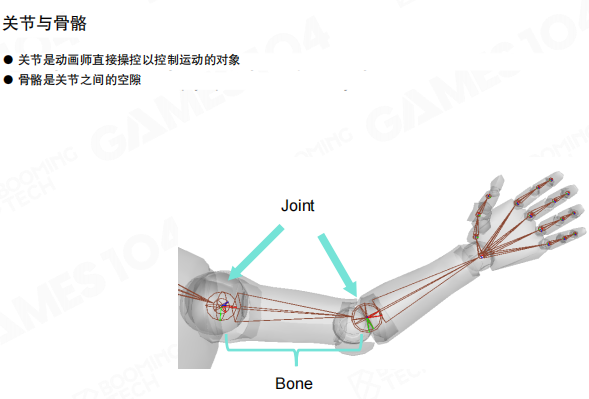
动画师在设计骨骼时，通常会有一套标准的骨骼，在此基础上进行角色动画的制作。这些骨骼由一系列的刚性关节（joint）组成，两个关节之间就是一根骨骼（bone）。

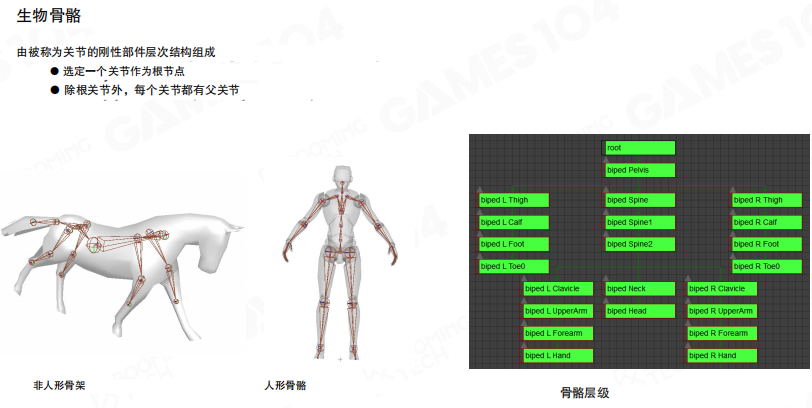
关节是动画师直接操控以控制运动的对象，骨骼是关节之间的空隙。实际上我们不会直接按照骨骼进行编程，而是利用关节及它们之间的连接关系来表达整个骨骼的运动。

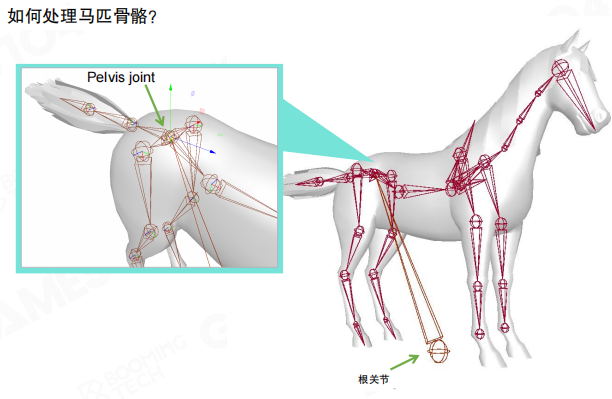
骨骼模型一般可以通过一棵树来表示。选定一个关节作为根节点，除根关节外，每个关节都有父关节。对于类人型的骨骼，整棵树的根节点一般位于胯部（pelvis）。而对于四足动物等其它类型的骨骼，其根部则会位于其它位置，比如马的根关节在脚部中心，便于触地。

实际游戏中的骨骼复杂度

实际游戏中的类人骨架，关节数量差异很大。正常状态下通常有50~100个关节，但可能包含超过300个关节，包括面部关节和游戏玩法关节。

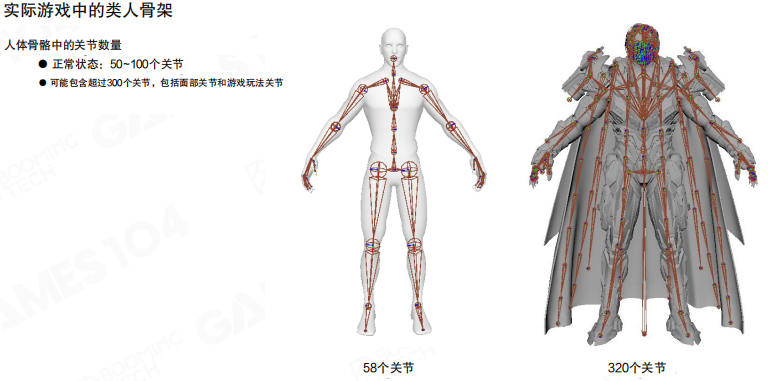
简单的角色可能只有58个关节，主要用于基础动画。而复杂的角色可能有320个关节，包括详细的面部表情关节、手指关节，以及用于斗篷、武器等附加元素的关节。

游戏玩法中的关节系统

在游戏建模中，除了常见的四肢外，还会根据角色的服装和特点来构建更复杂的骨骼模型。比如玩家手中的武器就是通过在角色手上绑定一个新的骨骼来实现的。

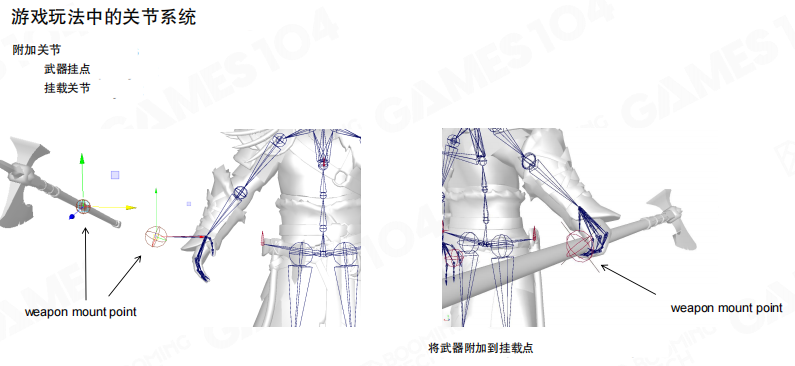
这种附加关节（attachment joint）也叫武器挂点（weapon mount point）或挂载关节（mount joint）。武器和角色手上都有对应的挂载点，通过将两个挂载点的坐标和朝向对齐，就能把武器正确地附加到角色手上。

根关节和骨盆关节

在进行建模时，我们往往还会定义一个root关节。不同于前面介绍过的胯部骨骼，root关节一般会定义在角色的两脚之间，这样方便把角色固定在地面上。根关节的第一个子关节是骨盆关节（pelvis joint），它便于实现人体上下半身的分离。

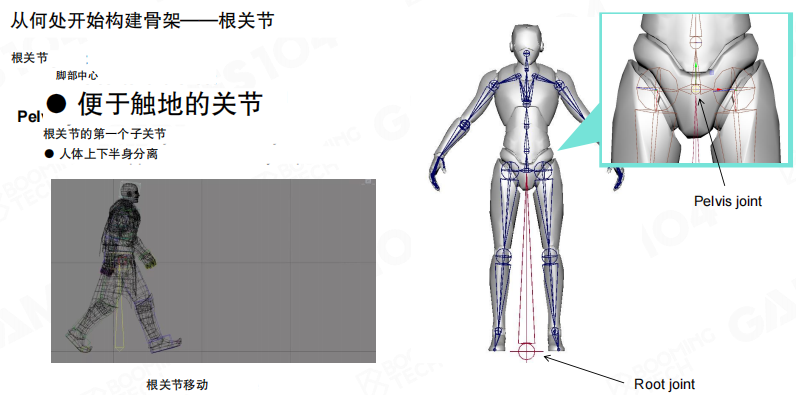
对于坐骑的骨骼，也往往会单独把root关节定义在接近地面的位置。比如马的骨骼，根关节在脚部，骨盆关节在臀部，这样能更好地处理四足动物的运动。

对象的绑定动画

很多游戏动画需要将不同的骨骼绑定到一起。最直观的例子就是角色骑马的动画，此时角色和马都有自身独立的动画，我们需要将它们组合到一起完成角色骑马的动作。

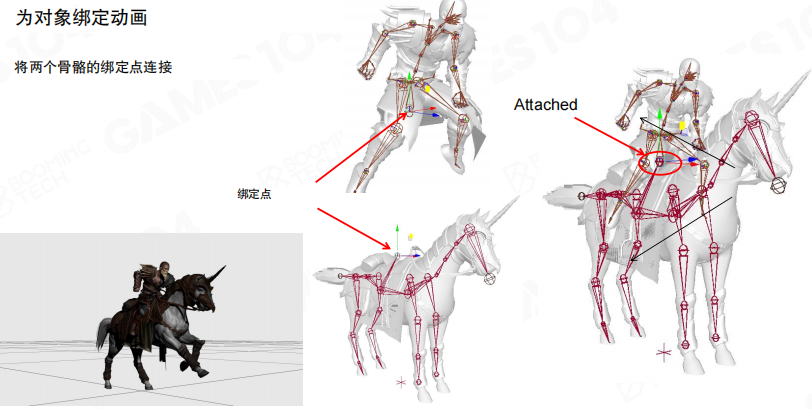
要实现这种功能，需要设计一个单独的mount关节，然后通过这个关节将两个模型拼接到一起。需要注意的是，在拼接时不仅要考虑关节坐标的一致性，更要保证两个模型的mount关节上有一致的朝向，这样才能实现模型正确的结合。

绑定姿势（Bind Pose）

绑定姿势是绑定骨骼前的三维网格姿态。通常保持四肢远离躯干且彼此分离，使顶点与关节的绑定过程更为便捷，通常接近自然姿态。

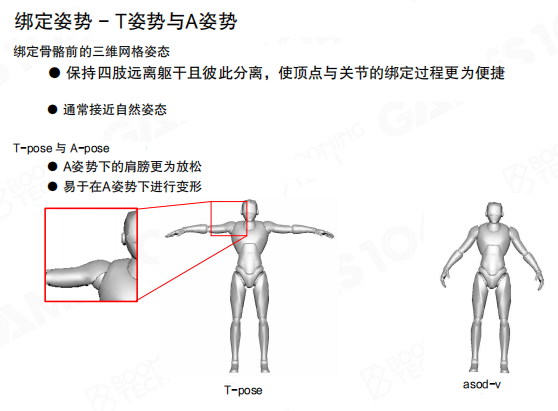
早期会使用T-pose作为角色动作的基准，但在实践过程中发现T-pose会导致角色的肩部出现挤压的状况，造成对这部分的骨骼权重精度不足。因此现代3A游戏中更多地会使用A-pose这种姿势进行建模。A姿势下的肩膀更为放松，易于在A姿势下进行变形。

骨骼姿态（Skeleton Pose）

完成骨骼建模后，角色的运动就可以通过骨骼的姿态来进行描述。骨骼姿态是通过变换关节从绑定姿态来调整骨骼的姿态。

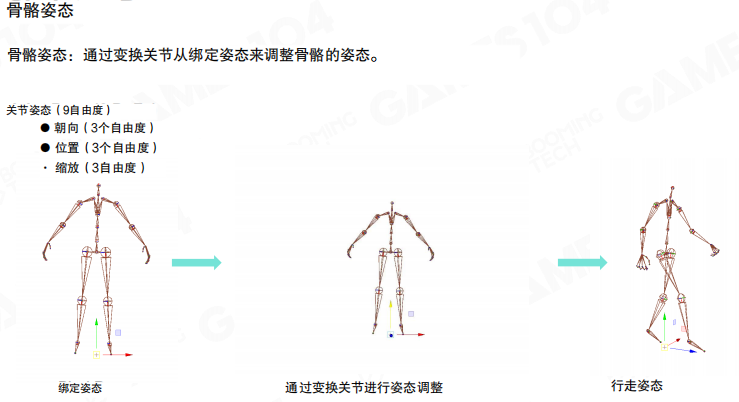
这里需要注意的是，表达角色的不同动作时，每个关节实际上具有9个自由度：朝向（3个自由度）、位置（3个自由度）和缩放（3个自由度）。除了刚体变换的6个自由度外，还需要考虑3个缩放变换引入的自由度。这3个缩放自由度对于表现一些大变形的动作起着很重要的作用。

8.5 3D旋转的数学原理

在游戏引擎中，物体的旋转是一个核心问题。如何表示和计算三维空间中的旋转，直接影响着动画系统、物理模拟和渲染管线的实现。本节将详细介绍3D旋转的数学原理，从2D旋转的回顾开始，逐步深入到欧拉角和四元数。

2D旋转回顾

在深入3D旋转之前，我们先回顾一下2D旋转的数学表示。对于二维空间中的点，当它绕原点进行旋转时，只需要一个旋转角度就可以进行描述。

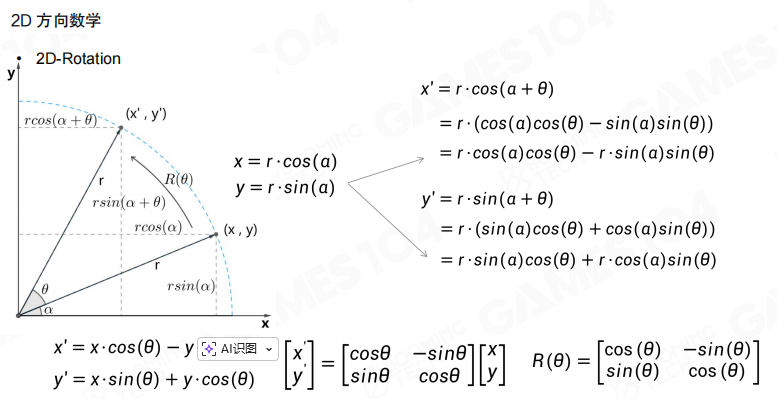
2D旋转矩阵：

对于点(x, y)绕原点旋转角度θ，旋转后的坐标为：
- x' = x * cos(θ) - y * sin(θ)
- y' = x * sin(θ) + y * cos(θ)
用矩阵表示为：[x'; y'] = [[cos(θ), -sin(θ)]; [sin(θ), cos(θ)]] * [x; y]

二维旋转只需要一个角度参数，表示简单直观。但在三维空间中，旋转变得更加复杂。

欧拉角（Euler Angle）

三维空间中的旋转要更复杂一些。我们可以把任意三维空间的旋转分解为绕三个轴的旋转，每个旋转都对应一个三维旋转矩阵，这样就可以通过绕三个轴的旋转角度来进行表达。这种描述三维旋转的方法称为欧拉角（Euler Angle）。

3D旋转矩阵：

绕X轴旋转：Rx(α) = [[1, 0, 0]; [0, cos(α), -sin(α)]; [0, sin(α), cos(α)]]
绕Y轴旋转：Ry(β) = [[cos(β), 0, sin(β)]; [0, 1, 0]; [-sin(β), 0, cos(β)]]
绕Z轴旋转：Rz(γ) = [[cos(γ), -sin(γ), 0]; [sin(γ), cos(γ), 0]; [0, 0, 1]]
组合旋转：R = Rx(α) * Ry(β) * Rz(γ)

欧拉角在很多领域都有大量的应用，比如说飞行器的导航和姿态描述一般都是基于欧拉角的。在飞行器中，通常使用偏航角（Yaw）、俯仰角（Pitch）和滚转角（Roll）来描述飞机的姿态。

欧拉角的问题

虽然欧拉角直观易懂，但它存在很多局限性，这些局限性使得游戏引擎中几乎不会直接使用欧拉角来表达物体的旋转。

旋转顺序依赖

欧拉角是依赖于旋转顺序的。在使用欧拉角时必须指明绕三个旋转轴进行旋转的顺序，同样的欧拉角按照不同的顺序进行旋转会得到不同的结果。

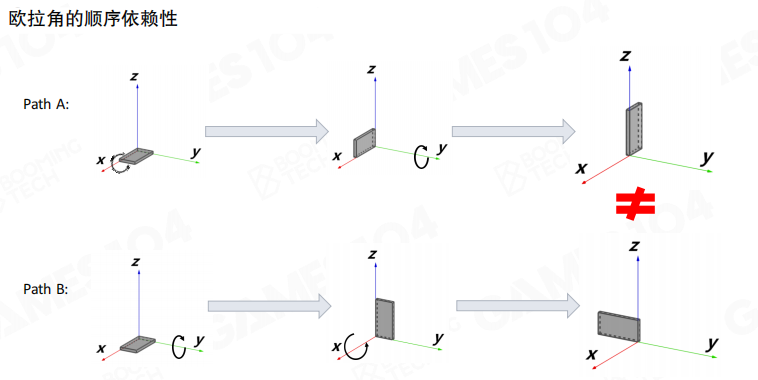
问题示例：对于相同的旋转角度，先绕X轴旋转再绕Y轴旋转，与先绕Y轴旋转再绕X轴旋转，最终得到的结果完全不同。这意味着在使用欧拉角时，必须明确指定旋转顺序（如XYZ、ZYX等），否则会产生歧义。

万向锁（Gimbal Lock）

欧拉角的另一个严重缺陷在于万向锁（Gimbal Lock）：在有些情况下按照欧拉角进行旋转会出现退化的现象，导致物体的旋转会被锁死在某个方向上。

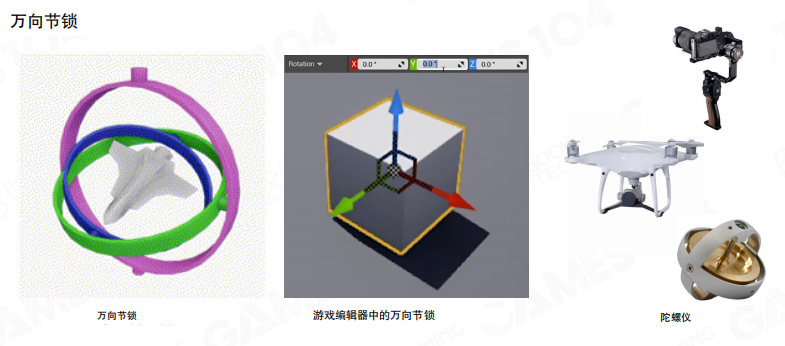
万向锁的产生：当中间轴的旋转角度为90度（或-90度）时，第一个轴和第三个轴的旋转轴会重合，导致失去一个自由度。例如，当俯仰角为90度时，偏航角和滚转角实际上控制的是同一个旋转轴，无法独立控制。

数学上的退化：当β = π/2时，旋转矩阵会退化为只依赖于α - γ的形式，自由度从3个降为1个。这在实际应用中会导致旋转控制失效，特别是在动画插值和物理模拟中。

其他问题

总结欧拉角的主要缺陷：

万向锁及相应的自由度退化问题：在某些角度下会失去一个自由度
很难对欧拉角进行插值：直接对欧拉角进行线性插值会产生不自然的旋转路径
很难通过欧拉角对旋转进行叠加：旋转组合需要转换为旋转矩阵，计算复杂
很难描述绕X、Y、Z轴之外其它轴的旋转：欧拉角只能通过分别绕XYZ轴旋转叠加实现，无法直接表示绕任意轴的旋转

由于这些缺陷的存在，游戏引擎中几乎不会直接使用欧拉角来表达物体的旋转，而是使用更强大的数学工具——四元数（Quaternion）。

四元数（Quaternion）

在游戏引擎中更常用的旋转表达方式是四元数（Quaternion），它由爱尔兰数学家威廉·罗恩·汉密尔顿爵士于1843年提出。

四元数的发现：1843年10月16日，汉密尔顿爵士在都柏林的布鲁姆桥（Broom Bridge）上灵光乍现，发现了四元数乘法的基本公式i² = j² = k² = ijk = -1，并将其刻在桥的石头上。这个发现解决了如何将复数推广到三维空间的问题。

从复数到四元数

我们知道二维空间中的旋转可以使用复数来进行表示。换句话说，二维平面上的旋转等价于复数乘法。

复数的旋转性质：

复数z = a + bi可以表示为向量[a, b]
两个复数的乘积zw的模等于模的乘积：|zw| = |z||w|
两个复数的乘积的角度等于角度的和：arg(zw) = arg(z) + arg(w)
因此，复数乘法等价于旋转和缩放

类似地，我们可以认为四元数是复数在三维空间的推广。一个四元数具有1个实部和3个虚部。

四元数的定义

四元数的定义：

四元数q = a + bi + cj + dk，其中a, b, c, d ∈ R
虚数单位满足：i² = j² = k² = ijk = -1
可以表示为实部和向量两部分的对偶形式：q = (a, v)，其中v = [b, c, d]ᵀ

四元数的基本运算：

范数：||q|| = √(a² + b² + c² + d²)
共轭：q* = a - bi - cj - dk
逆：对于单位四元数（||q|| = 1），有q⁻¹ = q*

四元数的乘积：两个四元数的乘积可以通过矩阵乘法来表示，这使得四元数运算在计算机中实现起来非常高效。

四元数表示旋转

可以证明，任意的三维旋转可以通过一个单位四元数来表示。当我们需要对点进行旋转时，只需要先把点转换成一个纯四元数（实部为0），然后再按照四元数乘法进行变换，最后取出虚部作为旋转后的坐标即可。

四元数旋转公式：

将向量v = [b, c, d]ᵀ转换为纯四元数：v_q = (0, v) = bi + cj + dk
使用单位四元数q进行旋转：v'_q = q * v_q * q* = q * v_q * q⁻¹
旋转后的向量v'就是v'_q的虚部

欧拉角与四元数的转换

进一步可以证明用欧拉角表达的旋转都对应着一个四元数的表示。同样地，四元数与旋转矩阵之间也存在着相应的转换关系。

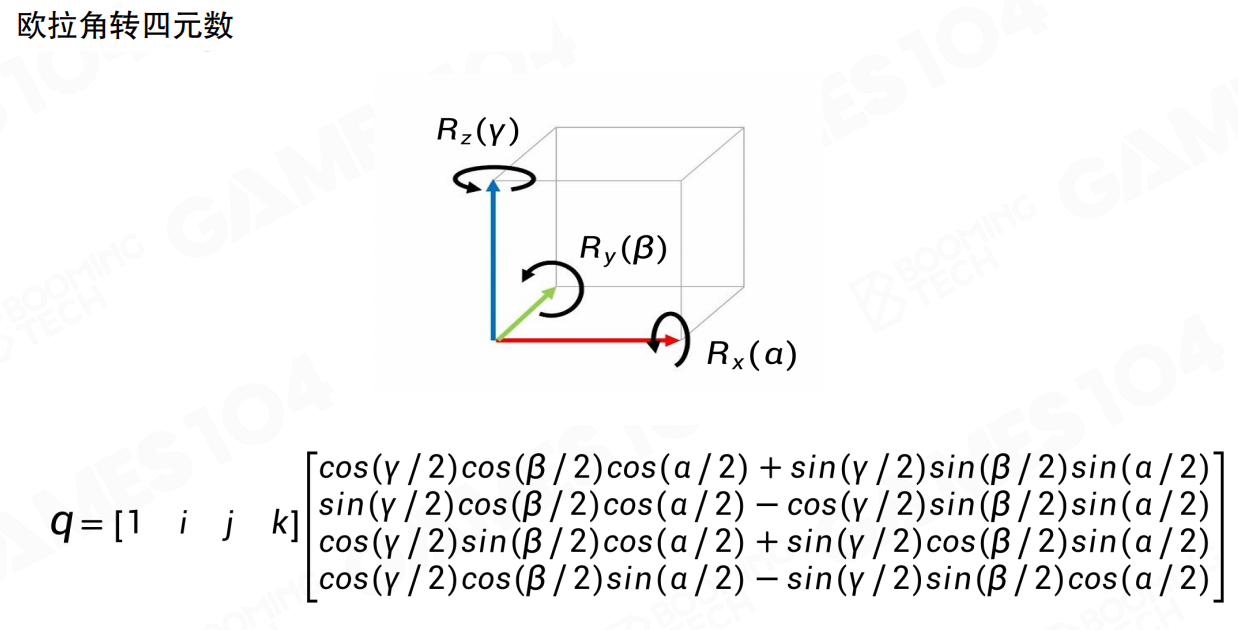
欧拉角转四元数：对于欧拉角(α, β, γ)（分别绕X、Y、Z轴旋转），对应的四元数为：

q = [cos(γ/2)cos(β/2)cos(α/2) + sin(γ/2)sin(β/2)sin(α/2),
     sin(γ/2)cos(β/2)cos(α/2) - cos(γ/2)sin(β/2)sin(α/2),
     cos(γ/2)sin(β/2)cos(α/2) + sin(γ/2)cos(β/2)sin(α/2),
     cos(γ/2)cos(β/2)sin(α/2) - sin(γ/2)sin(β/2)cos(α/2)]

四元数转旋转矩阵：对于单位四元数q = (a, b, c, d)，对应的旋转矩阵为：

R = [[1-2c²-2d²,  2bc-2ad,      2ac+2bd    ],
     [2bc+2ad,     1-2b²-2d²,    2cd-2ab    ],
     [2bd-2ac,     2ab+2cd,      1-2b²-2c²  ]]

四元数的优势

使用四元数来表达三维旋转的优势在于我们可以使用简单的代数运算来获得旋转的逆运算、旋转的组合以及两个单位向量之间的相差的旋转量。

旋转组合：

对于两个旋转q₁和q₂，组合旋转为：v'' = q₂ * (q₁ * v * q₁*) * q₂* = (q₂q₁) * v * (q₂q₁)*
这意味着组合旋转只需要四元数乘法，比矩阵乘法更高效

旋转的逆：

旋转的逆就是四元数的共轭：q⁻¹ = q*（对于单位四元数）

两个单位向量之间的旋转：

给定两个单位向量u和v，可以构造四元数q来表示从u到v的旋转

绕任意轴旋转

对于绕任意轴旋转的情况，我们同样可以利用旋转轴和旋转角度的信息来构造出四元数进行表达。

绕单位轴旋转：

对于向量v，绕单位轴u = [xu, yu, zu]ᵀ旋转角度θ，旋转四元数为：
- q = (cos(θ/2), sin(θ/2) * xu, sin(θ/2) * yu, sin(θ/2) * zu)
旋转后的向量：v'_q = q * v_q * q*

这使得四元数可以轻松表示绕任意轴的旋转，而欧拉角只能通过分别绕XYZ轴旋转叠加实现。

总结

欧拉角 vs. 四元数：

特性	欧拉角	四元数
直观性	直观易懂	数学抽象
万向锁	存在	不存在
插值	困难	简单（球面线性插值）
旋转组合	需要矩阵	直接乘法
绕任意轴旋转	困难	简单
存储空间	3个浮点数	4个浮点数

四元数能够很好地处理旋转计算的矩阵运算，使用十分方便、优雅。引擎中通常会给到简单易用的接口，但四元数的数学思想并不容易理解。总体来说，四元数将三维的旋转与角度映射到四维空间中处理，通过牺牲一个维度的直观性，换来了数学上的优雅和计算上的高效。

在游戏引擎中，四元数是表示旋转的标准方式，它完美解决了欧拉角的所有问题，是现代3D图形学和游戏开发的基础工具。

8.6 蒙皮动画的实现：关节与蒙皮

有了三维旋转的表达方法后，我们就可以利用关节的姿态来控制角色模型的运动。下面我们来看看关节姿态和蒙皮的具体实现。

关节姿态（Joint Pose）

骨骼动画处理和一般对象的处理一样，包括角度、位置和缩放变化。每个关节的姿态可以分为三个部分：

朝向（Orientation）：旋转改变关节的朝向。大多数骨骼姿态只改变关节的朝向。当旋转一个关节时，该关节及其所有子关节的局部坐标系都会跟着旋转。

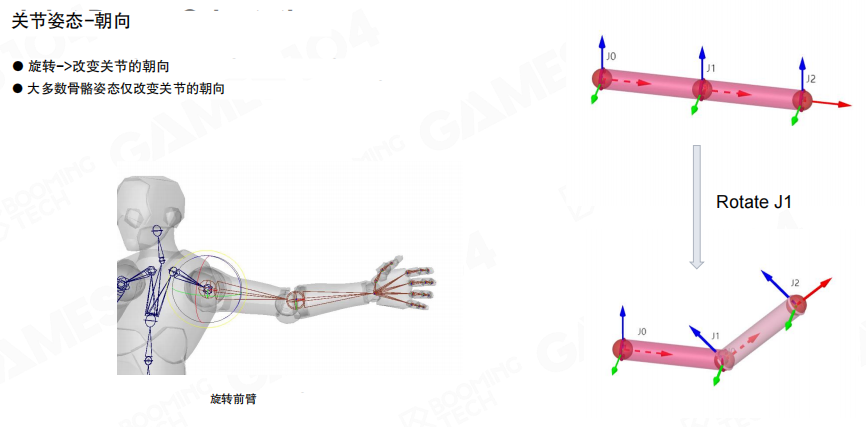
位置（Position）：平移改变位置。通常在人形骨骼中不会改变，除了骨盆、面部关节和其他特殊关节。位置变换主要用于拉伸模型，比如角色移动时根关节的平移，或者面部关节的平移来产生表情。

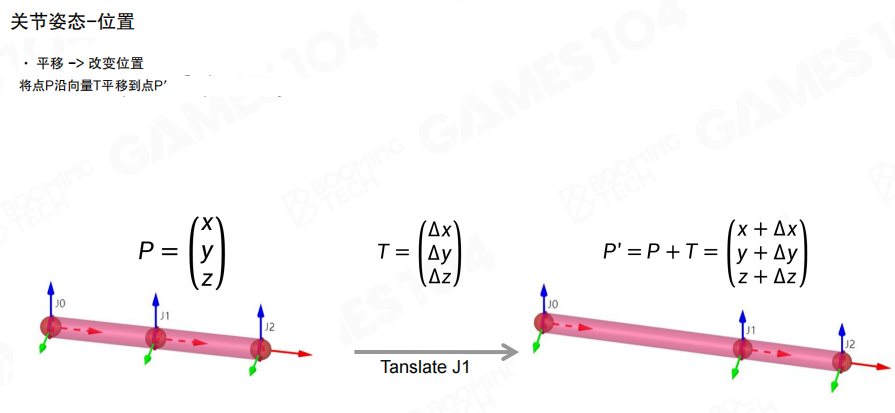
缩放（Scale）：缩放改变模型的大小。有均匀缩放和非均匀缩放两种。缩放广泛应用于面部动画，比如眼睛的等比缩放和鼻子的非均匀缩放。

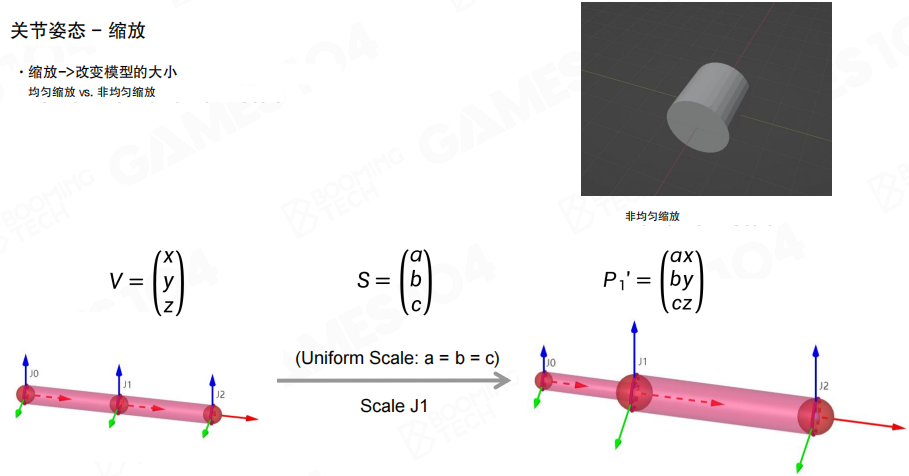
仿射矩阵（Affine Matrix）：把平移、旋转和缩放组合到一起，就可以通过一个仿射矩阵来描述关节的姿态。对于骨骼上的每一个关节，我们实际上只需要存储它相对于父节点的相对姿态。这样在计算绝对姿态时可以利用仿射矩阵的传递性从根节点出发进行累乘即可。

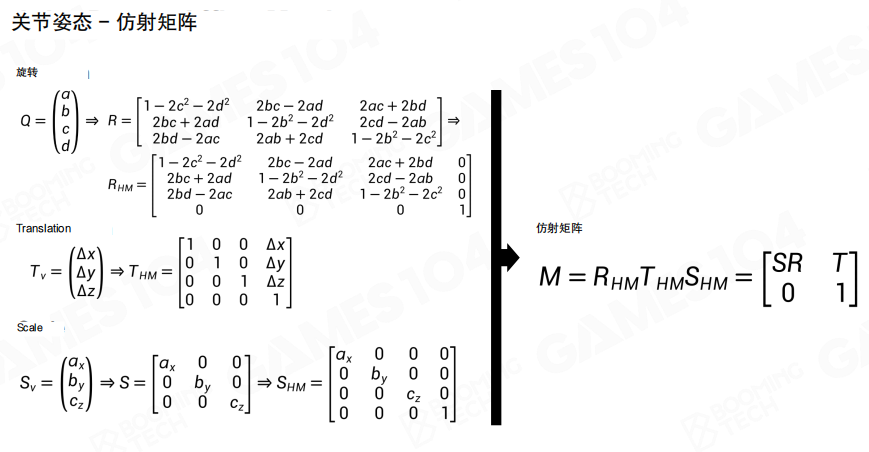
局部空间到模型空间

对于蒙皮网格中的关节j，记p(j)为关节j的父关节，M’p(j)为关节j的父关节在局部空间中的姿态。关节J在模型空间中的位姿M^m可以通过从J到根遍历骨架层次结构来计算：

M^m_J = ∏(从j=J到0) M'_p(j)

这种利用相对坐标系来描述位姿关系的好处在于它可以正确地对角色动作进行插值，而如果直接从绝对坐标系进行插值则会得到错误的结果。

在局部空间中进行插值，使用增量变换所需数据量更少，便于插值或混合。而在模型空间中直接插值不适合，因为会导致不自然的运动路径。

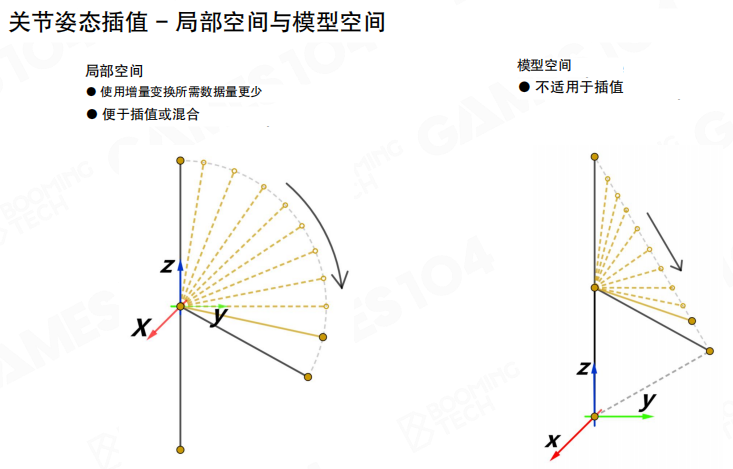
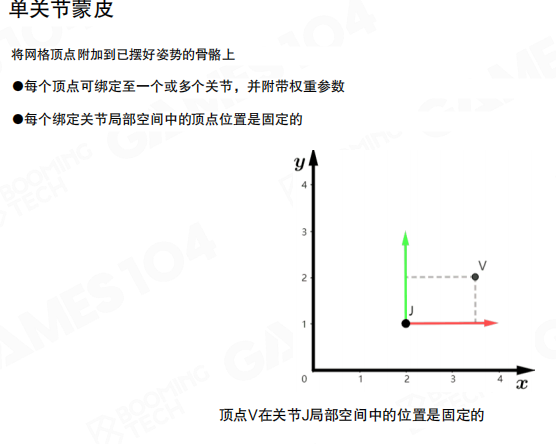
单关节蒙皮

将网格顶点附加到已摆好姿势的骨骼上。每个顶点可绑定至一个或多个关节，并附带权重参数。每个绑定关节局部空间中的顶点位置是固定的。

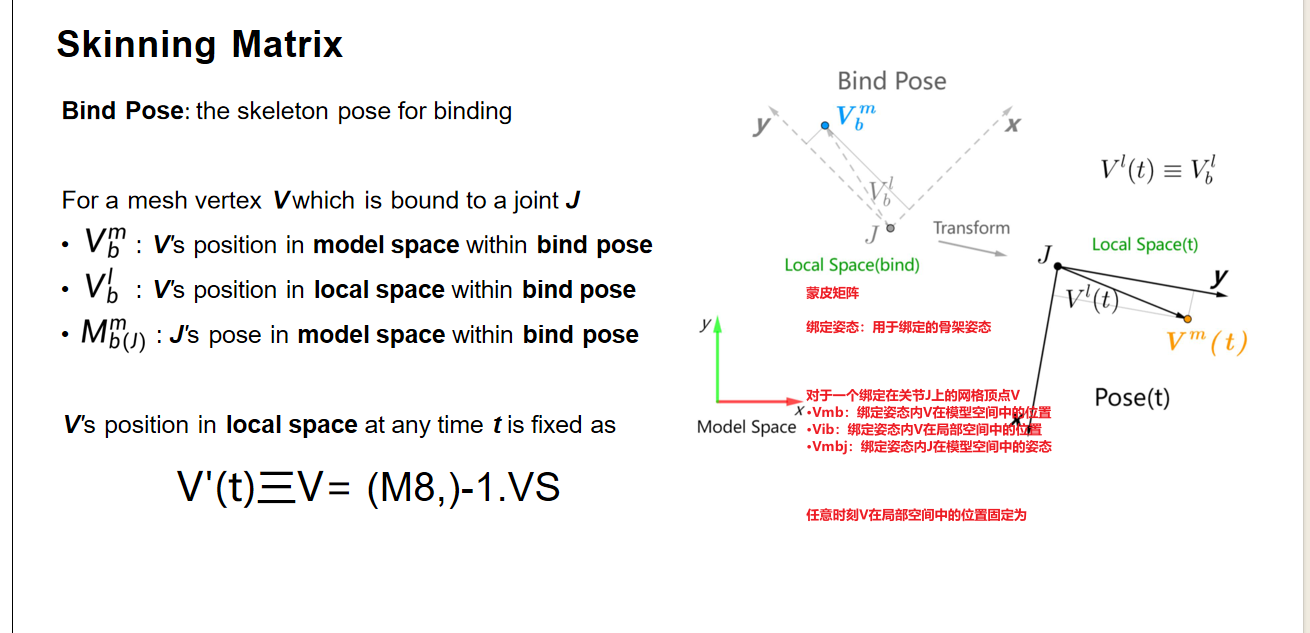
蒙皮矩阵（Skinning Matrix）

记顶点V在关节J定义的局部坐标系下的坐标为V^l_J，初始时刻进行绑定时V在模型坐标系下的坐标为V^m_b。在时刻t，当关节位姿发生变化后顶点的局部坐标保持不变。此时顶点在模型坐标系下的坐标V^m(t)与初始时刻模型坐标系下绑定的坐标V^m_b之间的变换关系为：

V^m(t) = M^m_J(t) · (M^m_b(J))^-1 · V^m_b

其中K = M^m_J(t) · (M^m_b(J))^-1称为关节J的蒙皮矩阵（skinning matrix）。注意到蒙皮矩阵的第二项包含矩阵求逆运算，在游戏引擎中为了提高计算效率一般会直接存储整个逆阵，即逆绑定姿势矩阵。

骨骼在内存中的表示：每个关节存储关节名称（可以是字符串形式或哈希化的32位字符串ID）、该关节在骨架中的父节点索引、绑定姿势的平移、旋转和缩放，以及逆绑定姿势变换矩阵。

蒙皮矩阵调色板：每个关节的蒙皮矩阵数组，用于在着色器中由GPU使用。优化时，可以计算模型空间到世界空间的变换矩阵M^W，关节J的优化蒙皮矩阵为：

K'_j = M^W · M^m_j(t) · (M^m_b(J))^-1

多关节加权蒙皮

对于绑定到N个关节的网格顶点V，每个绑定关节都有对应的蒙皮权重Wi，且所有权重之和为1：

Σ(i=0到N-1) Wi = 1

顶点V在模型空间中的位置是它在每个关节上定义的局部坐标转换到模型坐标后的加权和：

V^m(t) = Σ(i=0到N-1) Wi · V^m_i(t)

其中V^m_i(t) = K_i(t) · V^l_b(J_i)是顶点V通过关节Ji的蒙皮矩阵变换后的位置。

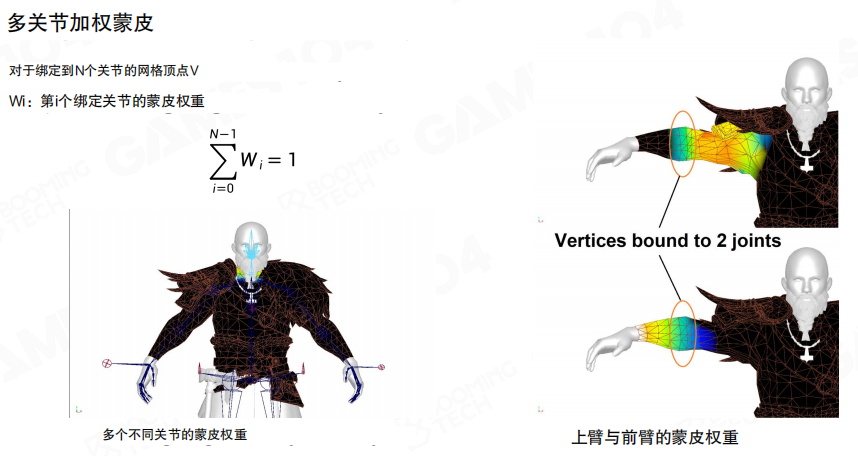
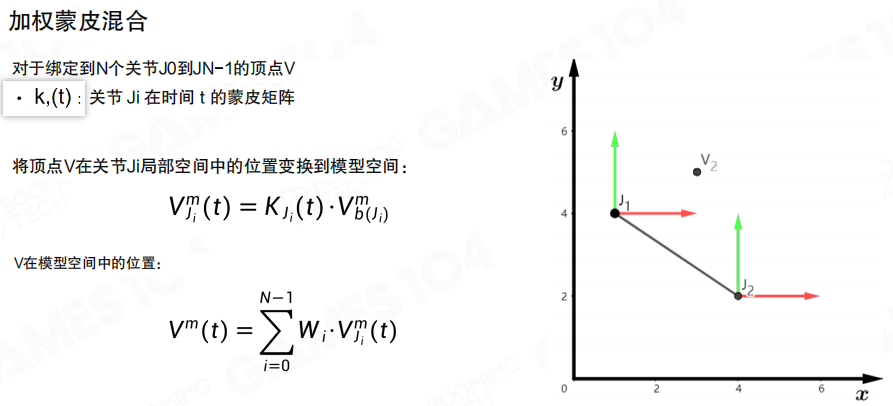
关节附近的顶点通常绑定到相邻的两个骨骼，比如肘关节附近的顶点会同时受到上臂和前臂的影响，通过权重混合实现平滑的变形。

动画插值

一个动画片段（Clip）是由一系列骨骼姿态组成的。动画的时间线是连续的，但实际制作时只会记录关键帧，关键帧之间需要通过插值来计算过渡姿态。

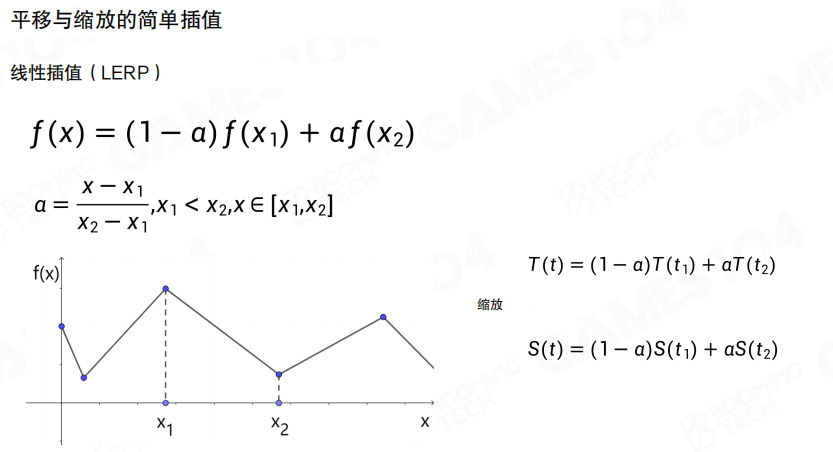
平移与缩放的线性插值（LERP）：对于平移和缩放，可以直接使用线性插值：

f(x) = (1 - a)f(x1) + a·f(x2)

其中a = (x - x1) / (x2 - x1)，x1 < x2，x ∈ [x1, x2]。

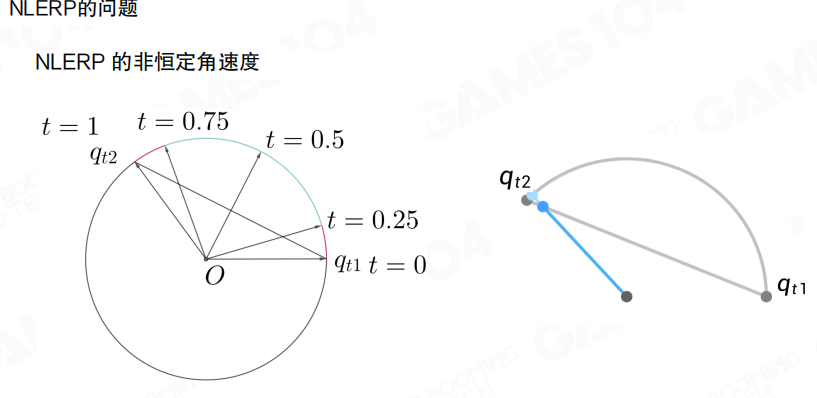
四元数旋转插值：对于旋转，情况要复杂一些。最直观的方法是线性插值，但旋转需要保证半径不变，因此要对线性插值结果进行归一化处理，这就是NLERP（归一化线性插值）：

qt = Nlerp(qt1, qt2, t) = ((1-a)qt1 + a·qt2) / ||(1-a)qt1 + a·qt2||

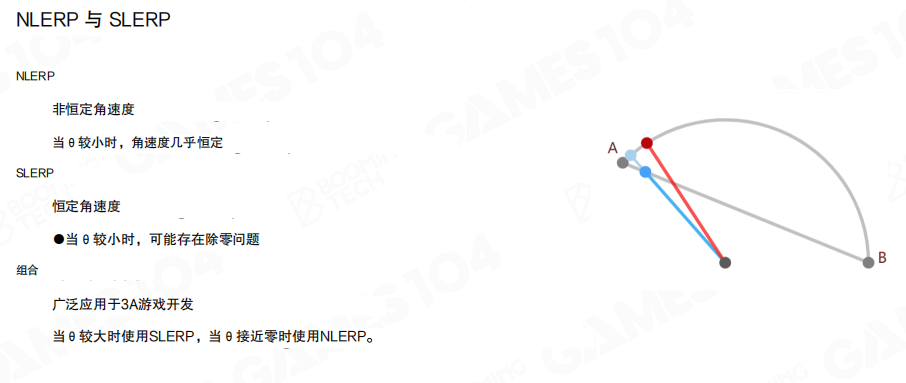
NLERP的问题是非恒定角速度，当角度较小时角速度几乎恒定，但当角度较大时会有明显的违和感。

最短路径修正：从一个角度移动到另一个角度，对于每个维度来说都有两种变化方式，符合人直观的插值是最短路径插值。通过四元数点乘的正负值来判断旋转方向：

如果qt1 · qt2 ≥ 0：qt = ((1-a)qt1 + a·qt2) / ||(1-a)qt1 + a·qt2||
如果qt1 · qt2 < 0：qt = ((1-a)qt1 - a·qt2) / ||(1-a)qt1 - a·qt2||

SLERP（球面线性插值）：先计算旋转角度，对角度进行插值计算位置。SLERP的公式为：

qt = Slerp(qt1, qt2, t) = (sin((1-t)θ) / sin(θ)) · qt1 + (sin(tθ) / sin(θ)) · qt2

其中θ = arccos(qt1 · qt2)。SLERP的优点是恒定角速度，变化均匀。缺点是计算量略高（需要反三角函数），而且当旋转角度很小时，计算结果不稳定（可能存在除零问题）。

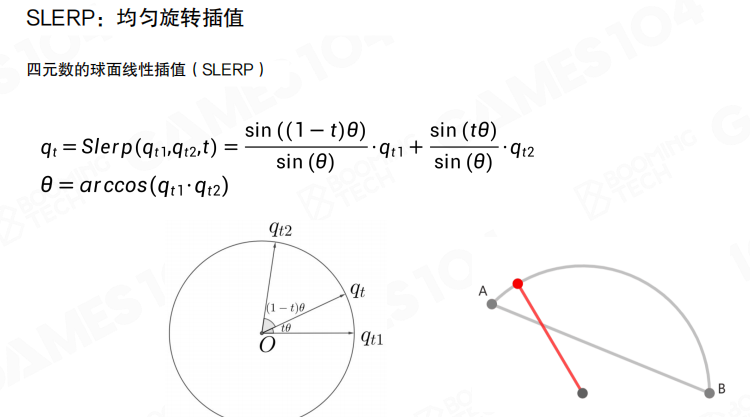
混合处理：设定一个角度阈值，当夹角小于阈值时使用NLERP，当角度大于阈值时使用SLERP。这种方法广泛应用于3A游戏开发，既保证了插值质量，又兼顾了计算效率。

动画运行时管线

我们把上面介绍过的算法整理一下就得到了一个简单的蒙皮动画管线：

提取（Extract）：根据Clip和时间，提取前一帧和后一帧的关键帧数据
插值（Interpolate）：在局部空间中对关键帧进行插值，得到当前时刻的局部姿态
计算蒙皮矩阵（Calculate Skinning Matrix）：从局部空间到模型空间，计算每个关节的蒙皮矩阵，生成蒙皮矩阵调色板
蒙皮（Skinning）：在GPU上使用蒙皮矩阵调色板，对网格顶点进行加权变换，得到最终的顶点位置

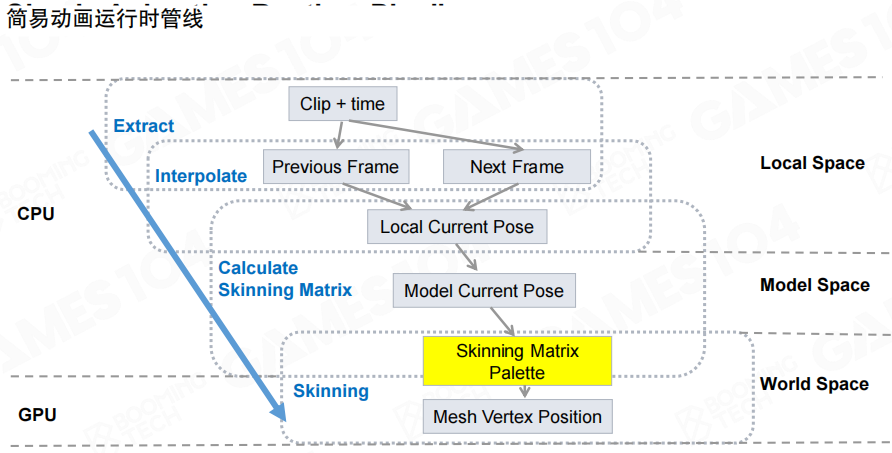
现代游戏引擎开始倾向把动画管线更多的运算交给GPU完成，充分利用GPU的并行计算能力，大幅提升动画处理的性能。

8.7 动画压缩技术

动画需要处理的数据很多，会占用大量的存储空间。如果不进行压缩处理，很难在硬件设备上运行。动画压缩本质来说是用时间换空间，通过压缩减少存储空间，但需要在解压时花费一些计算时间。

动画数据量

动画片段拆分为独立的关节姿态序列，每个关节的姿态序列又可以拆分为独立的平移、旋转和缩放轨道。每个关节每帧需要存储这些数据。

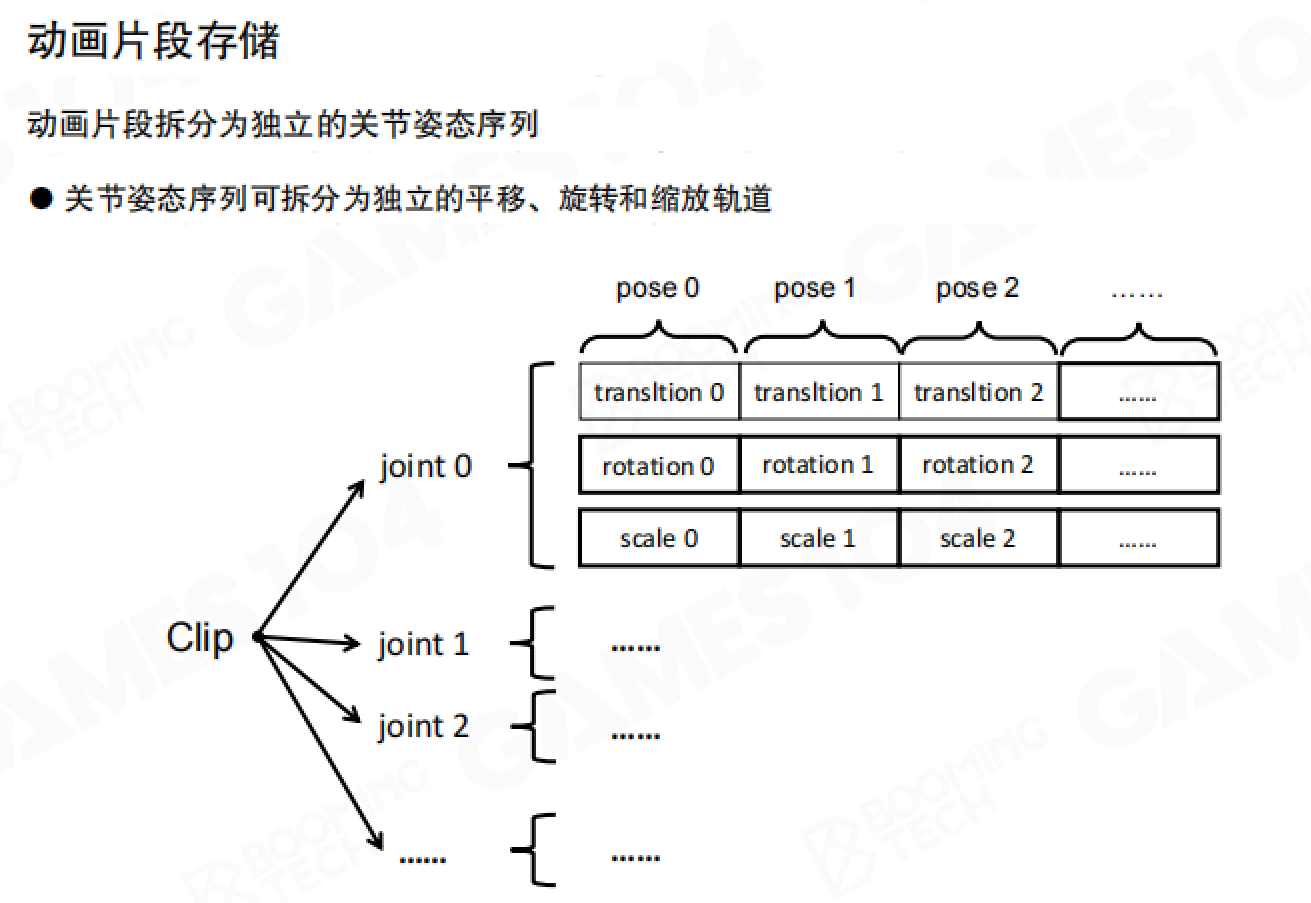
以30帧/秒的动画为例，每帧每个关节需要存储：缩放（3×float）、平移（3×float）、旋转（4×float），共40字节/帧。对于50-100个关节的角色，每秒动画需要58.59-117.19KB的存储空间。

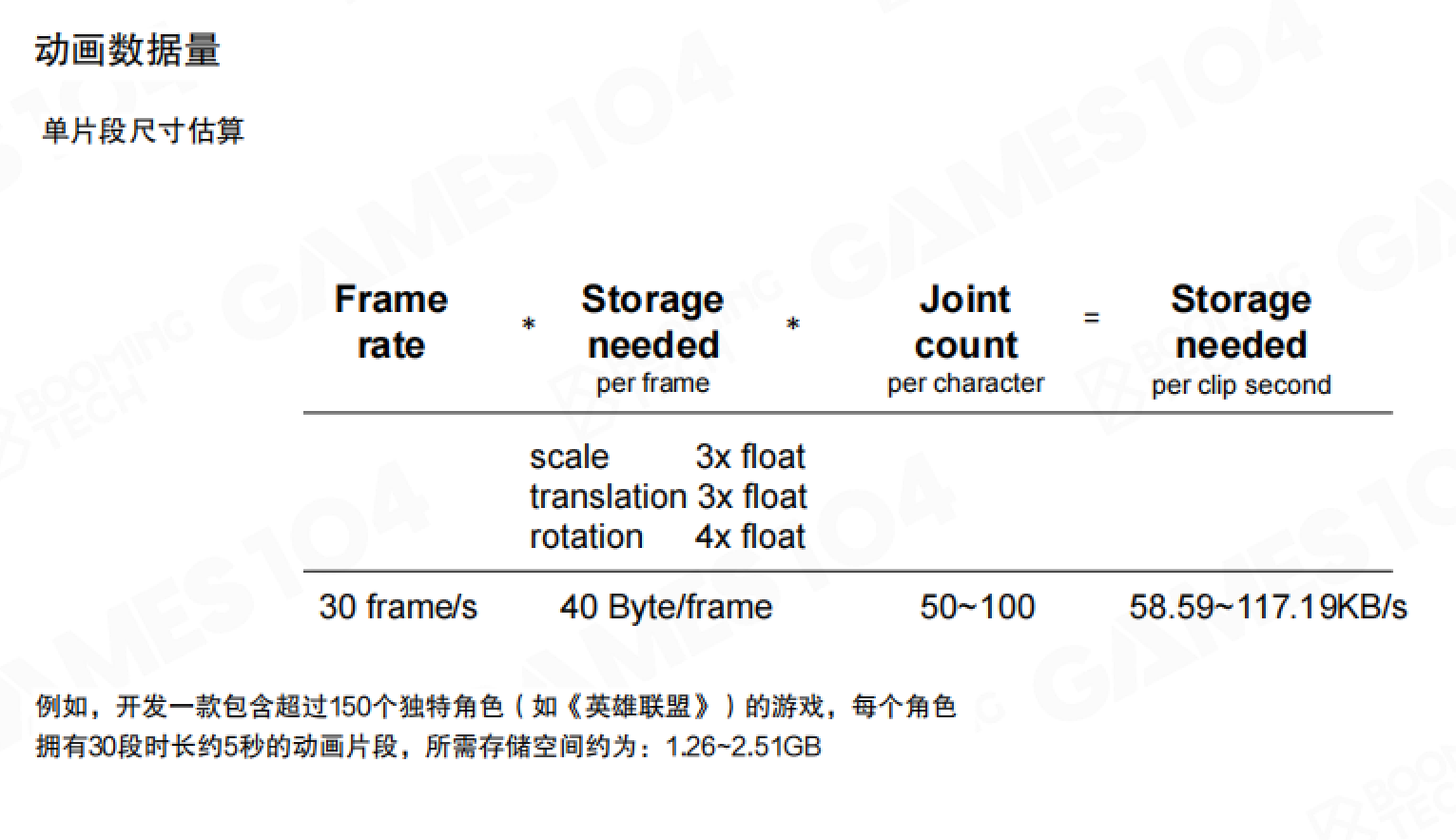
例如，开发一款包含超过150个独特角色的游戏（如《英雄联盟》），每个角色拥有30段时长约5秒的动画片段，所需存储空间约为1.26~2.51GB。如果不进行压缩，这个数据量是难以接受的。

减少不必要的数据

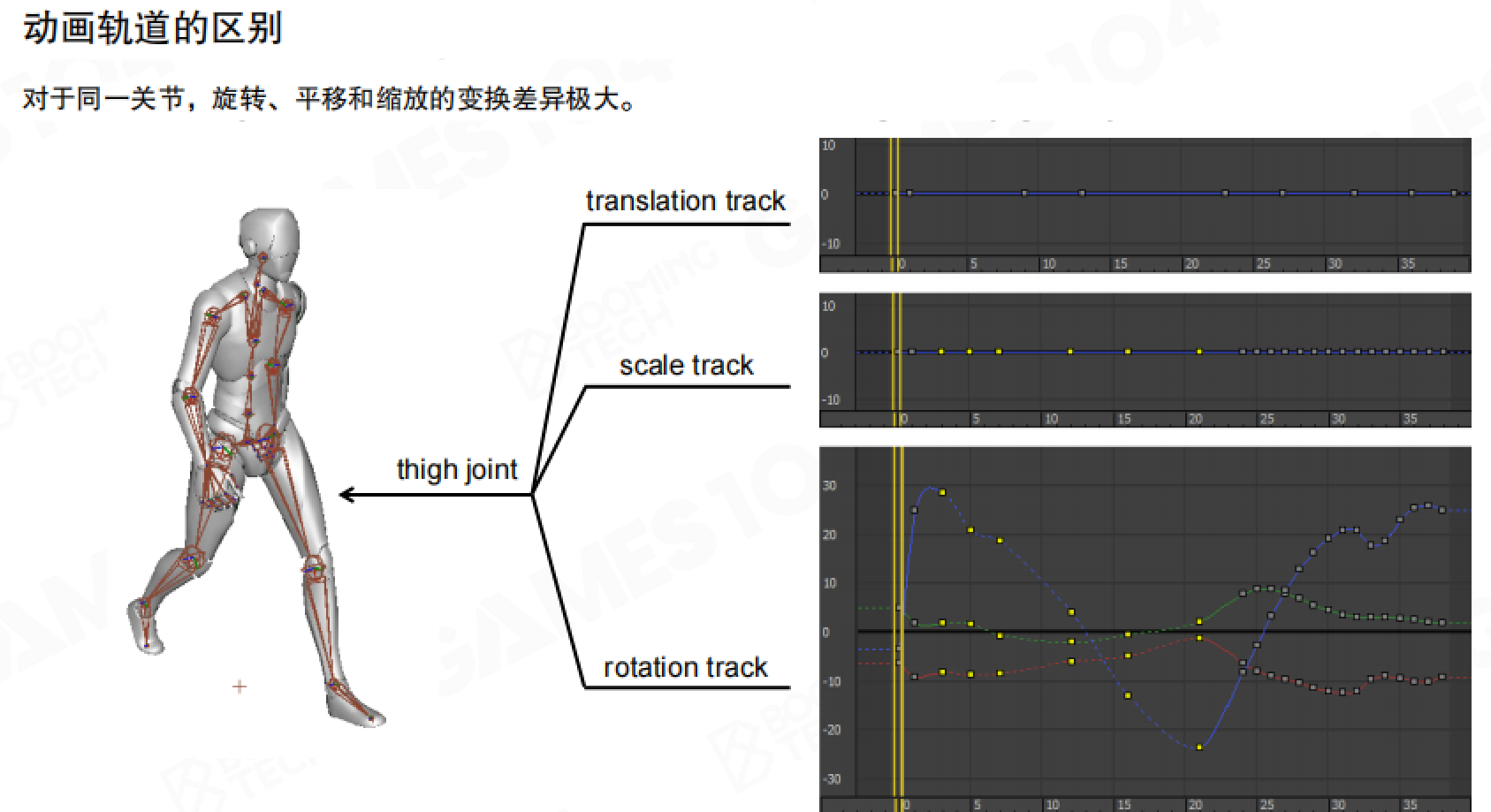
在广泛的实践中，人们发现不同关节、不同自由度的信号之间有着巨大的差异。对于同一关节，旋转、平移和缩放的变换差异极大。以大腿关节为例，在大多数情况下它的缩放自由度都是1，大部分的平动自由度都是0，它的运动基本都来自于旋转。

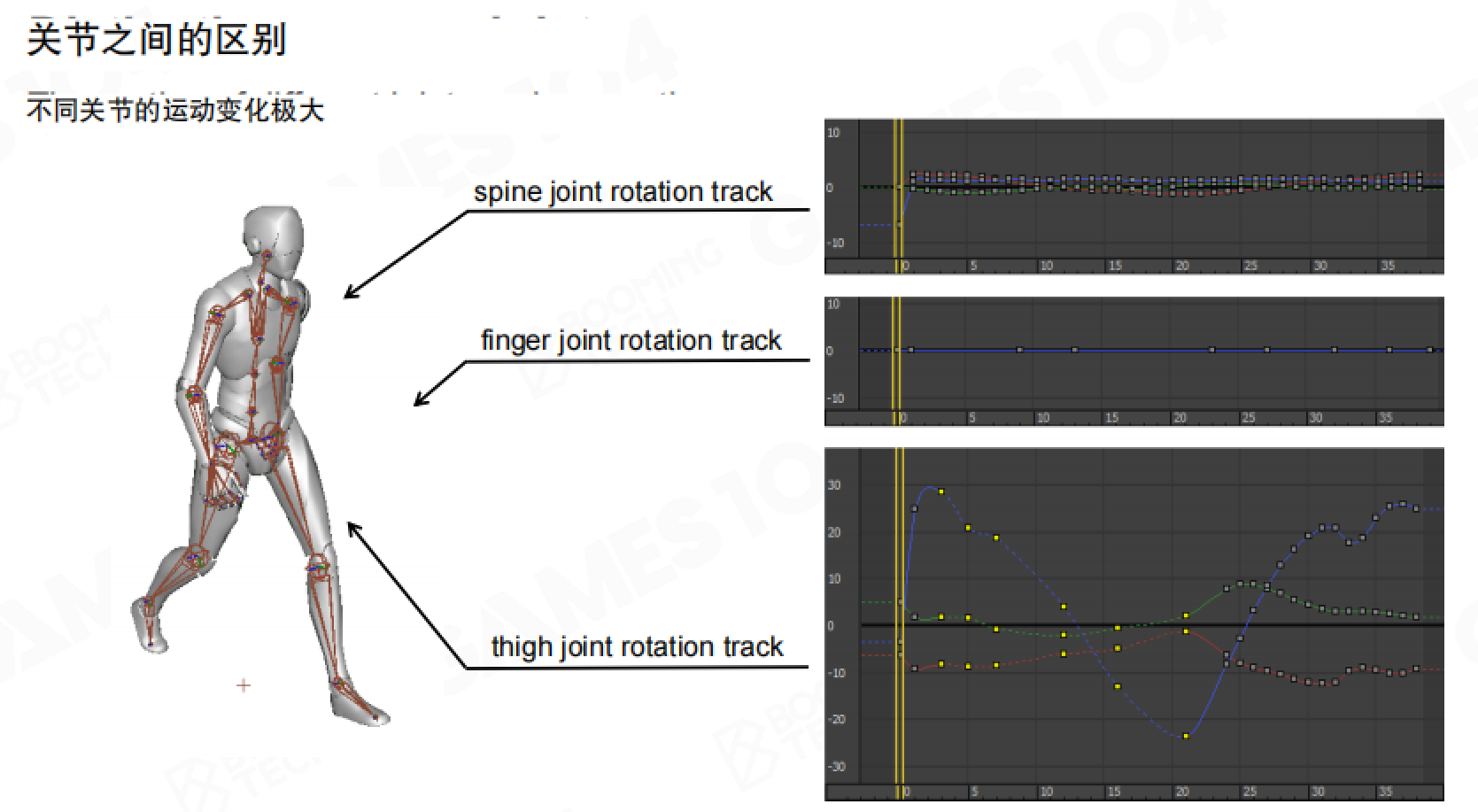
不同关节的运动变化也极大。比如脊柱关节的旋转变化很小，手指关节的旋转也很少，但大腿关节的旋转变化非常大。

因此最简单的动画压缩方法是直接缩减运动的自由度：忽略缩放轨道（在人形骨骼中通常不会改变，除了面部关节），舍弃平移轨道（在人形骨骼中通常不会改变，除了骨盆、面部关节和其他特殊关节）。这样可以把关节的缩放和平动自由度直接去掉，只保存旋转。

关键帧与插值曲线

动画与电影制作中的关键帧（key frame）是指定义任何平滑过渡起始点和结束点的绘图或镜头。一个动画片段是由一系列骨骼姿态组成的，但实际制作时只会记录关键帧，关键帧之间需要通过插值来计算过渡姿态。

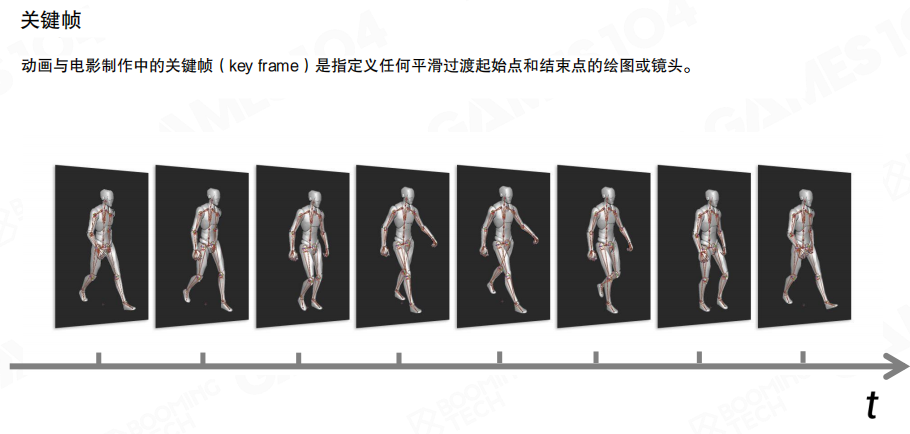
对于旋转自由度，我们可以使用关键帧来对信号进行离散，然后通过插值来重建原始信号。在离散时还可以利用不等间距采样的方式来进一步压缩信号。

线性关键帧简化：移除那些可以通过相邻帧线性插值拟合的帧。对于每个帧i，计算frame[i-1]和frame[i+1]的线性插值，然后计算与frame[i]的误差。如果误差在可接受范围内，就可以移除这个帧。

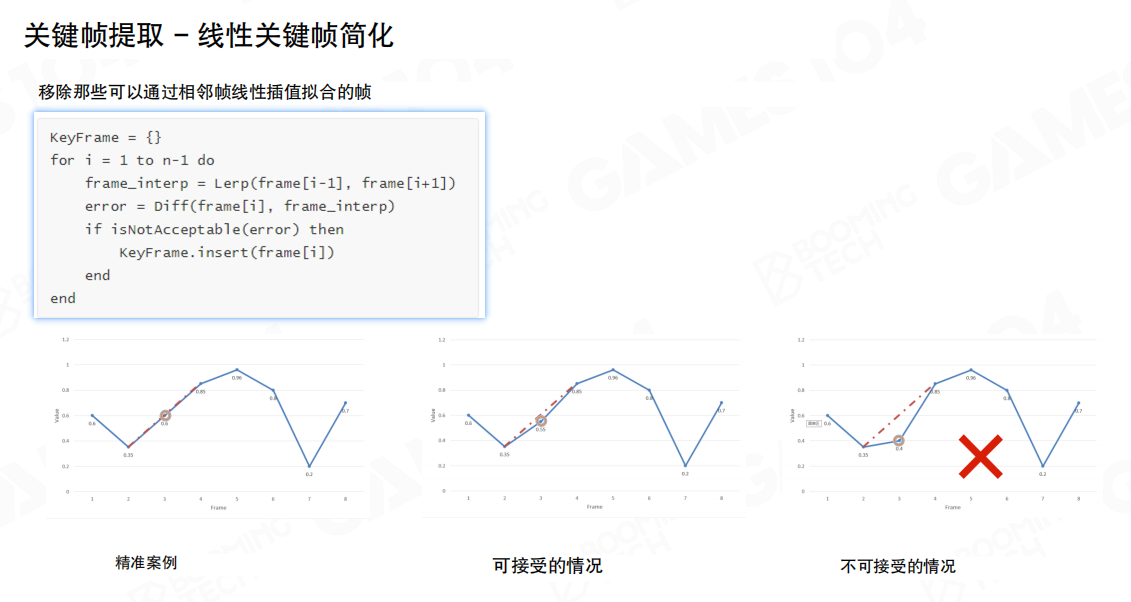
Catmull-Rom样条：直接使用线性插值来描述非等间距采样的旋转信号仍然不够自然，这里推荐使用Catmull-Rom曲线来对关键帧进行插值。Catmull-Rom曲线只需要一个锐度参数α（通常取α=0.5）以及4个控制点就可以获得C1连续的光滑曲线。

Catmull-Rom样条的拟合过程是：以原始曲线的两端作为中间两个控制点，创建一条Catmull-Rom样条曲线。通过类似二分查找的方式迭代添加控制点，通过最邻近的4个点计算内曲线，重复此过程直到每一帧的误差均低于阈值。

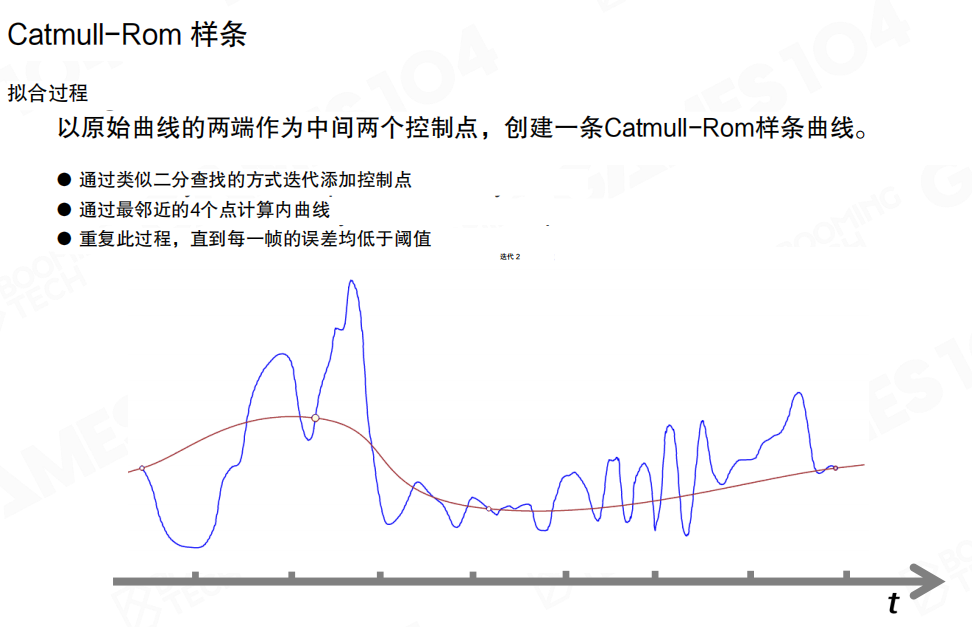
基于Catmull-Rom曲线可以实现非常高精度的信号离散和重建效果。

数值精度（量化）

进一步压缩数据时，还可以考虑使用低精度的存储方式来记录位移信号。量化的关键在于找到合适的误差阈值，并尽可能使用更少的存储位数。

浮点量化：使用较少位数的整数来表示有限范围和精度的浮点数值。所需位数 = ⌈log₂(范围/精度)⌉。例如，平移范围[0,10]，精度0.001米，需要⌈log₂(10/0.001)⌉ = 14位。通常而言，16位精度足以满足游戏引擎中姿态数据的浮点数范围与精度要求。

浮点数量化的过程是：将原始值位于固定范围[-50.5, 112.5]内，对原始值进行归一化处理到[0,1]范围，然后将[0,1]范围重新映射到[0,65535]，每个数值代表0.00001525…的步进值。

四元数量化：对四元数进行压缩时，可以利用单位四元数每一位上数值的范围来进行化简。用三个数即可表示单位四元数，例如q = (a, b, c, √(1-(a²+b²+c²)))。剩余三个数的取值范围可限定在[-1/√2, 1/√2]区间内，若始终省略绝对值最大的数。

四元数量化的存储方案：使用2比特位表示被舍弃的数字（指定X、Y、Z、W中绝对值最大的分量），每个数值使用15位存储，范围在[-1/√2, 1/√2]内，精度为√2/32767≈0.000043。最终，四元数可存储在48位存储空间中，从128位压缩而来。

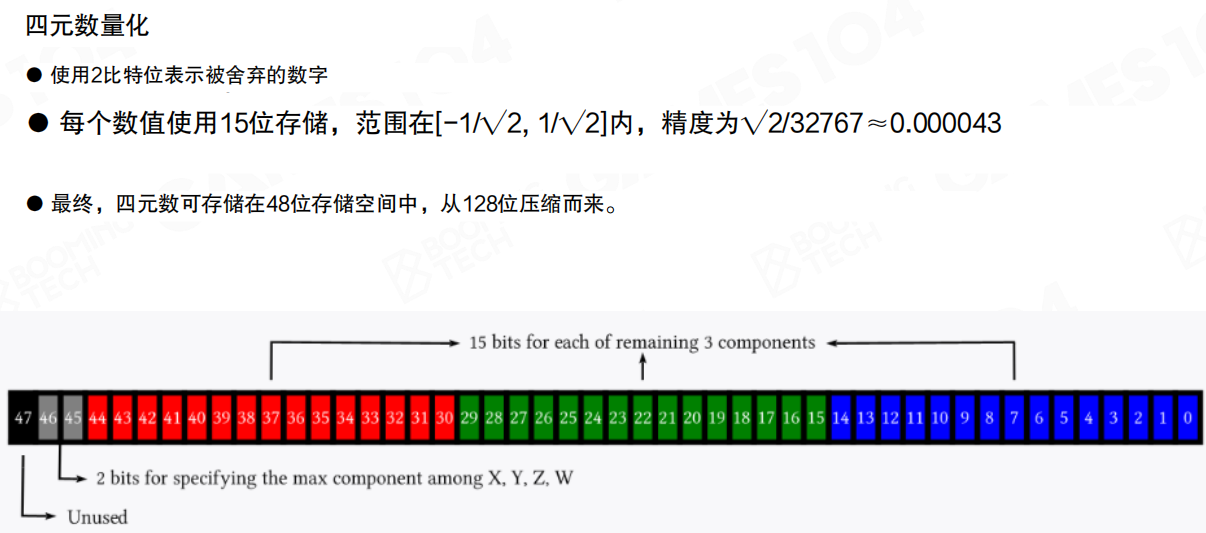
量化导致的尺寸缩减：每帧关节位姿从32字节（缩放1×float、平移3×float、旋转4×float）压缩到14字节（缩放16位、平移48位、旋转48位）。关键帧技术与量化方法可结合使用，以获得更高的压缩比。

误差处理

数据压缩必然会导致精度损失的问题。动画压缩本质来说是用时间换空间，数据在压缩和解压过程中就可能存在信息失真的情况。

误差传播：动画数据压缩导致的误差会在骨骼之间累积。骨骼存储局部空间变换数据，骨骼通过层级结构进行组织。对于末端的关节，由于误差传播的效应可能会产生非常大的累计误差，这种现象的直观反映就是模型可能会产生视觉上可见的偏移。

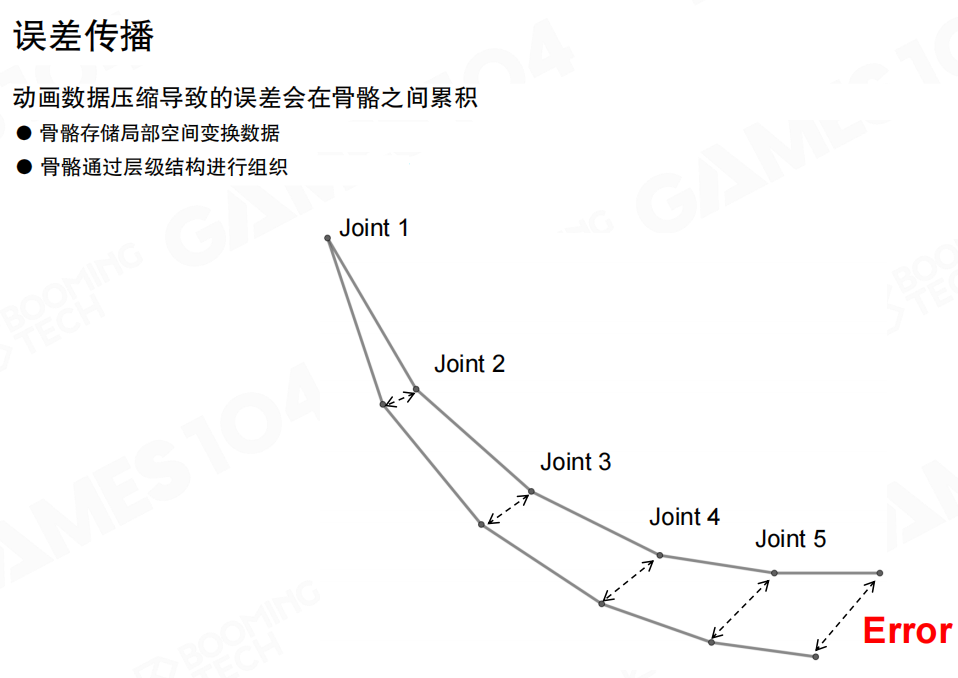
关节对误差的敏感性：某些特殊部位需要高精度动画，比如手部握持武器、面部表情等关键部位。这些部位对误差非常敏感，需要更高的精度。

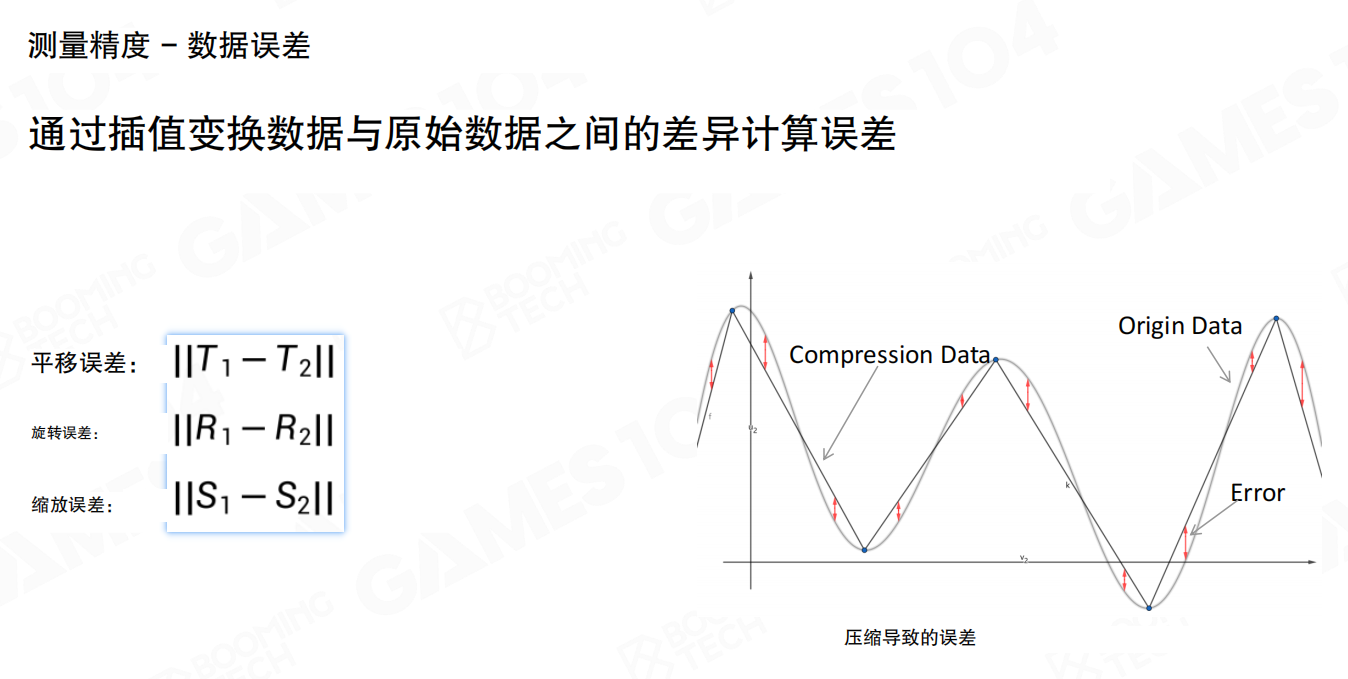
测量精度：要缓解累计误差，首先需要定量化地描述误差。通过插值变换数据与原始数据之间的差异计算误差：平移误差||T1-T2||、旋转误差||R1-R2||、缩放误差||S1-S2||。

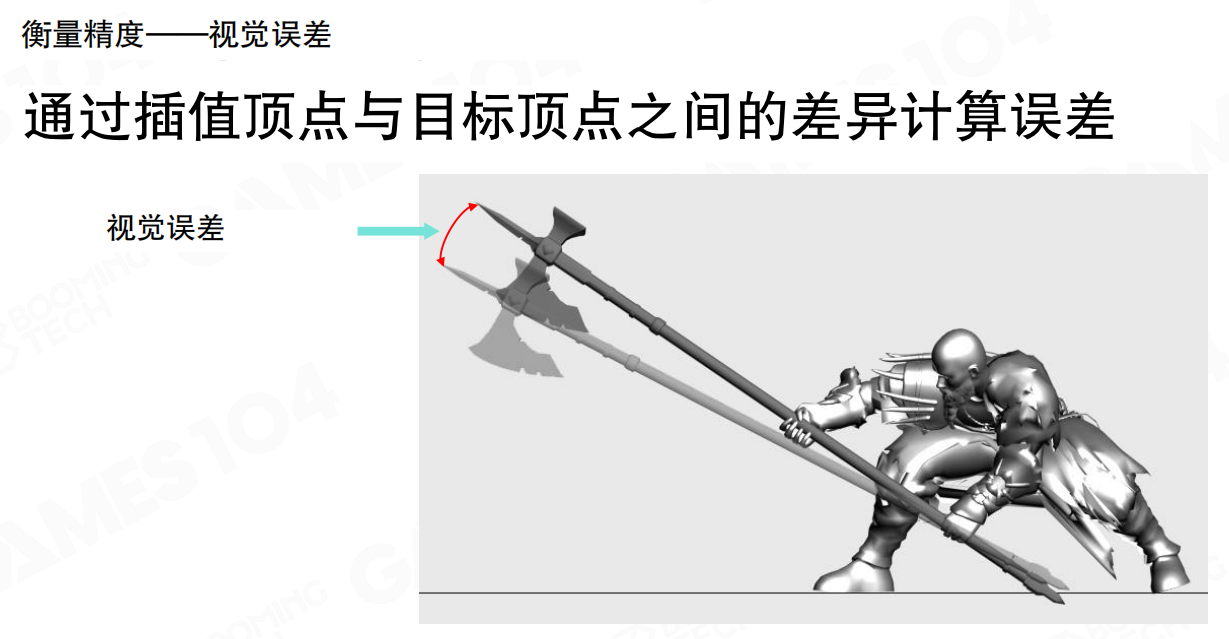
视觉误差：通过插值顶点与目标顶点之间的差异计算误差。计算每个顶点的视觉误差计算量巨大，因此工业界的主流处理方法是在关节上设置虚拟顶点（fake vertices），然后利用虚拟顶点压缩前后的差异来描述误差。

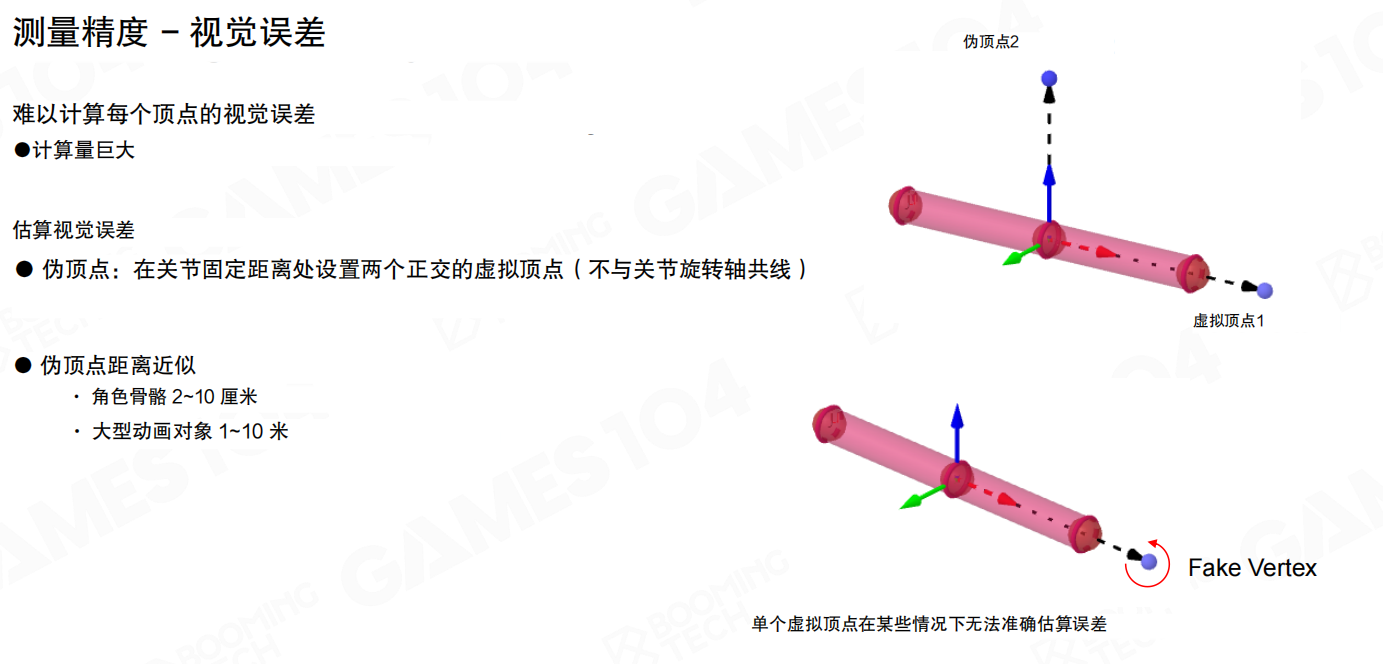
伪顶点在关节固定距离处设置两个正交的虚拟顶点（不与关节旋转轴共线）。伪顶点距离近似：角色骨骼2~~10厘米，大型动画对象1~~10米。单个虚拟顶点在某些情况下无法准确估算误差，因此需要两个正交的虚拟顶点。

误差补偿：要缓解累计误差，我们可以为不同的关节设置不同的存储精度，或是通过主动补偿的方式来进行修正。

自适应误差容限：对从末端到根部的不同关节采用差异化的精度阈值，以降低由父关节引起的误差。最大误差阈值设为t，末端关节（如脚趾）使用t，越靠近根部的关节（如大腿）使用越小的阈值（t/2、t/3、t/4），要求更高的精度。

原位修正：在除根骨骼外的每根骨骼上选择一个点，从根骨骼开始计算每个压缩骨骼的旋转，使标记点最接近其在模型空间中的实际位置，将旋转量叠加到压缩数据的变换矩阵中。优点是由于所有数据已在压缩期间计算完成，解压过程不会产生额外开销。缺点是可能因对关键帧的修改而产生内存开销，可能产生噪声轨迹，压缩可能耗费更多时间。

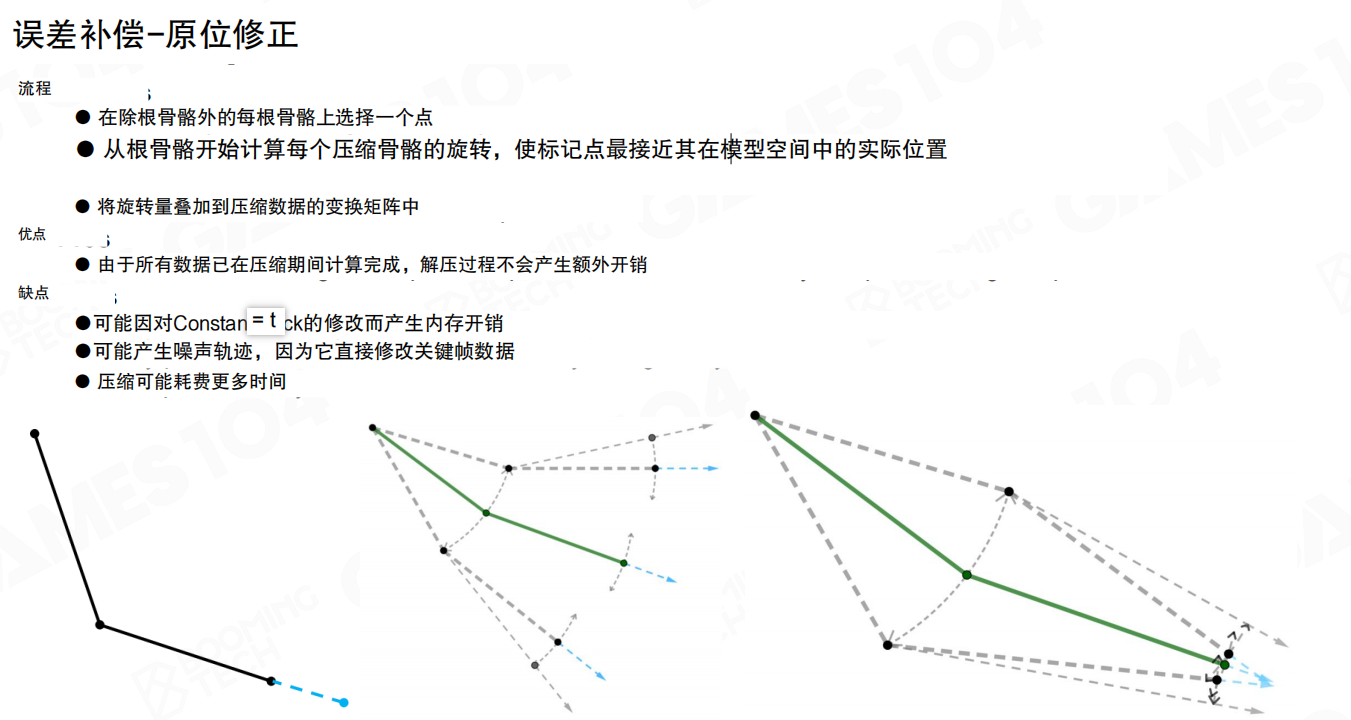
总体而言，对于累计误差目前没有非常完善的处理方法，需要在压缩比和精度之间找到平衡。

8.8 动画制作流程

动画制作是游戏开发中至关重要的环节，从最初的模型建立到最终的动画导出，整个流程涉及多个专业环节的协同工作。现代游戏中的角色动画通常采用数字内容创作（DCC, Digital Content Creation）流程，通过专业的3D建模软件完成从模型到动画的全流程制作。

通常，动画DCC流程包括以下主要步骤：网格构建（Mesh Building）、骨骼绑定（Skeleton Binding）、蒙皮（Skinning）、动画创作（Animation Creation）和导出（Exporting）。每个步骤都有其特定的技术要求和注意事项。

网格构建（Mesh Building）

动画制作的第一步是建立网格模型。建模师设计的三维模型通常具有远高于动画需求的精度，因此在动画制作阶段往往只会使用低精度模型进行处理，以降低计算负担和提高制作效率。

网格构建通常包括四个主要阶段：

粗模阶段（Blockout Stage）：创建角色的粗略轮廓，确定基本的比例和形状。这个阶段主要关注整体结构，不追求细节精度。
高模阶段（High-poly Stage）：提升模型精度，添加细节和表面特征。高模通常用于烘焙法线贴图等细节信息，但不会直接用于动画制作。
低模阶段（Low-poly Stage）：将表面分割成适合动画的网格结构。这是动画制作中实际使用的模型，需要合理的拓扑结构以支持骨骼变形。
纹理阶段（Texturing Stage）：为角色添加纹理和材质，完成视觉外观的制作。

关节处网格加密：为了保证最终动画成品的效果，建模师在建模时一般会在关节处对网格进行加密。关节区域（如肘部、膝盖、肩部）需要更多的顶点和面片，以确保在骨骼旋转时能够产生平滑自然的变形效果。如果关节处的网格过于稀疏，动画效果会显得异常，出现明显的折痕或断裂感。

网格密度与性能平衡：网格划分对动画制作至关重要，它定义了皮肤如何弯曲。然而，密集网格会导致性能开销增加。因此需要在视觉质量和性能之间找到平衡点。通常的做法是：在关节等关键变形区域使用较高密度的网格，在相对平坦的区域（如躯干、大腿）使用较低密度的网格。

骨骼绑定（Skeleton Binding）

完成网格模型后，需要为模型创建骨骼系统。骨骼是控制角色运动的基础，通过骨骼的旋转、平移和缩放来实现角色的各种动作。

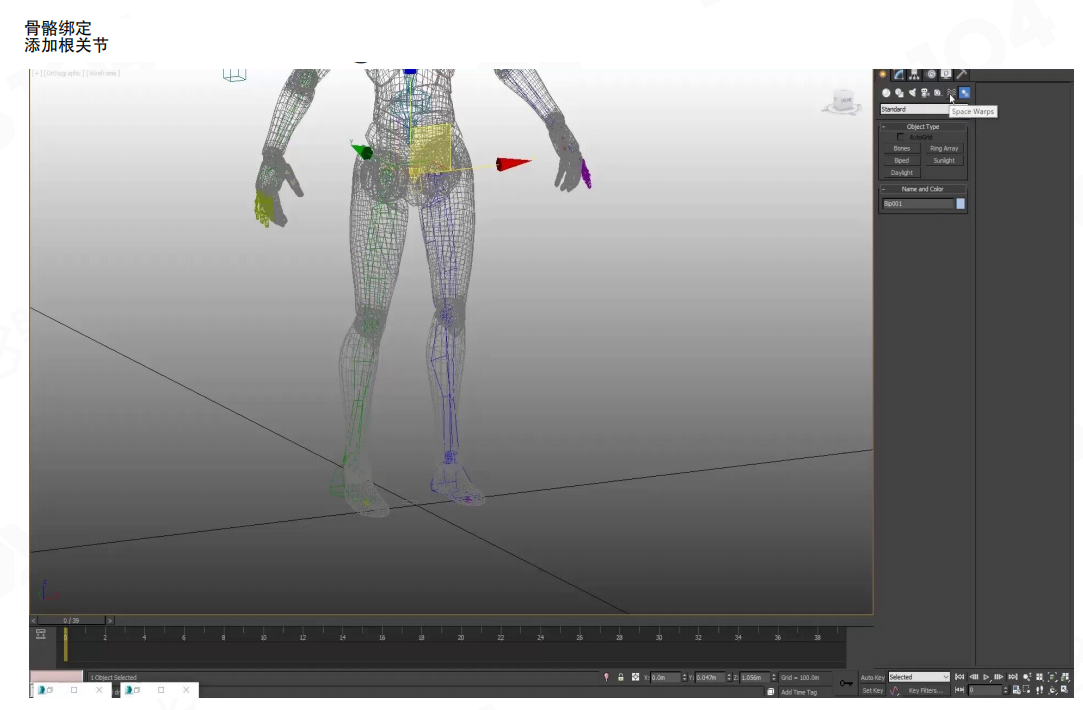
预制骨架系统：目前主流的三维建模软件（如3ds Max、Maya、Blender）都集成了骨骼功能，通常提供预制骨架（Biped）系统。这些预制骨架针对人形角色进行了优化，包含标准的骨骼结构（如脊柱、四肢、手指等），美术人员可以在此基础上进行微调。

骨骼创建流程：

添加根关节：首先创建根关节（Root Joint），通常位于角色的骨盆或两脚之间，作为整个骨骼系统的根节点。
构建骨骼层级：按照角色的身体结构，从根关节开始逐级创建子关节，形成树状的骨骼层级结构。
调整骨骼位置：将骨骼手动附加到Mesh的指定位置，确保骨骼与模型的几何结构对齐。

游戏玩法关节：在角色基本骨骼的基础上，一般还会根据游戏玩法进一步添加一些额外的关节，包括：

武器挂点（Weapon Mount Point）：用于绑定武器、道具等装备
坐骑关节（Mount Joint）：用于角色与坐骑的绑定
特效挂点（Effect Mount Point）：用于绑定粒子效果、特效等

这些附加关节使得角色能够与游戏中的各种元素进行交互，增强了游戏的表现力和可玩性。

蒙皮（Skinning）

蒙皮是将网格顶点绑定到骨骼上的过程，决定了顶点如何跟随骨骼运动。这是动画制作中最关键也最复杂的环节之一。

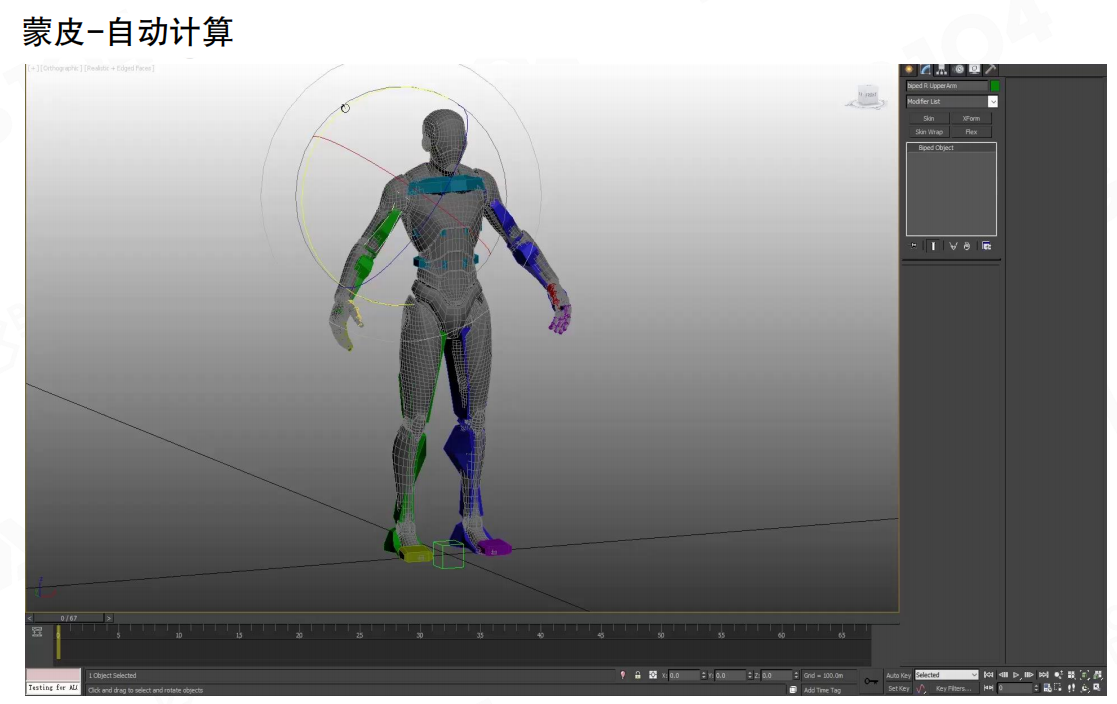
自动蒙皮计算：现代DCC软件通常提供自动蒙皮（Automatic Skinning）功能，系统会根据顶点与骨骼的距离自动计算初始的蒙皮权重。自动计算可以快速生成基础的绑定关系，但通常需要手动校正才能达到理想效果。

蒙皮权重调整：自动计算的结果往往不够精确，特别是对于复杂的几何结构或需要精细控制的区域（如面部、手部）。因此，蒙皮过程一般需要在软件自动计算的基础上，结合建模师的经验进行手动校正：

权重绘制：使用权重绘制工具，手动调整每个顶点受不同骨骼影响的权重值
关节区域优化：重点调整关节附近的权重分布，确保变形平滑自然
测试验证：通过旋转骨骼测试变形效果，反复调整直到满意

蒙皮质量要求：

平滑过渡：相邻顶点的权重应该平滑过渡，避免突变
权重归一化：每个顶点的所有权重之和应该等于1
合理影响范围：每个顶点通常受2-4个骨骼影响，过多会影响性能，过少会导致变形不自然

动画创作（Animation Creation）

完成蒙皮后，动画师就可以开始制作角色的动画了。动画创作是通过设置关键帧来定义角色在不同时间点的姿态，然后由软件自动插值生成完整的动画序列。

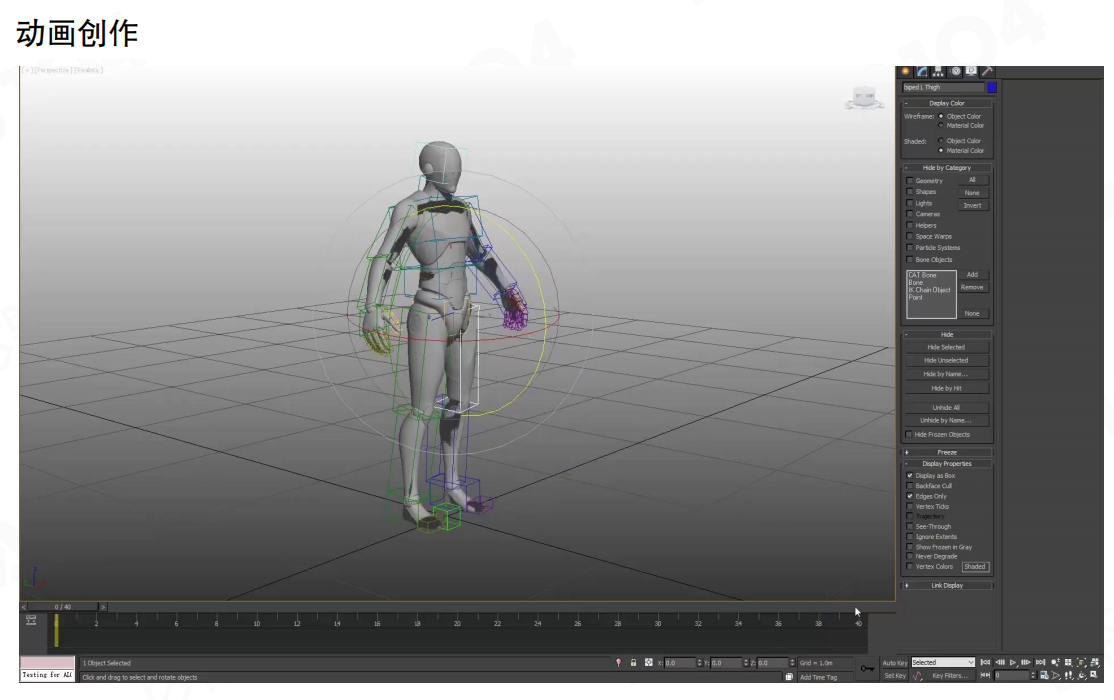
关键帧动画：动画师根据关键帧设置模型的动作。关键帧定义了动画中重要的时间点和姿态，软件会在关键帧之间自动进行插值计算，生成平滑的过渡动画。

动画制作流程：

设置初始姿态：确定动画的起始姿态（通常是绑定姿势或T-pose/A-pose）
创建关键帧：在时间轴上设置关键帧，调整骨骼姿态
调整动画曲线：通过动画曲线编辑器调整关键帧之间的插值方式，控制动画的节奏和缓动效果
预览和优化：实时预览动画效果，反复调整直到达到预期

动画类型：

基础动画：走、跑、跳等基本动作
战斗动画：攻击、防御、技能释放等战斗动作
表情动画：面部表情、眼神变化等细节动画
交互动画：开门、拾取物品等环境交互动作

导出（Exporting）

在DCC软件中完成动画资源制作后，需要将资源导出到游戏引擎中使用。导出过程看似简单，但实际上涉及许多技术细节，需要确保数据的一致性和完整性。

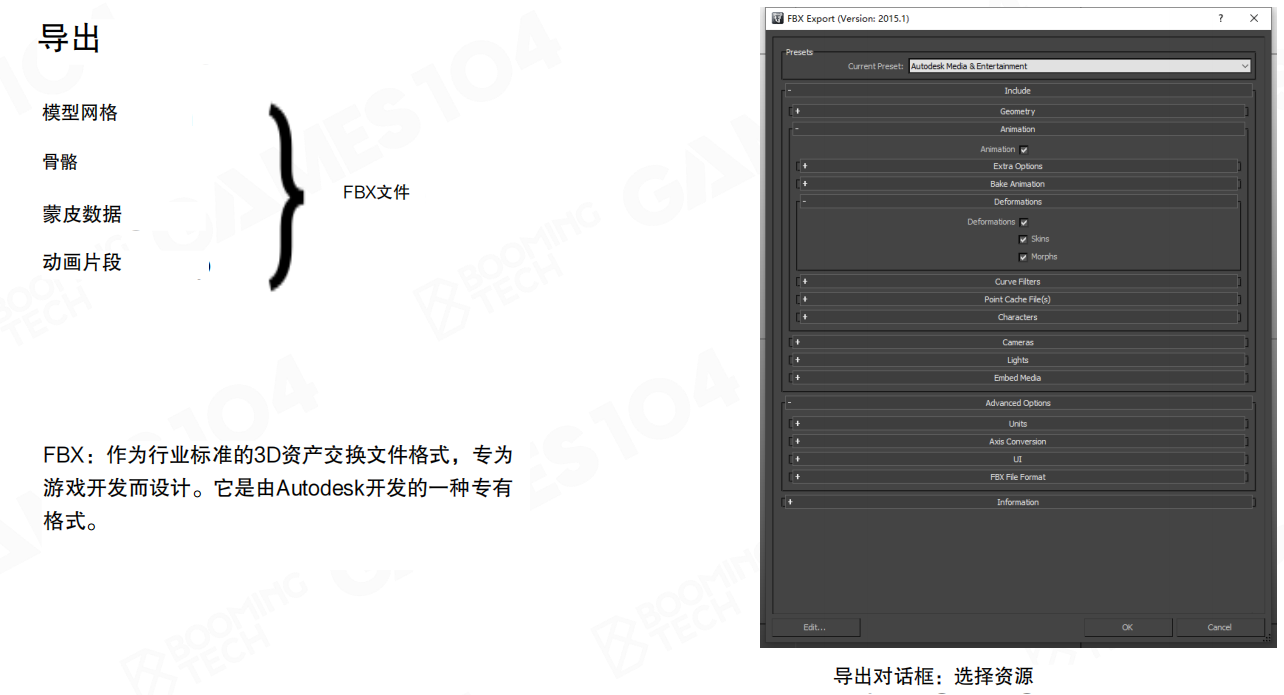
FBX格式：目前工业标准是使用FBX格式来保存动画所需的全部几何运动数据。FBX（Filmbox）是由Autodesk开发的一种专有格式，作为行业标准的3D资产交换文件格式，专为游戏开发而设计。

FBX文件包含的内容：

模型网格（Model Mesh）：角色的几何数据
骨骼（Skeleton）：骨骼层级结构和绑定信息
蒙皮数据（Skin Data）：顶点权重和骨骼绑定关系
动画片段（Animation Clips）：关键帧数据和动画曲线

导出注意事项：

尺寸单位一致性：确保DCC软件和游戏引擎使用相同的单位系统（通常是米或厘米）。单位不一致会导致模型尺寸错误，影响物理模拟和碰撞检测。
坐标系一致性：不同软件可能使用不同的坐标系（左手系/右手系、Y-up/Z-up等）。导出时需要正确设置坐标系转换，确保模型在引擎中的朝向正确。
是否附带位移曲线：根骨骼的位移信息（Root Motion）对于游戏中的角色移动非常重要。需要明确是否导出根骨骼的位移曲线，以便在引擎中实现基于动画的角色移动。
动画帧率设置：确保导出的动画帧率与游戏引擎的帧率设置一致，避免动画播放速度异常。
骨骼命名规范：使用统一的骨骼命名规范，便于在引擎中进行骨骼查找和动画重定向。
材质和纹理：虽然FBX可以包含材质信息，但通常建议单独导出纹理文件，在引擎中重新设置材质，以获得更好的控制和优化。

导出对话框配置：在FBX导出对话框中，需要仔细选择导出的资源类型：

几何体（Geometry）：包含网格数据
动画（Animation）：包含动画关键帧数据
变形（Deformations）：包含蒙皮和形变数据
烘焙动画（Bake Animation）：将动画烘焙到每一帧，提高兼容性但增加文件大小

动画制作流程总结

完整的动画DCC流程是一个从模型到动画的完整制作链条，每个环节都至关重要：

网格构建：创建适合动画的低精度模型，在关节处加密网格
骨骼绑定：建立骨骼系统，添加游戏玩法相关的附加关节
蒙皮：将顶点绑定到骨骼，调整权重确保变形自然
动画创作：通过关键帧制作各种动画动作
导出：将完整的动画资源导出为FBX格式，供游戏引擎使用

这个流程需要建模师、绑定师、动画师等多个专业人员的协作，每个环节的质量都直接影响最终的游戏表现。现代游戏引擎通常提供完善的导入和优化工具，能够自动处理大部分技术细节，让美术人员能够专注于创作本身。

转载请注明来源，欢迎对文章中的引用来源进行考证，欢迎指出任何有错误或不够清晰的表达。可以在下面评论区评论，也可以邮件至 785293209@qq.com