10.游戏引擎中物理系统的基础理论和算法

游戏引擎 > 引擎体系 > 现代游戏引擎入门游戏引擎引擎体系现代游戏引擎入门

发布时间 : 2025-12-02 12:25

字数:16.8k 阅读 :

评论:

10.游戏引擎中物理系统的基础理论和算法

10.游戏引擎中物理系统的基础理论和算法

10.1 物理系统

物理系统是游戏引擎的重要组成部分。在游戏中，玩家和整个游戏世界的互动都依赖于物理系统的实现。同时，现代游戏中大量的粒子效果也都是通过物理系统来驱动的。显然物理系统非常复杂，甚至有很多公司专门研究物理引擎的高效实现。

物理系统的解算比渲染和动画更复杂。如果说渲染是在画布上绘制画面，动画是在时间轴上播放动作，那么物理系统就是在模拟整个世界的运行规律——物体如何运动、如何碰撞、如何受力，这些都需要精确的数学计算。

物理系统的核心组成

物理系统主要包含以下几个核心部分：

基本概念：物理角色与形状、部队等基础对象。就像搭建积木，先要有基本的积木块，才能组合成复杂的结构。

力与运动：描述物体在空间中的位置变化。物体如何移动、旋转，速度如何变化，这些都是运动系统要解决的问题。

刚体动力学：处理刚体（不会变形的物体）的运动和受力。比如一个箱子被推倒，它会如何翻滚、如何停止，这些都需要刚体动力学来计算。

碰撞检测：判断两个物体是否发生碰撞。就像两个球相撞，需要先知道它们是否碰到了一起。

碰撞解析：处理碰撞发生后的反应。两个物体碰撞后，它们应该如何分离、如何反弹，这需要碰撞解析来计算。

场景查询：在场景中查找满足条件的物体。比如查找某个区域内的所有物体，或者查找距离某个点最近的物体。

效率、准确性与确定性：物理系统需要在计算速度、计算精度和结果一致性之间找到平衡。游戏需要在每帧30ms内完成所有物理计算，同时还要保证结果准确，并且在多人游戏中保证所有玩家看到的结果一致。

物理系统的应用

物理系统在游戏中有广泛的应用：

角色控制器：控制角色在地面上的移动、跳跃、攀爬等行为。角色如何与地面交互，如何避免穿墙，这些都是角色控制器要解决的问题。

布娃娃系统：角色受击或死亡时的物理模拟。就像提线木偶，角色失去控制后，身体会按照物理规律自然下落和摆动。

破坏系统：物体被破坏时的物理效果。一堵墙被炸毁，碎片如何飞散，如何落地，这些都需要物理系统来模拟。

布料模拟：衣服、旗帜等柔性物体的运动。布料如何随风飘动，如何与角色身体贴合，这些都是布料模拟的范畴。

载具系统：车辆、飞机等载具的物理行为。车辆如何加速、转向、刹车，如何与地面交互，这些都是载具系统要处理的问题。

高级物理：基于位置的动力学（PBD）等更先进的物理仿真技术，能够实现更真实、更稳定的物理效果。

物理系统是游戏真实感的重要来源。一个优秀的物理系统能让玩家感觉游戏世界是”活的”，物体有重量、有惯性，碰撞有反馈，一切都符合我们对现实世界的认知。

10.2 物理对象与形状

在游戏引擎中，我们看到的画面和物理系统处理的对象是完全不同的两套东西。玩家看到的是精美的渲染画面，而物理系统处理的则是简化的几何形状。就像一座房子，外观可以很复杂，但结构工程师只需要知道它的基本框架就够了。再比如说人物，一般可能只是个胶囊体。

物理对象（Actor）

在物理引擎中，我们把参与物理模拟的对象称为Actor（演员）。根据对象的特点，可以把它们分为几种类型。

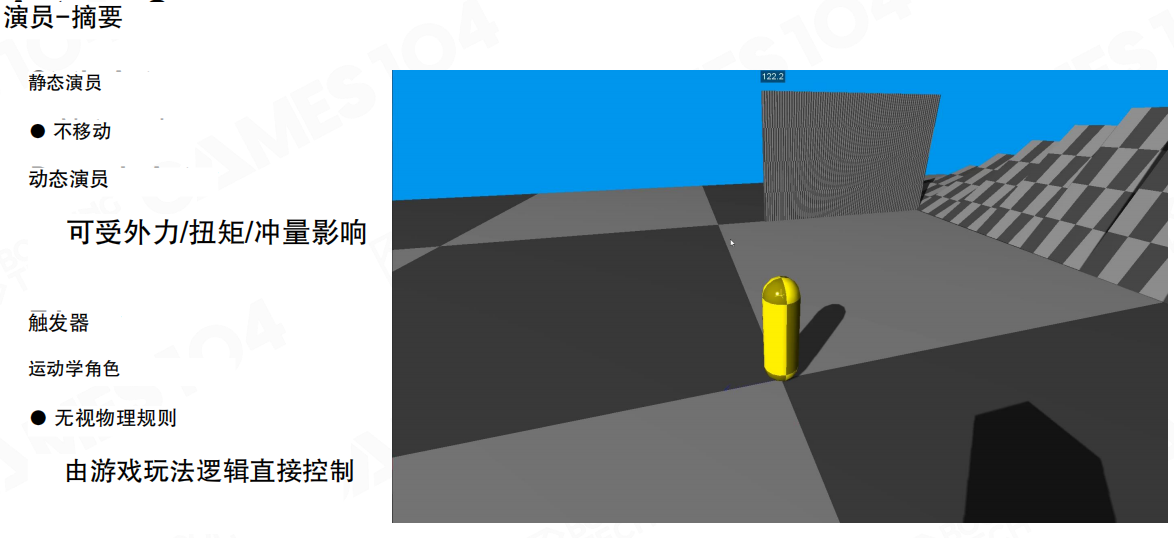
静态对象（Static Actor）

静态对象在仿真过程中不会发生改变，它们有碰撞，但不会动。比如游戏中的地面、墙壁、建筑物等。这些对象就像舞台上的背景道具，永远固定在原地。

动态对象（Dynamic Actor）

动态对象会受到外力、扭矩或冲量的影响，它们的运动状态会在游戏过程中动态变化，而且运动过程需要符合相应的动力学模型。比如一个箱子被推倒，它会按照物理规律翻滚、停止。

触发器（Trigger）

触发器类似于静态对象，不移动，但它不阻塞其他对象。当角色进入或退出触发器区域时，会发出通知，用来触发相关逻辑。比如角色走进一个区域，触发开门、播放音效等。

运动学角色（Kinematic Character）

运动学角色无视物理规则，由游戏玩法逻辑直接控制。它不完全基于物理法则，但往往与玩法高度相关。比如角色控制器，它按照玩家的输入移动，而不是按照物理力移动。

需要注意的是，如果在一个游戏世界中部分基于物理，部分不基于物理，可能会产生一些反常的效果，处理起来比较麻烦。就像在一个真实的物理世界中，突然出现一个不受重力影响的物体，会显得很突兀。

物理形状（Shape）

物理对象最重要的属性是它的形状。复杂几何体之间的求交非常复杂，因此物理系统中会用形态简单、可以快速求解的几何体来近似复杂的模型。就像用简单的积木块来代表复杂的物体，虽然不够精确，但计算起来快得多。

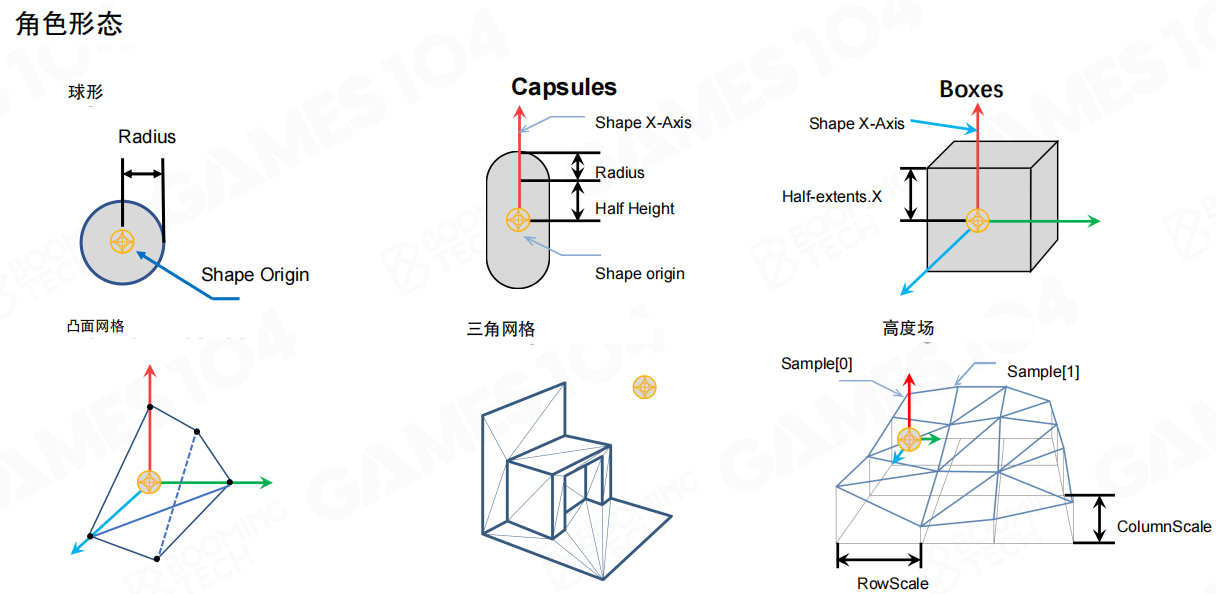
球形（Sphere）

球形是最简单的碰撞形状，只需要一个半径参数。球形在物理计算中非常高效，常用于球类游戏，比如台球、网球、足球、排球等。这些游戏中的球都是完美的球形，碰撞检测和响应都很简单。

胶囊体（Capsule）

胶囊体由一个圆柱体和两个半球体组成，需要半径和半高两个参数。胶囊体非常适合用来表示角色，因为它能很好地近似站立的人形，而且滚动时很平滑。在游戏中，每个角色通常都被一个胶囊体包围，用于碰撞检测。

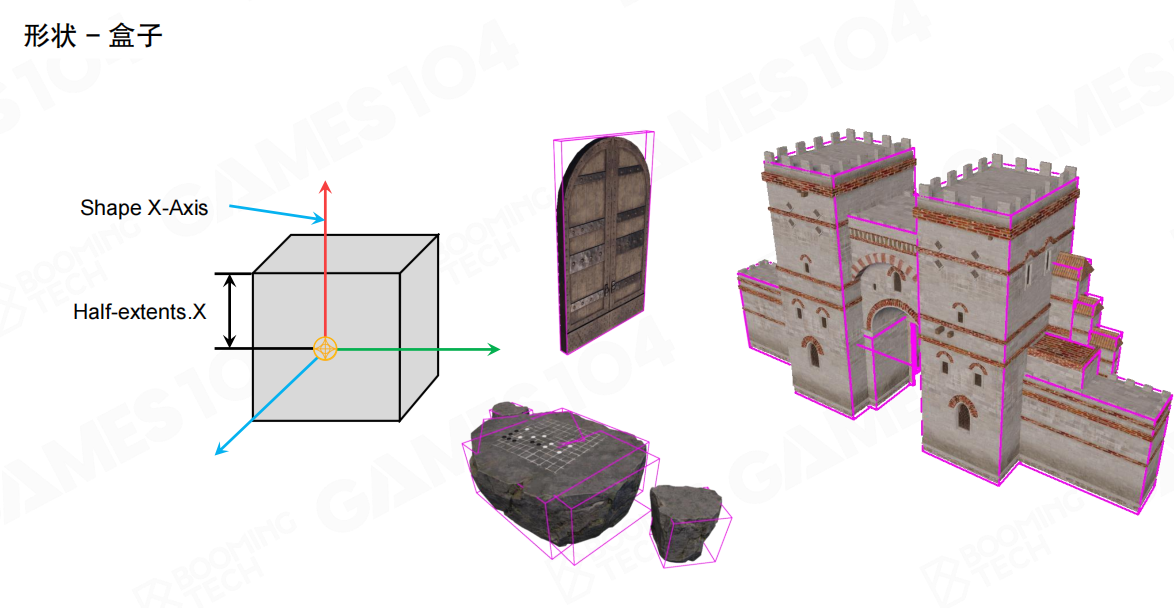
盒子（Box）

盒子是一个长方体，需要三个半轴长度参数。盒子是最常用的碰撞形状之一，可以用来表示各种规则物体，比如门、箱子、建筑物等。即使是很复杂的模型，也可以用多个盒子来近似。

凸面网格（Convex Mesh）

凸面网格是一个凸多面体，可以表示比基本形状更复杂的形状，同时保持计算效率。凸面网格有顶点和面数的限制，不能太复杂。它适合表示一些不规则但仍然是凸形的物体。

三角网格（Triangle Mesh）

三角网格可以表示任意复杂的形状，包括凹形。但动态角色无法使用三角网格，因为三角网格的计算成本太高。三角网格主要用于静态环境，比如复杂的地形、建筑物等。

高度场（Heightfield）

高度场专门用于表示地形，通过网格采样来定义高度变化。高度场非常适合大规模地形的碰撞检测，计算效率很高。比如游戏中的山地、平原等地形，都可以用高度场来表示。

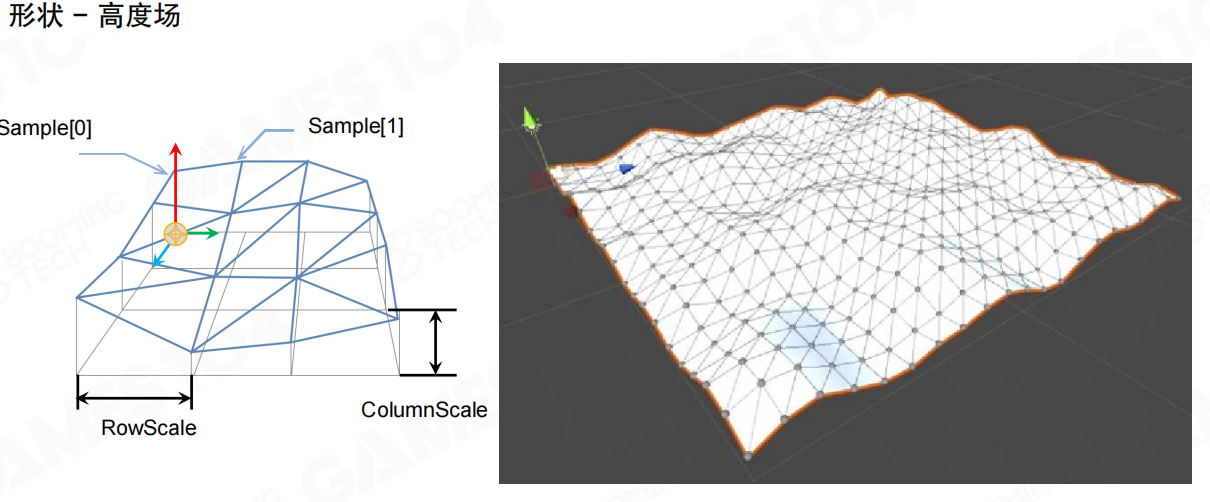
形状使用原则

在进行物理仿真时，我们首先会把物理对象进行一定的包裹，使用相对简单的几何形状来近似复杂的模型。这里有几个重要原则：

近似环绕：无需追求完美，只要近似即可。就像用纸箱装东西，不需要完全贴合，只要能装下就行。

简洁性：优先选择简单形状，如有可能，尽量避免使用三角网格。简单形状计算快，复杂形状计算慢。

最简形状：能用球形就不用胶囊体，能用盒子就不用网格。越简单的形状，计算效率越高。

形状属性

在形状的基础上，我们还需要对一些物理量进行定义，包括对象的质量或密度、质心以及物理材质等。

质量与密度

质量决定了物体受力的响应程度。质量越大，越难推动。密度是单位体积的质量，一个物体内的密度通常是均匀分布的。比如一个冈布茨形状，它的质量分布会影响它的稳定性。

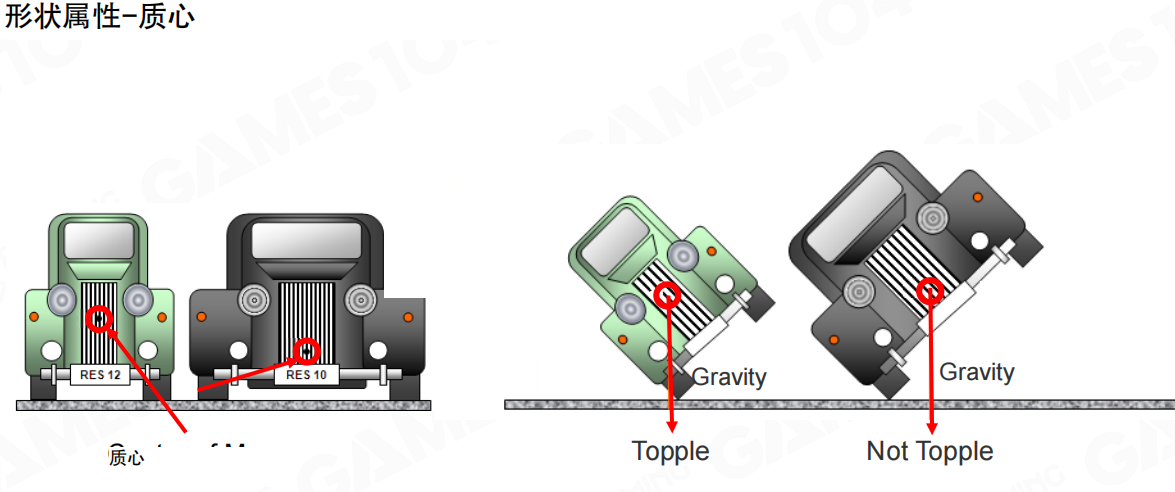
质心（Center of Mass）

质心是物体质量的中心点，它决定了物体的稳定性。质心越低，物体越稳定，越不容易翻倒。比如一辆车的质心如果很高，转弯时容易翻车；如果质心很低，即使倾斜也不会翻倒。

摩擦力与弹性（Friction & Restitution）

摩擦力决定了物体在表面上的滑动阻力。摩擦力越大，物体越难滑动。弹性（回弹系数）决定了物体碰撞后的能量损失。弹性越大，物体碰撞后反弹得越高；弹性越小，物体碰撞后能量损失越多，反弹越低。

这些属性共同决定了物体在物理世界中的行为。一个物体的形状、质量、质心、摩擦力和弹性，都会影响它在碰撞、运动、受力时的表现。物理系统就是通过这些简化的形状和属性，来模拟复杂的物理世界。

10.3 力与运动

物理系统要模拟物体的运动，首先要理解力和运动的关系。在游戏中，我们通过施加力来改变物体的运动状态，就像推一个箱子，箱子会加速移动一样。

力与冲量

力（Force）是改变物体运动状态的原因。我们可以施加力来赋予动态物体加速度，从而影响其运动状态。在物理引擎中，常见的力包括：

重力：物体受到的地球引力，让物体自然下落
拖拽力（Drag）：物体在流体中运动时受到的阻力，比如空气阻力
摩擦力：物体接触时产生的阻力，影响物体的滑动和滚动

这些力持续作用在物体上，会逐渐改变物体的速度。就像推一个箱子，持续用力，箱子会越推越快。

冲量（Impulse）是另一种常用的仿真方式。我们可以通过施加冲量来立即改变角色的速度。冲量比较适合用来模拟物体运动状态发生剧烈变化的情况，比如模拟一场爆炸。当爆炸发生时，附近的物体会瞬间受到巨大的冲击，速度发生剧烈变化。使用冲量可以更直接地模拟这种瞬间的变化，而不需要计算持续作用的力。

牛顿运动定律

要理解力如何影响运动，我们需要回到基础的物理定律。

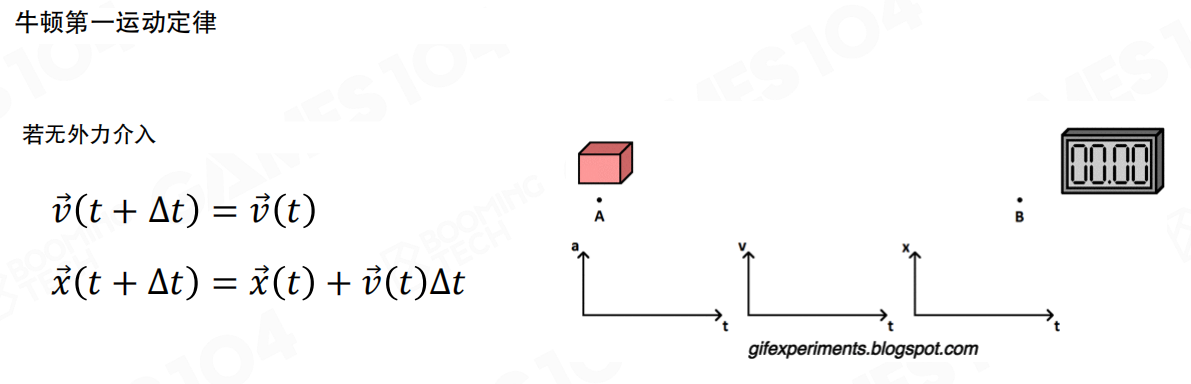
牛顿第一运动定律（惯性定律）：若无外力介入，物体具有惯性，会保持原有状态。也就是说，如果物体不受力，它会保持匀速直线运动或静止。用数学公式表示：

速度不变：v(t + Δt) = v(t)
位置更新：x(t + Δt) = x(t) + v(t)Δt

这就像在太空中，没有空气阻力，一个物体一旦开始运动，就会一直运动下去。

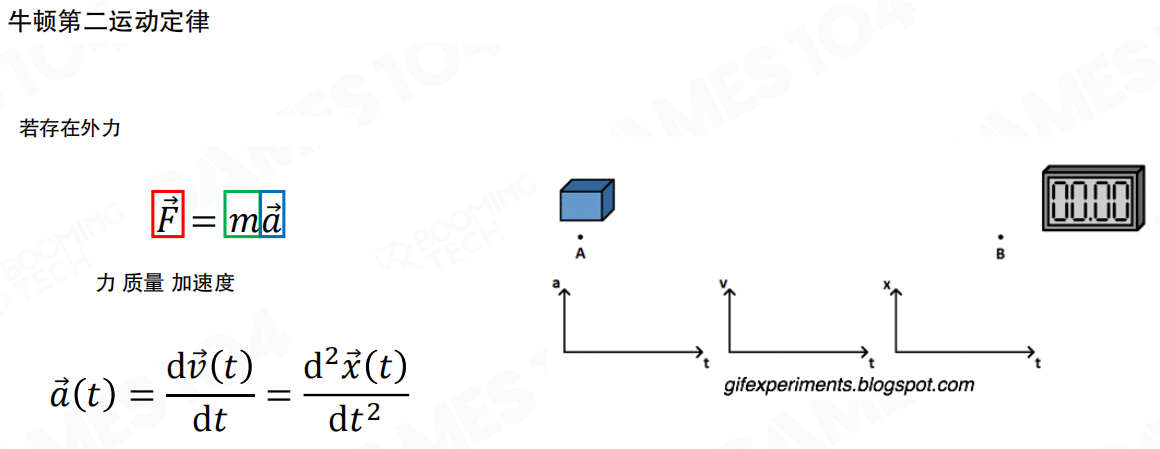
牛顿第二运动定律：若存在外力，力等于质量乘以加速度。这就是著名的公式：

F = ma

其中：

F 是力（向量）
m 是质量
a 是加速度（向量）

加速度是速度的变化率，也是位置的二阶导数：

a(t) = dv(t)/dt = d²x(t)/dt²

这个定律告诉我们，力越大，加速度越大；质量越大，同样的力产生的加速度越小。就像推一个空箱子和推一个装满书的箱子，同样的力，空箱子更容易推动。

恒定力作用下的运动

当力是恒定的时候，我们可以直接推导出速度和位置的更新公式。

从牛顿第二定律 F = ma，我们可以得到加速度：

a = F / m

然后，在时间步长 Δt 内，速度和位置的更新公式为：

速度更新：v(t + Δt) = v(t) + a(t)Δt
位置更新：x(t + Δt) = x(t) + v(t)Δt + (1/2)a(t)Δt²

这就是恒定力作用下的运动公式。比如一个物体在重力作用下下落，重力是恒定的，我们可以用这个公式计算每一帧的位置。

变力作用下的运动

但在实际游戏中，力往往是变化的。比如一个弹簧，随着压缩程度不同，力的大小也不同。

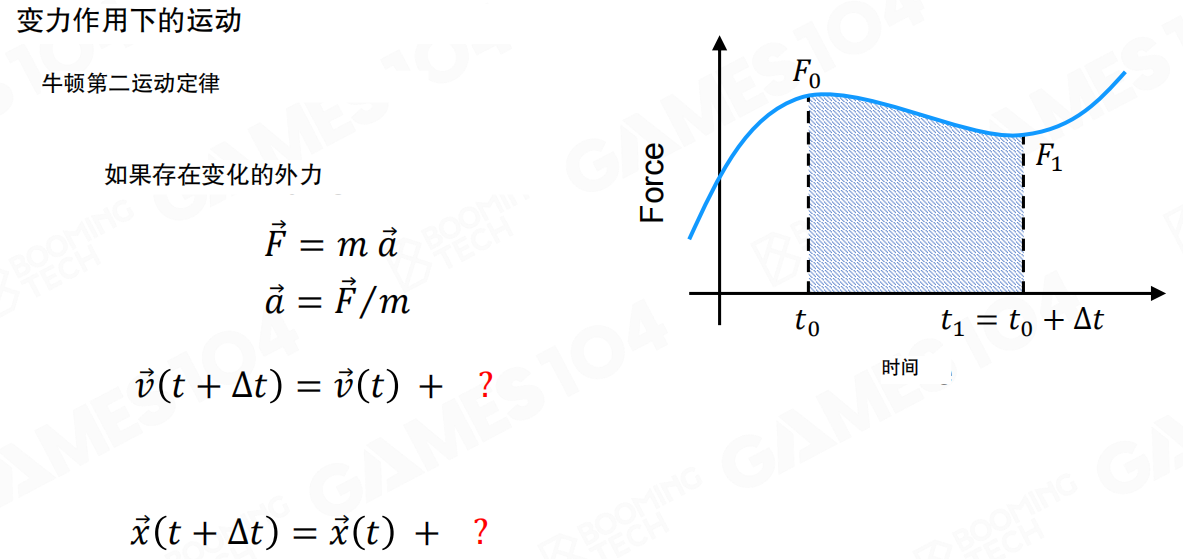
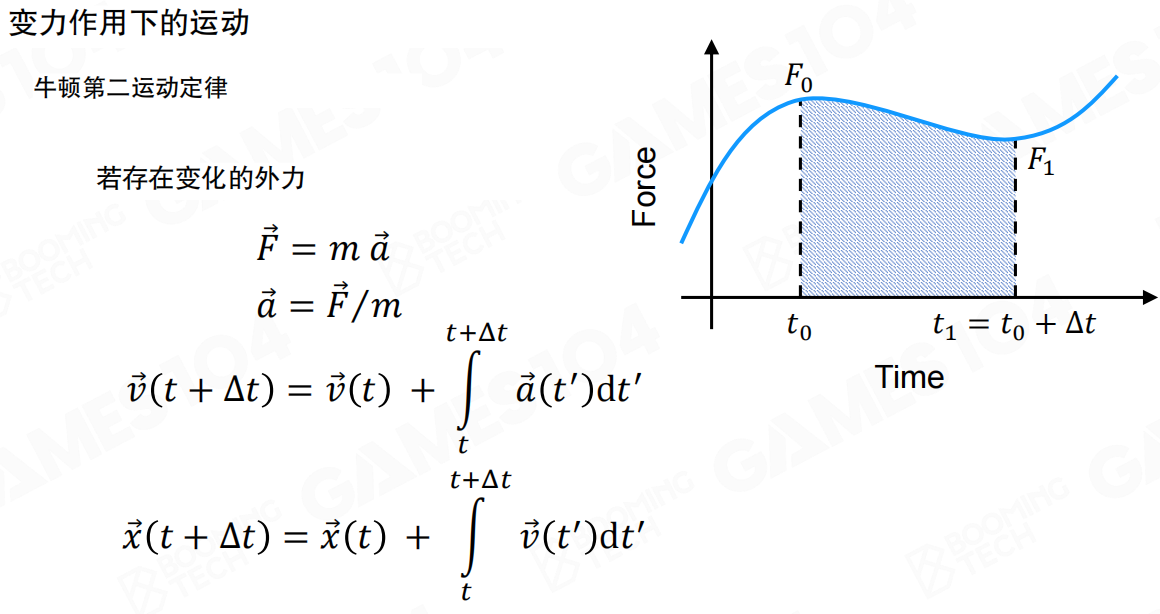
当力随时间变化时，我们需要使用积分来计算速度和位置的变化：

速度更新：v(t + Δt) = v(t) + ∫[t到t+Δt] a(t')dt'
位置更新：x(t + Δt) = x(t) + ∫[t到t+Δt] v(t')dt'

这里的积分表示在时间间隔 Δt 内，加速度和速度的累积效果。就像计算一个变力做的功，需要把每一小段时间内的力乘以位移，然后累加起来。

运动状态的描述

在描述物体的运动时，我们需要知道几个关键量。

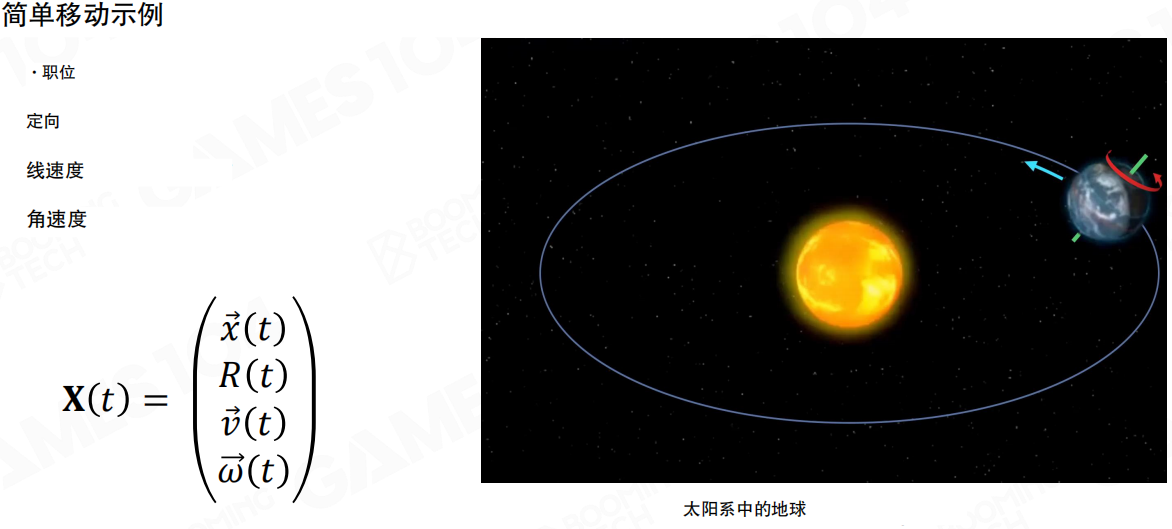
物体的完整运动状态可以用一个状态向量 X(t) 来描述：

X(t) = [
  x(t)    // 位置（向量）
  R(t)    // 方向（旋转矩阵）
  v(t)    // 线速度（向量）
  ω(t)    // 角速度（向量）
]

比如地球在太阳系中的运动，既有围绕太阳的公转（线速度），也有自身的自转（角速度）。位置告诉我们地球在哪里，方向告诉我们地球的朝向，线速度告诉我们地球移动得多快，角速度告诉我们地球转得多快。

在现实中的运动，我们需要知道：

位置 x(t)：物体在空间中的位置（向量）
线速度 v(t) = dx(t)/dt：位置对时间的导数，表示物体移动的速度（向量）

在游戏中的模拟，我们的目标是：

给定当前时刻 t 的位置 x(t) 和速度 v(t)（都是向量）
计算下一时刻 t + Δt 的位置 x(t + Δt) 和速度 v(t + Δt)（都是向量）

其中 Δt 是时间步长，通常是每帧的时间间隔（比如 1/60 秒）。

数值积分方法

在物理引擎中，我们一般无法使用解析的方式来计算物体的运动，因为力往往是复杂的函数。因此我们需要一些数值计算方法来进行求解。

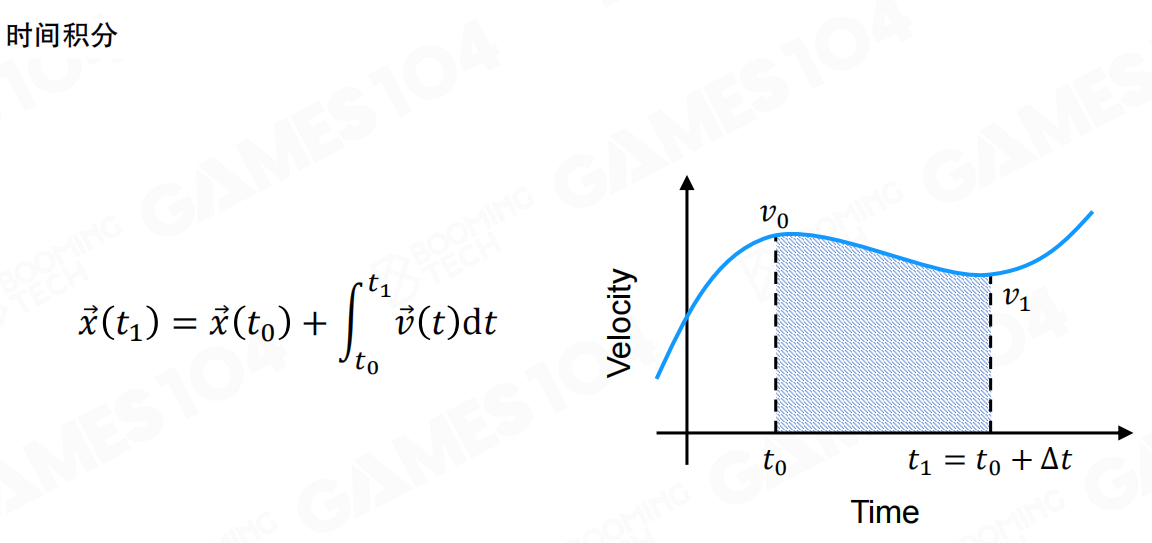
数值积分的核心思想是：我们可以把时间间隔设置成一个比较小的值，然后对被积函数进行累加来近似实际的积分。位置的变化可以通过速度的积分来计算：

x(t₁) = x(t₀) + ∫[t₀到t₁] v(t) dt

这个积分表示从 t₀ 到 t₁ 这段时间内，速度的累积效果，也就是位置的改变量。在图像上，这个积分就是速度曲线下的面积。

数值积分的方法有很多，其中最基础、最常用的是欧拉法（Euler’s method），由数学家莱昂哈德·欧拉在18世纪提出。欧拉法非常简单，但它的稳定性问题也引出了后续的改进方法。

显式欧拉法

显式欧拉法（Explicit Euler Method），也称为前向欧拉法，是最简单的数值积分方法。

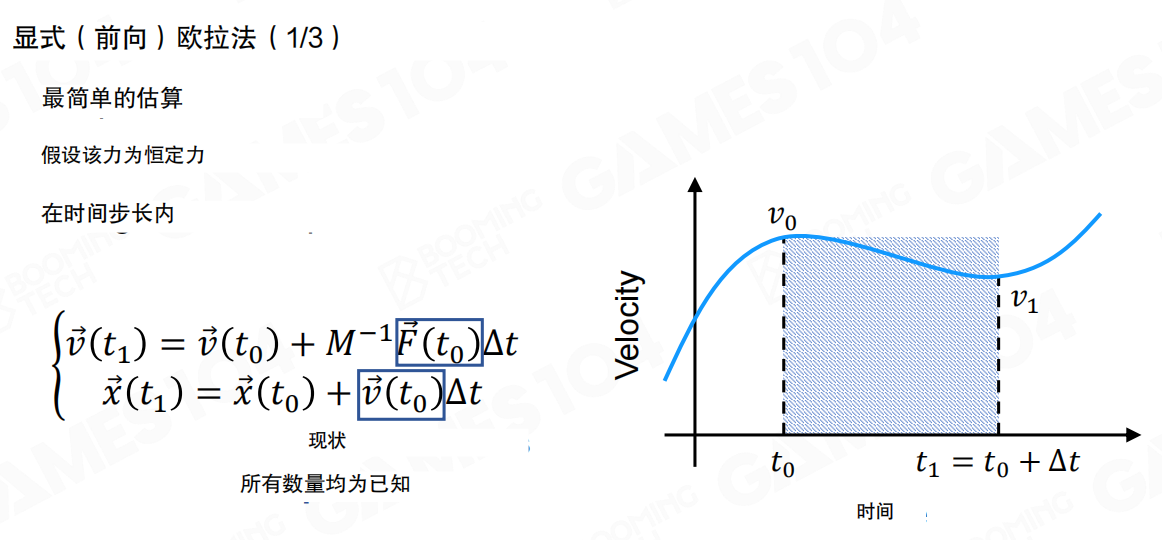
显式欧拉法的基本思想是：假设在时间步长内，力是恒定的，使用当前时刻的状态来估计下一时刻的状态。

更新公式为：

速度更新：v(t₁) = v(t₀) + M⁻¹F(t₀)Δt（使用当前时刻的力 F(t₀)）
位置更新：x(t₁) = x(t₀) + v(t₀)Δt（使用当前时刻的速度 v(t₀)）

这种方法实现起来非常简单，效率也很高。但问题在于，它使用当前时刻的状态来估计未来，本质上是”向前看”的方法，这会导致误差累积。

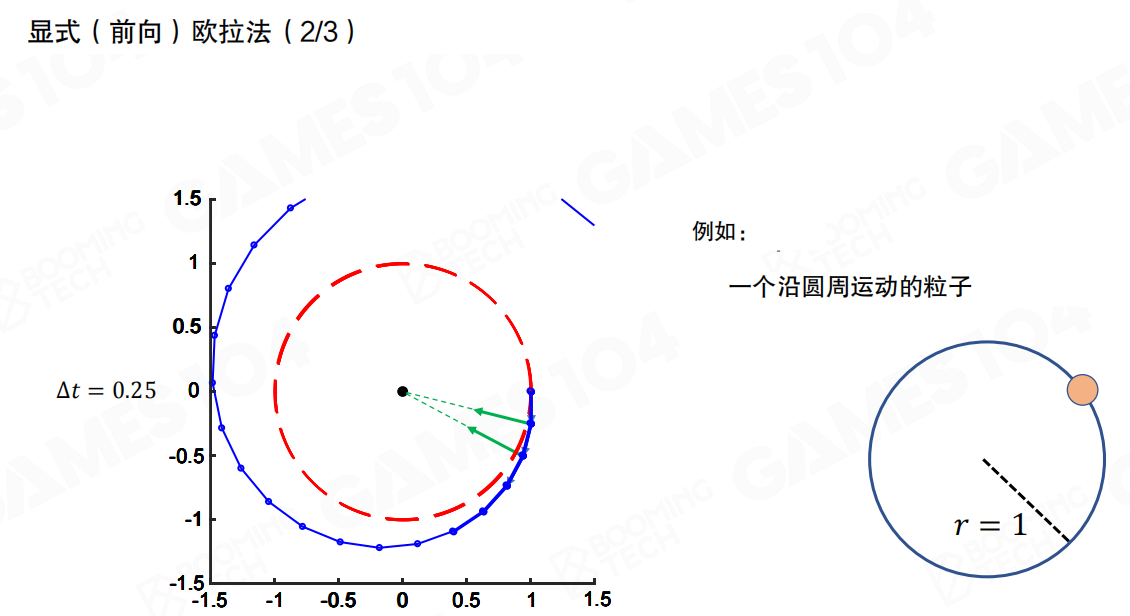
当我们用显式欧拉法模拟一个沿圆周运动的粒子时，会发现一个问题：即使时间步长很小（比如 Δt = 0.25），粒子的轨迹也会逐渐偏离圆形轨道，形成螺旋状向外发散。这是因为每一步的误差都在累积，导致能量不断增加。

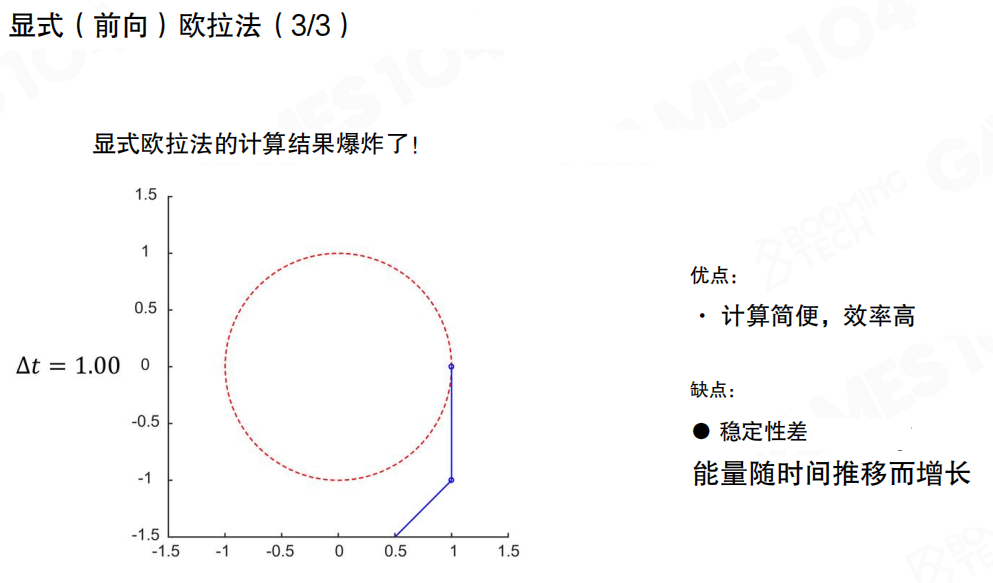
当时间步长更大时（比如 Δt = 1.00），问题会更加严重。显式欧拉法的计算结果会”爆炸”——粒子的轨迹会快速偏离真实轨道，能量随时间推移而增长，完全不符合物理规律。

显式欧拉法的特点：

优点：计算简便，效率高
缺点：稳定性差，能量随时间推移而增长

这就是为什么显式欧拉法虽然简单，但在实际游戏中很少直接使用的原因。

隐式欧拉法

为了解决显式欧拉法的稳定性问题，人们开发出了隐式欧拉法（Implicit Euler Method），也称为后向欧拉法。

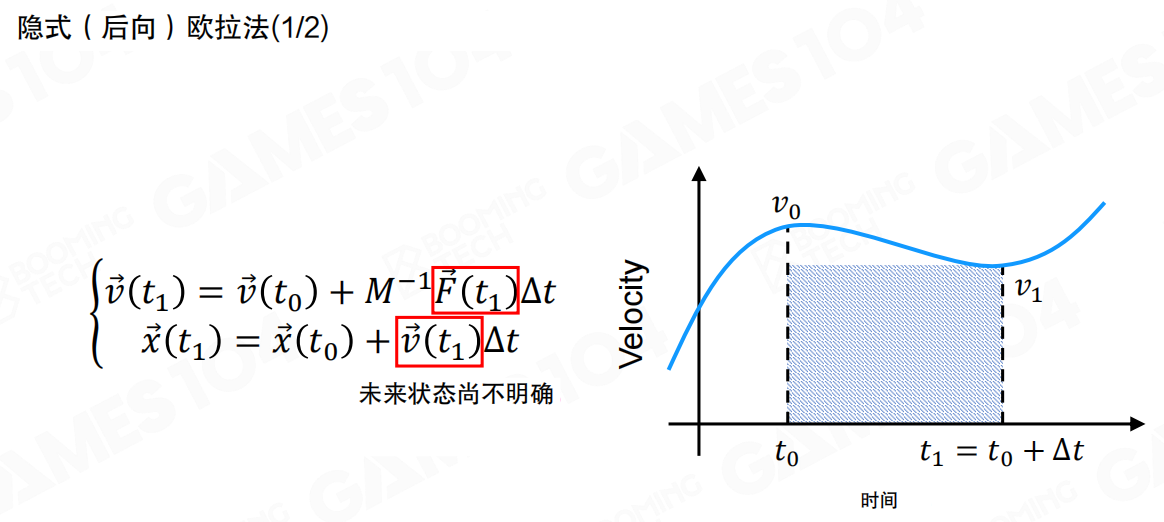
隐式欧拉法的基本思想是：使用下一时刻的状态来计算当前时刻到下一时刻的变化。

更新公式为：

速度更新：v(t₁) = v(t₀) + M⁻¹F(t₁)Δt（使用未来时刻的力 F(t₁)）
位置更新：x(t₁) = x(t₀) + v(t₁)Δt（使用未来时刻的速度 v(t₁)）

但这里有个问题：未来状态尚不明确。我们需要知道 F(t₁) 和 v(t₁) 才能计算，但这些值正是我们要计算的。这就形成了一个隐式方程，需要迭代求解。

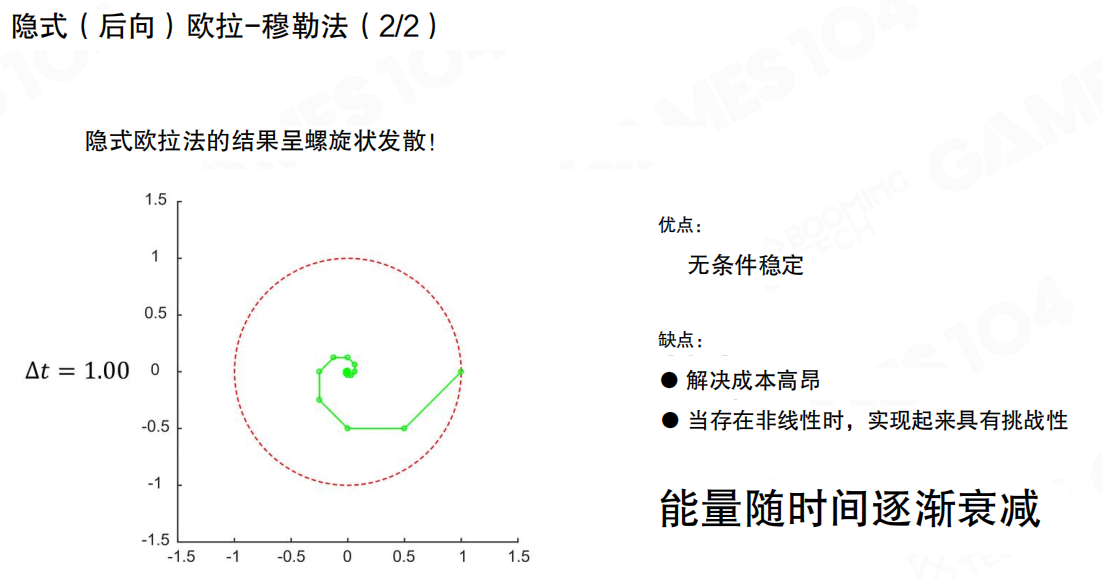
隐式欧拉法虽然解决了发散问题，但引入了新的问题：结果会呈螺旋状向内收敛。能量会随时间逐渐衰减，虽然不会爆炸，但也不符合能量守恒。

隐式欧拉法的特点：

优点：无条件稳定
缺点：解决成本高昂，当存在非线性时，实现起来具有挑战性；能量随时间逐渐衰减

由于需要求解隐式方程，计算成本很高，而且在非线性系统中实现起来很困难。所以虽然隐式欧拉法稳定，但在游戏引擎中也不常用。

半隐式欧拉法

在游戏引擎中，更常用的积分方法是半隐式欧拉法（Semi-implicit Euler Method）。

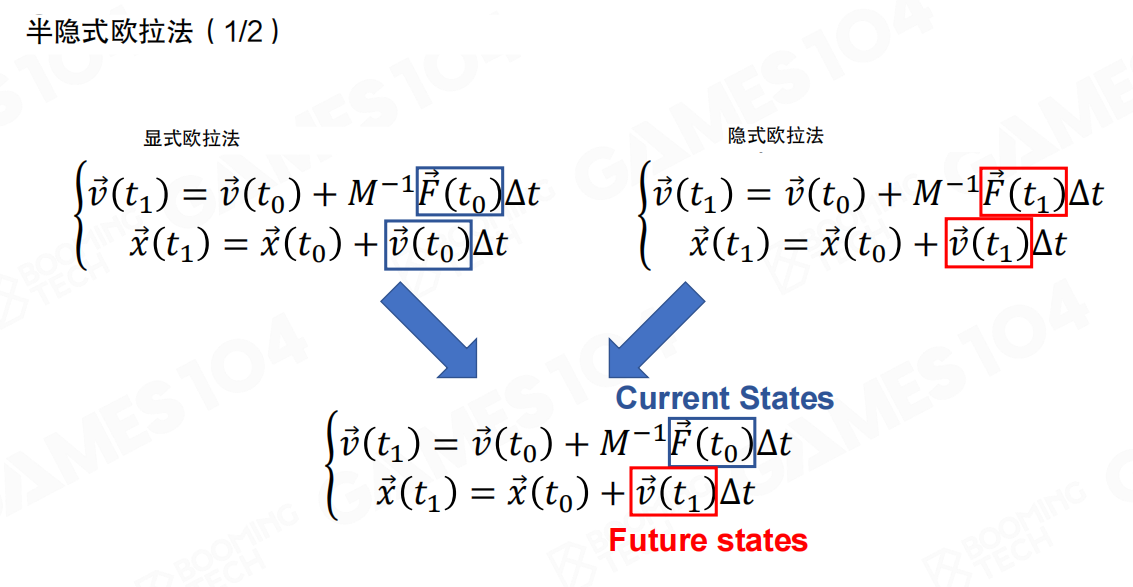
半隐式欧拉法结合了显式和隐式欧拉法的优点：

速度更新：v(t₁) = v(t₀) + M⁻¹F(t₀)Δt（使用当前时刻的力 F(t₀)，显式）
位置更新：x(t₁) = x(t₀) + v(t₁)Δt（使用刚才计算出的速度 v(t₁)，隐式）

也就是说，在计算加速度时使用当前时刻的力推导下一时刻的速度，而在计算位置时使用刚才计算出的速度再更新位置。这样既保持了计算的简单性，又提高了数值稳定性。

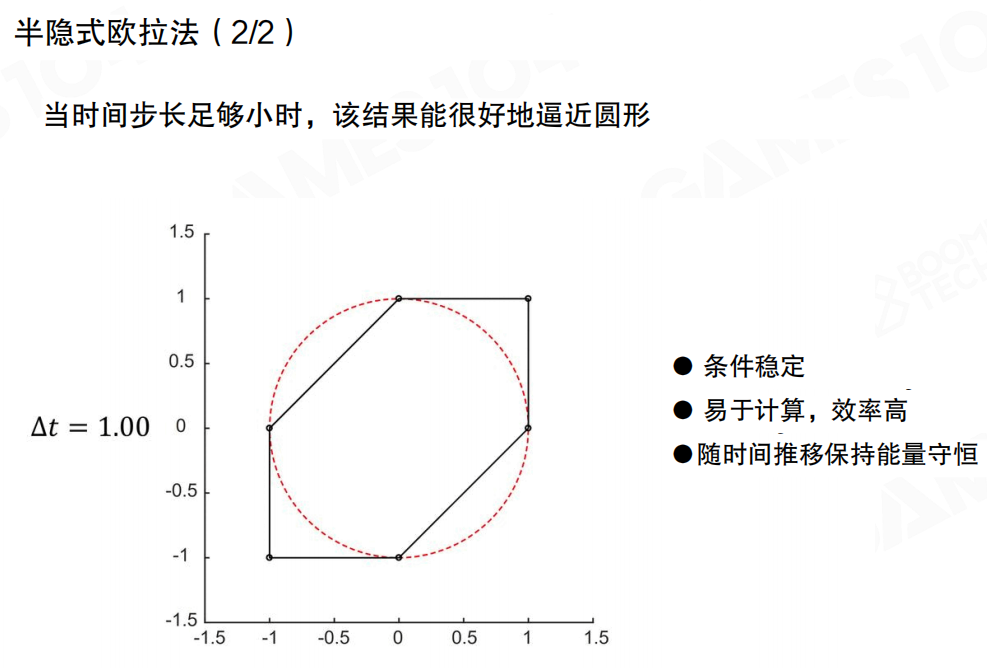
当时间步长足够小时，半隐式欧拉法的结果能很好地逼近圆形轨道。即使时间步长较大（比如 Δt = 1.00），结果也能保持稳定，形成一个近似的多边形（比如六边形），而不会发散或过度衰减。

半隐式欧拉法的特点：

条件稳定：在合理的时间步长下保持稳定
易于计算，效率高：不需要求解隐式方程，计算简单
随时间推移保持能量守恒：能量不会无限增长，也不会过度衰减

半隐式方法有非常高的数值稳定性，广泛应用于各种类型的物理仿真中。这就是为什么现代游戏引擎（如Unity的PhysX、Unreal的Chaos）都采用半隐式欧拉法作为默认的积分方法。

总结

力与运动是物理系统的基础。通过施加力或冲量，我们可以改变物体的运动状态。但要准确模拟物体的运动，我们需要：

理解牛顿运动定律：力如何产生加速度，加速度如何改变速度和位置
选择合适的数值积分方法：在计算效率、稳定性和准确性之间找到平衡
使用半隐式欧拉法：这是游戏引擎中最常用的方法，既简单又稳定

物理系统的运动模拟是一个复杂的数值计算问题。不同的积分方法有不同的特点，选择合适的方法对保证物理仿真的准确性和稳定性至关重要。

10.4 刚体动力学

前面我们讨论了力与运动，但那些都是基于质点动力学的。在质点动力学中，所有物体都被抽象为没有具体形状的质点，我们只需要按照牛顿定律更新质点的运动状态即可。但在实际游戏中，物体是有形状的，会旋转的。比如一个箱子被推倒时会翻滚，一个球被击打时会旋转。这就需要刚体动力学来处理。

从质点动力学到刚体动力学

质点动力学（Particle Dynamics）是最简单的物理仿真情况。在质点动力学中，我们只需要关注物体的位置、速度、加速度、质量和力：

位置 x(t)：物体在空间中的位置（向量）
线速度 v = dx/dt：位置对时间的导数（向量）
加速度 a = dv/dt = d²x/dt²：速度对时间的导数（向量）
质量 M：物体的质量（标量）
动量 p = Mv：质量乘以速度（向量）
力 F = dp/dt = Ma：动量的变化率，等于质量乘以加速度（向量）

质点动力学就像把物体看作一个点，只关心它在哪里、移动得多快，不关心它的形状和旋转。这在某些情况下是足够的，比如模拟一个很小的粒子，或者物体的大小可以忽略不计。

但在游戏引擎中，更为常见的仿真场景是刚体动力学（Rigid Body Dynamics）。和质点动力学不同，刚体动力学仿真需要考虑物体自身的形状，也因此需要在质点运动的基础上引入刚体旋转的相关概念。

角量与线量的对应关系

刚体动力学除了线性值之外，还具有角量值。角量和线量是一一对应的关系，就像旋转是平移的”旋转版本”：

姿态（Orientation） ↔ 位置（Position）：姿态描述物体的朝向，位置描述物体的位置
角速度（Angular Velocity） ↔ 线速度（Linear Velocity）：角速度描述旋转的速度，线速度描述移动的速度
角加速度（Angular Acceleration） ↔ 线性加速度（Linear Acceleration）：角加速度描述角速度的变化，线性加速度描述线速度的变化
惯性张量（Inertia Tensor） ↔ 质量（Mass）：惯性张量描述物体抵抗旋转的能力，质量描述物体抵抗移动的能力
角动量（Angular Momentum） ↔ 线性动量（Linear Momentum）：角动量描述旋转的状态，线性动量描述移动的状态
扭矩（Torque） ↔ 力（Force）：扭矩使物体旋转，力使物体移动

理解这种对应关系，有助于我们理解刚体动力学的各个概念。

方向（Orientation）

刚体的朝向可以使用一个旋转矩阵或者四元数来表示，它表示刚体当前姿态相对于初始姿态的旋转。

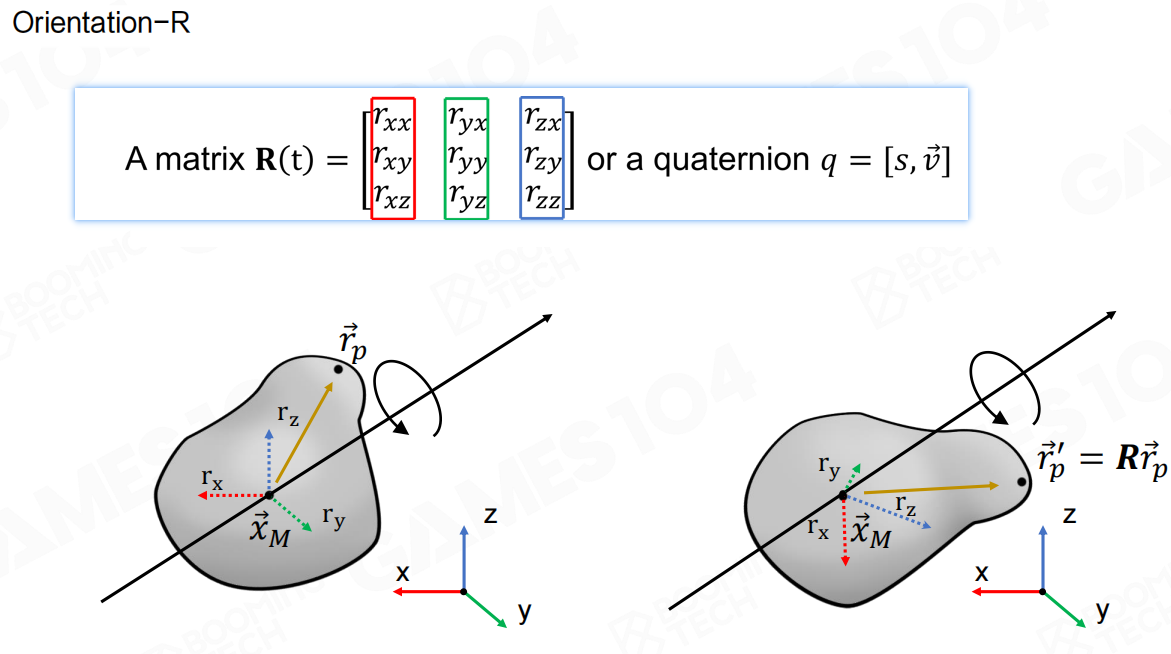
旋转矩阵 R(t) 是一个3×3的矩阵，它的每一列代表物体局部坐标系的一个轴在世界坐标系中的方向。当我们有一个点 rp 在物体的局部坐标系中，通过旋转矩阵可以计算出它在世界坐标系中的位置 rp' = R · rp。

四元数 q = [s, v] 是另一种表示旋转的方式，它由一个标量部分 s 和一个向量部分 v 组成。四元数在游戏引擎中非常常用，因为它避免了旋转矩阵的万向锁问题，而且插值更平滑。

就像位置告诉我们物体在哪里，方向告诉我们物体朝向哪里。一个物体可以保持在同一位置，但改变朝向，就像一个人站在原地转圈。

角速度（Angular Velocity）

角速度表示刚体绕某个旋转轴旋转的速度，需要注意的是在描述角速度时必须要指明旋转轴。

角速度矢量 ω 的方向即为旋转轴的方向，大小等于旋转角度的变化率：

||ω|| = dθ/dt

其中 θ 是以弧度表示的旋转角度。

角速度也可以通过线速度和位置向量来计算：

ω = (v × r) / ||r||²

其中 v 是线速度（向量），r 是从旋转轴到点的位置向量。

角速度的方向遵循右手定则：如果右手四指指向旋转方向，拇指指向的就是角速度的方向。就像地球自转，角速度的方向沿着地轴，从南极指向北极。

角加速度（Angular Acceleration）

角加速度类似于加速度，不过它描述的是角速度的变化。

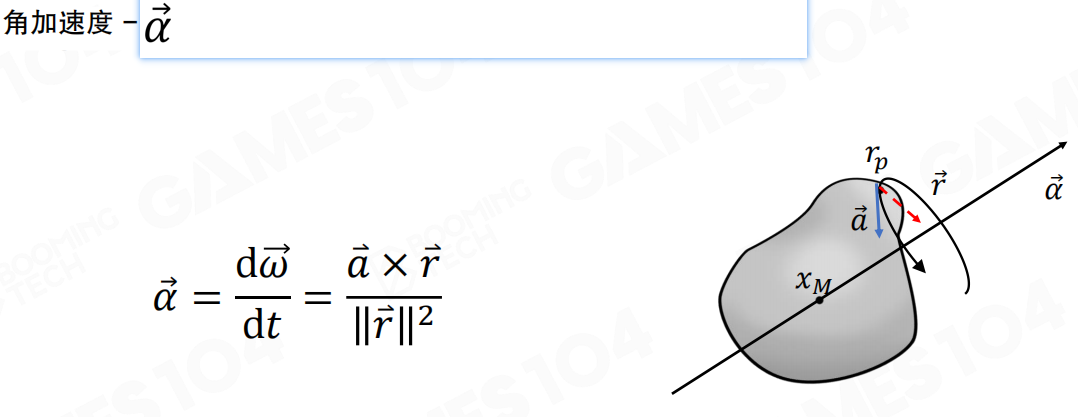
角加速度 α 是角速度对时间的导数：

α = dω/dt = (a × r) / ||r||²

其中 a 是线性加速度（向量），r 是从旋转轴到点的位置向量。

这里需要说明的是，角速度的变化不仅包括绕当前轴转速的变化，它还包括旋转轴发生变化的情况。就像一个陀螺，当它开始倾斜时，旋转轴会改变，角速度也会改变，这就产生了角加速度。

转动惯量（Rotational Inertia）

转动惯量类似于质量，它描述了刚体抵抗旋转的能力。但转动惯量与质量的一大区别在于：转动惯量不是一个常数，而是一个张量（矩阵）。

转动惯量描述了刚体的质量分布。当刚体的朝向发生改变时，需要利用旋转矩阵来计算当前姿态下的转动惯量：

I = R · I₀ · Rᵀ

其中 I₀ 是刚体在主轴坐标系下的转动惯量（通常是对角矩阵），R 是旋转矩阵，Rᵀ 是 R 的转置。

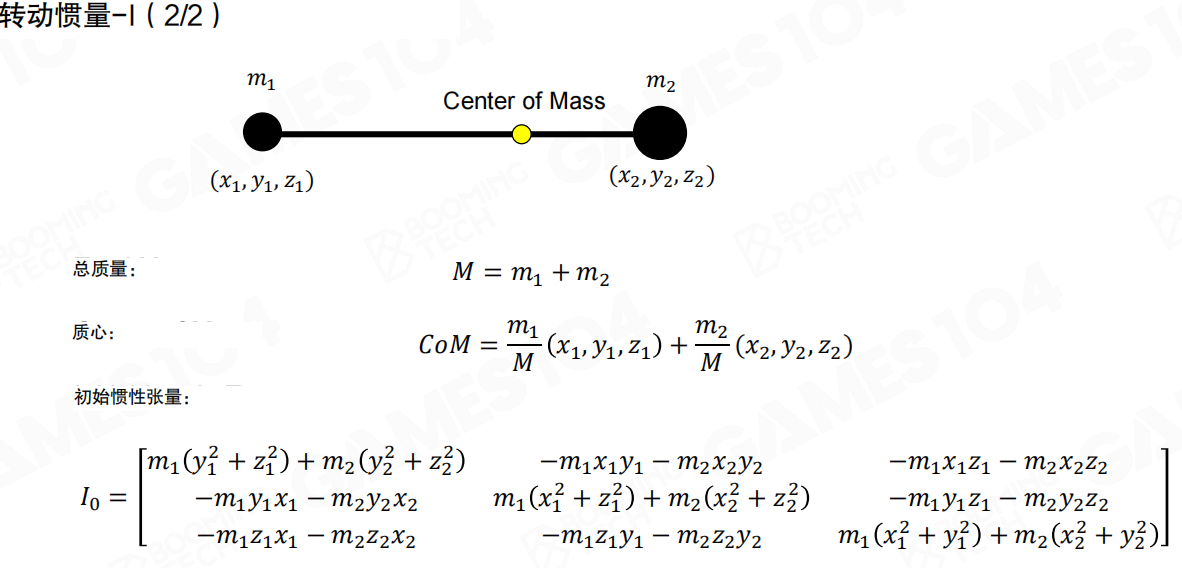
对于两个质点的系统，我们可以计算总质量、质心和初始惯性张量。转动惯量张量 I₀ 是一个3×3的矩阵，它的元素描述了质量在不同方向上的分布。

转动惯量比较难理解，可以这样理解：我们在计算动量时使用的是 m · v，计算角动量时使用的是 I · ω。I（转动惯量）是一个创造出来的变量，类比质量。物体以相同的转速围绕不同的轴心旋转时，其表现出来的动能是不一样的。直观的表现就是：当转速相同时，旋转臂越长，所需的能量越大。可以将物体分解为一个个粒子，相同转速下，每个粒子的速度和其旋转半径相关，离轴心越远的粒子，速度越大，动能也越大。

角动量（Angular Momentum）

角动量描述了刚体旋转的状态，它是转动惯量与角速度的乘积。

角动量的公式为：

L = I · ω

其中 L 是角动量（向量），I 是转动惯量张量（矩阵），ω 是角速度（向量）。

角动量守恒定律告诉我们：在没有外力矩的情况下，角动量保持不变。这就是为什么花样滑冰运动员可以通过改变转动惯量来控制旋转速度。当运动员把手臂收拢时，转动惯量变小，角速度增大，旋转加快；当运动员把手臂展开时，转动惯量变大，角速度减小，旋转变慢。但角动量 L = I · ω 保持不变。

扭矩（Torque）

当外力不通过刚体的质心时会产生力矩，从而导致刚体发生旋转。

扭矩 τ 是位置向量和力的叉积，也等于角动量的变化率：

τ = r × F = dL/dt

其中 r 是从旋转轴到受力点的位置向量，F 是施加在刚体上的外力（向量）。

扭矩使物体发生转动。比如开门时，我们推门的位置离门轴越远，产生的扭矩越大，门越容易打开。虽然扭矩的单位与功的单位相同（N·m），但含义不一样。扭矩是使物体旋转的物理量，而功是使物体移动的物理量。

角量与线量的总结

角量和线量是一一对应的关系，它们的计算公式也类似：

角量	公式	线量	公式
姿态 R	R	位置 x	x
角速度 ω	ω = (v × r) / \|\|r\|\|²	线速度 v	v = dx/dt
角加速度 α	α = dω/dt = (a × r) / \|\|r\|\|²	线性加速度 a	a = dv/dt = d²x/dt²
惯性张量 I	I = R · I₀ · Rᵀ	质量 M	M = Σ mi
角动量 L	L = I · ω	线性动量 p	p = Mv
扭矩 τ	τ = dL/dt	力 F	F = dp/dt = Ma

在质点动力学的基础上把旋转部分也考虑进来，对物体的运动状态进行更新，就得到了刚体动力学的仿真方法。

应用实例：台球动力学

以台球游戏模拟为例，尽管我们已经了解了刚体动力学的基本要素，但轻量级台球游戏中的物理模拟仍然相当复杂。

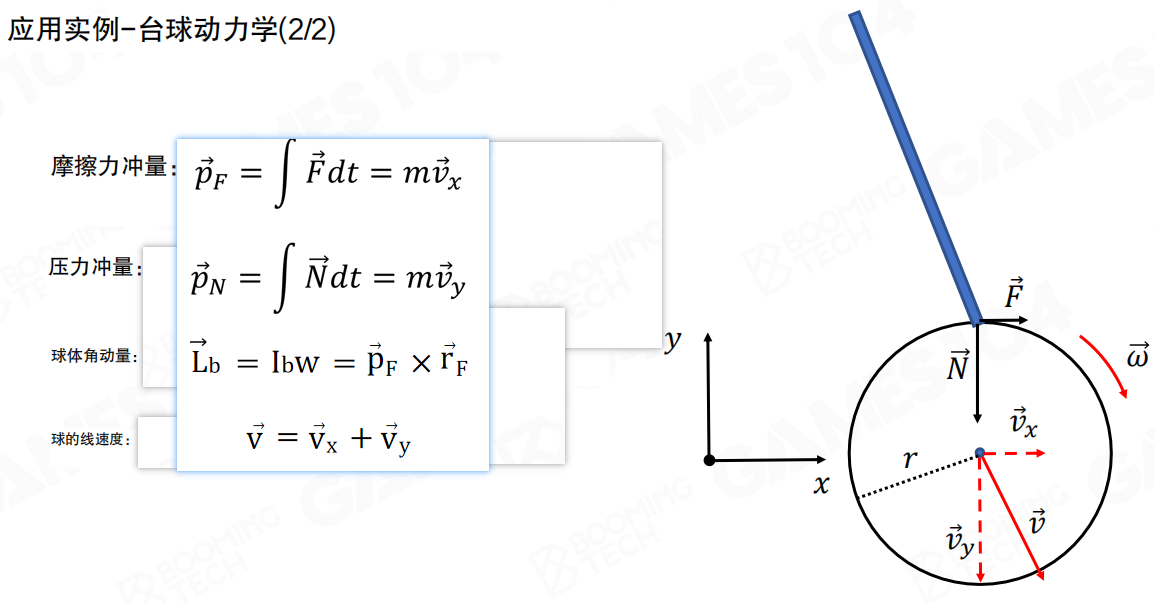
我们假设台球自身与桌面没有摩擦，这样台球的运动可以简化为二维平面运动。在进行仿真时，需要把球杆给予台球的力（冲量）移动到球心来计算台球沿球杆方向的速度；同时这种移动还会对台球施加一个力矩使台球产生旋转，因此也需要更新台球的角速度。

具体来说：

摩擦力冲量 pF = ∫ F dt = mvx：产生水平方向的线速度（向量）
压力冲量 pN = ∫ N dt = mvy：产生垂直方向的线速度（向量）
球体角动量 Lb = Iω = pF × rF：由摩擦力冲量产生（向量）
球的线速度 v = vx + vy：由两个冲量分量合成（向量）

这就是为什么台球在被击打后，既有平移运动，也有旋转运动。旋转会影响球与桌面的摩擦，从而影响球的运动轨迹。

总结

刚体动力学是物理系统的重要组成部分。它扩展了质点动力学，引入了旋转相关的概念：

方向：描述物体的朝向，用旋转矩阵或四元数表示
角速度：描述旋转的速度，方向沿旋转轴
角加速度：描述角速度的变化
转动惯量：描述物体抵抗旋转的能力，是一个张量
角动量：描述旋转的状态，等于转动惯量乘以角速度
扭矩：使物体旋转的物理量，等于位置向量与力的叉积

角量和线量是一一对应的关系，理解这种对应关系有助于我们理解刚体动力学的各个概念。在实际游戏中，刚体动力学让我们能够模拟更真实的物理效果，比如物体的翻滚、旋转、碰撞等。

10.5 碰撞检测

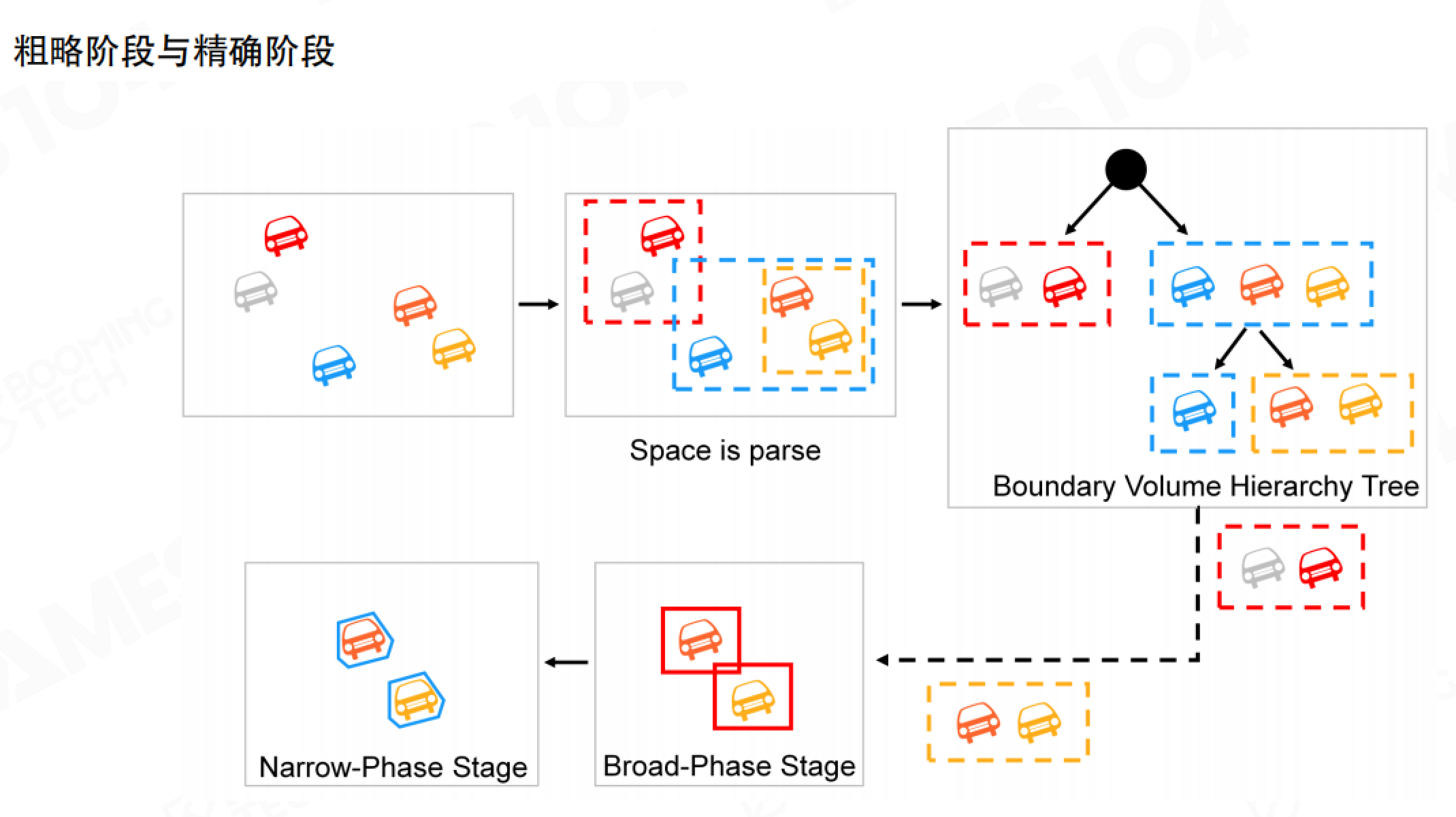
在进行刚体仿真时，我们需要考虑不同刚体之间的相互作用，也就是碰撞问题。要求解碰撞问题，第一步是对刚体碰撞进行检测。如果场景中有1000个物体，每两个物体都要检测一次，就需要检测50万次，这显然太慢了。现代物理引擎通常使用两阶段的检测方法来提高效率。

碰撞检测的两个阶段

碰撞检测分为两个阶段：粗检测阶段（Broad Phase）和窄检测阶段（Narrow Phase）。

粗检测阶段的目标是快速筛选出可能发生碰撞的物体对，使用简单的包围盒（如AABB）进行快速检测。就像用大筛子先筛一遍，把明显不会碰撞的物体对排除掉。

窄检测阶段则对粗检测筛选出的物体对进行精确的碰撞检测，计算碰撞点、碰撞法线、穿透深度等详细信息。就像用细筛子再筛一遍，精确判断是否真的碰撞了。

这种两阶段的方法大大提高了碰撞检测的效率。如果场景中有1000个物体，粗检测可能只筛选出100对需要精确检测的物体，而不是50万对。

粗检测阶段（Broad Phase）

粗检测阶段的目标是快速找出可能发生碰撞的物体对。显然，场景中大部分物体不会同时发生接触，因此粗检测只利用物体的包围盒（Bounding Box）来快速筛选。

在做碰撞检测之前，我们需要用一个对象来表示物体的检测范围，这里我们使用AABB包围盒（Axis-Aligned Bounding Box，轴对齐包围盒）来处理。AABB是一个与坐标轴对齐的长方体，计算简单，非常适合快速检测。

目前物理引擎中常用的粗检测方法包括空间划分（Space Partitioning）和排序扫描（Sort and Sweep）两类方法。

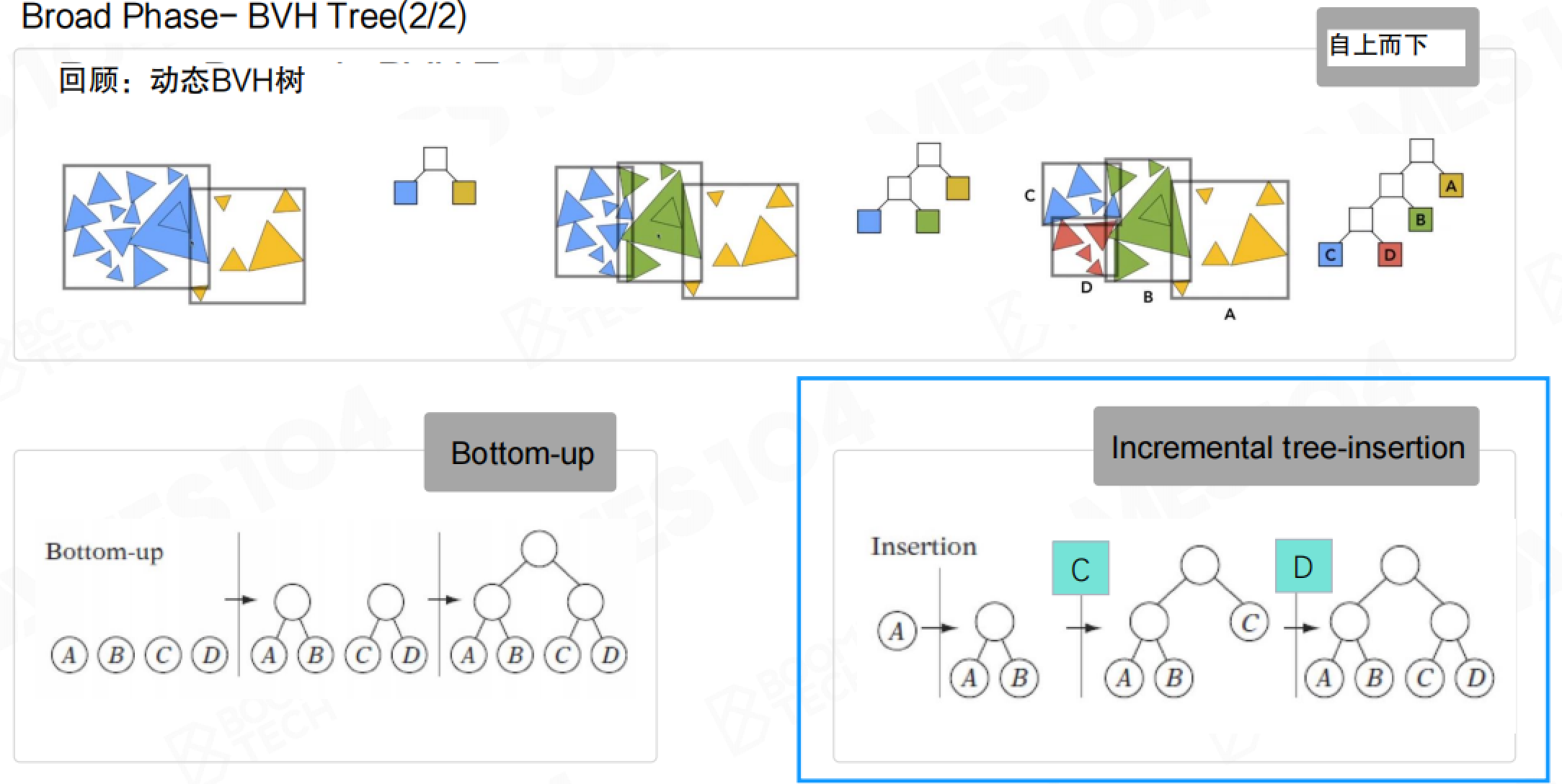
边界体积层次树（BVH Tree）

边界体积层次树（Bounding Volume Hierarchy Tree，BVH树）是空间划分的经典算法。我们在介绍渲染技术时就介绍过空间划分的相关概念，它的思想是把场景中的物体使用一个树状的数据结构进行管理，从而加速判断物体是否相交的过程。

BVH针对空间中的物体进行划分，生成多叉树结构，便于加速碰撞检测等类似功能处理。对包围盒中的物体，在特定维度上对物体进行切分，重新生成包围盒，保证包围盒完全包含所有相应的物体。

BVH树使用一棵二叉树来管理场景中所有物体的包围盒。BVH的特点是它可以通过动态更新节点来描述场景中物体的变化，因此可以快速地检测场景中的包围盒可能存在的碰撞。

BVH树的创建过程可以通过自上而下（Top-down）或自下而上（Bottom-up）的方式。自上而下是从根节点开始，逐步分割空间；自下而上是从叶子节点开始，逐步合并。还有一种增量插入（Incremental tree-insertion）的方法，适合动态场景。

BVH树的优点是物体变化成本低。当场景中的物体移动时，只需要更新相关的节点，而不需要重建整个树。这使得BVH树非常适合动态场景。

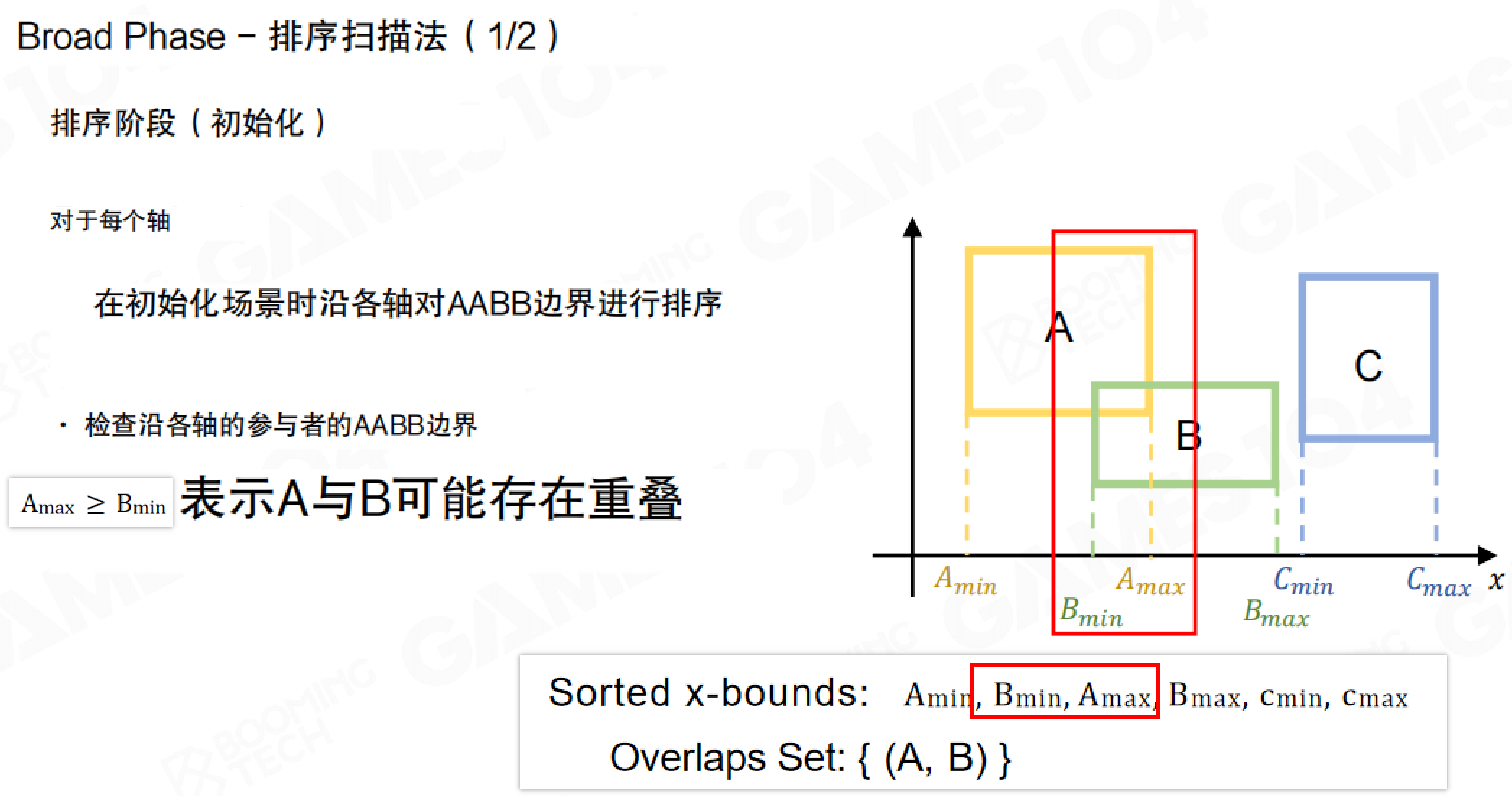
排序扫描法（Sort and Sweep）

排序扫描法（Sort and Sweep）是使用排序来检测碰撞的算法，它的思想非常直观：对于使用AABB进行表示的包围盒，两个包围盒出现碰撞时必然会导致它们的边界产生了重叠，而判断是否出现重叠则可以通过对包围盒的边界进行排序来进行计算。

这种方法的思想很简单：在每个维度上（x、y、z）对每个物体的区域范围进行检测，判断是否存在交集。当两个区域在所有维度上都存在交集，则两者相交。

在排序阶段（初始化），对于每个轴，在初始化场景时沿各轴对AABB边界进行排序。检查沿各轴的参与者的AABB边界，如果 Amax ≥ Bmin，表示A与B可能存在重叠。

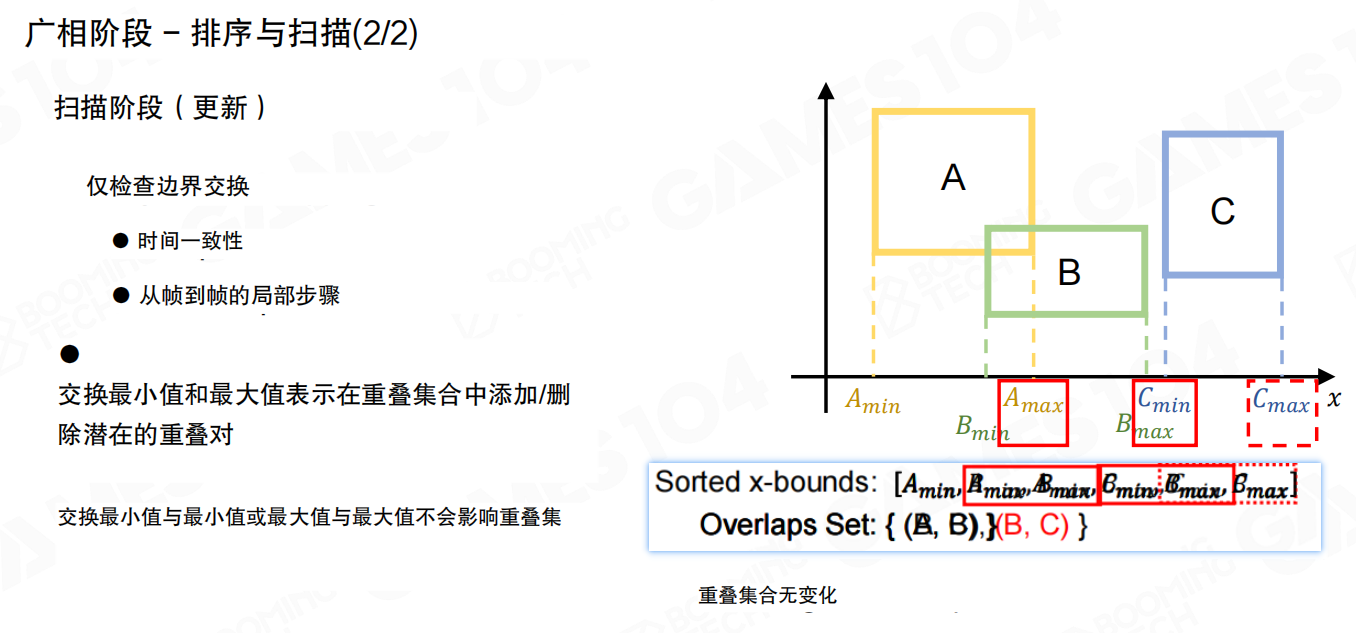
在扫描阶段（更新），只需要检查边界交换。这利用了时间一致性（Temporal coherence）：从帧到帧的局部步骤。交换最小值和最大值表示在重叠集合中添加/删除潜在的重叠对。交换最小值与最小值或最大值与最大值不会影响重叠集。

排序扫描法的效率很高，因为它利用了帧与帧之间的连续性，只需要处理发生变化的边界，而不需要每帧都重新排序。

窄检测阶段（Narrow Phase）

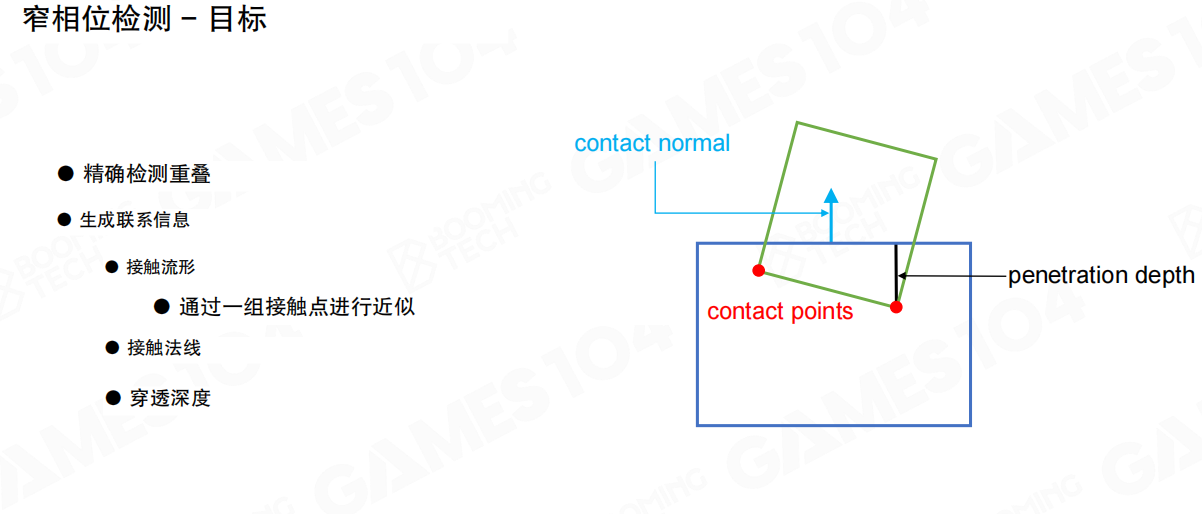
筛选出可能发生碰撞的物体后，就需要对它们进行实际的碰撞检测，这个阶段称为窄检测阶段（Narrow Phase）。除了进一步判断刚体是否相交外，在窄检测中一般还需要计算交点、相交深度以及方向等信息。

窄检测阶段的目标包括：

精确检测重叠：准确判断两个物体是否真的发生了碰撞
生成联系信息：
- 接触流形（Contact Manifold）：通过一组接触点进行近似
- 接触法线（Contact Normal）：碰撞的方向
- 穿透深度（Penetration Depth）：物体相互穿透的深度

目前在窄检测中一般会使用相交测试（Intersection Test）、Minkowski差集（Minkowski Difference）以及分离轴定理（Separating Axis Theorem）等方法。

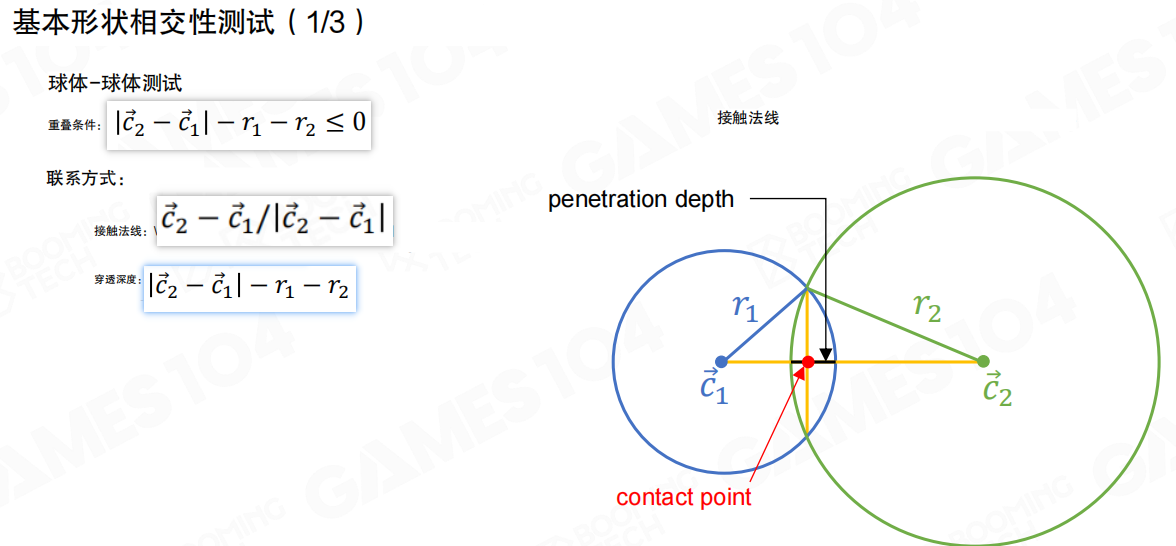
基本形状相交测试（Basic Shape Intersection Test）

对于一些简单的几何形状，可以使用解析的方法来判断它们是否相交，并且计算交点的信息。

球体-球体测试：

重叠条件：|c₂ - c₁| - r₁ - r₂ ≤ 0

其中 c₁ 和 c₂ 是两个球体的中心（向量），r₁ 和 r₂ 是它们的半径。如果两个球心之间的距离小于等于半径之和，则发生重叠。

接触法线：(c₂ - c₁) / |c₂ - c₁|

接触法线是从第一个球心指向第二个球心的归一化向量。

穿透深度：|c₂ - c₁| - r₁ - r₂

穿透深度表示两个球体相互穿透的距离。如果这个值为负，说明没有穿透；如果为正，说明发生了穿透。

球体-胶囊体测试：

胶囊体由一个圆柱体和两个半球体组成。测试时，我们需要找到胶囊体内部线段上距离球心最近的点 L。

重叠条件：|C - L| - rs - rc ≤ 0

其中 C 是球心（向量），L 是胶囊体内部线段上的最近点（向量），rs 是球体半径，rc 是胶囊体半径。

接触法线：(L - C) / |L - C|

穿透深度：|C - L| - rs - rc

胶囊体-胶囊体测试：

向量 L₁ 和 L₂ 是两条线段上最接近的点。

重叠条件：|L₂ - L₁| - r₁ - r₂ ≤ 0

接触法向量：(L₂ - L₁) / |L₂ - L₁|

穿透深度：|L₂ - L₁| - r₁ - r₂

基本形状相交测试的优点是计算简单、效率高，但只适用于简单的几何形状。对于复杂的凸多边形或凸多面体，需要使用更通用的方法。

基于Minkowski差集的方法（Minkowski Difference-based Methods）

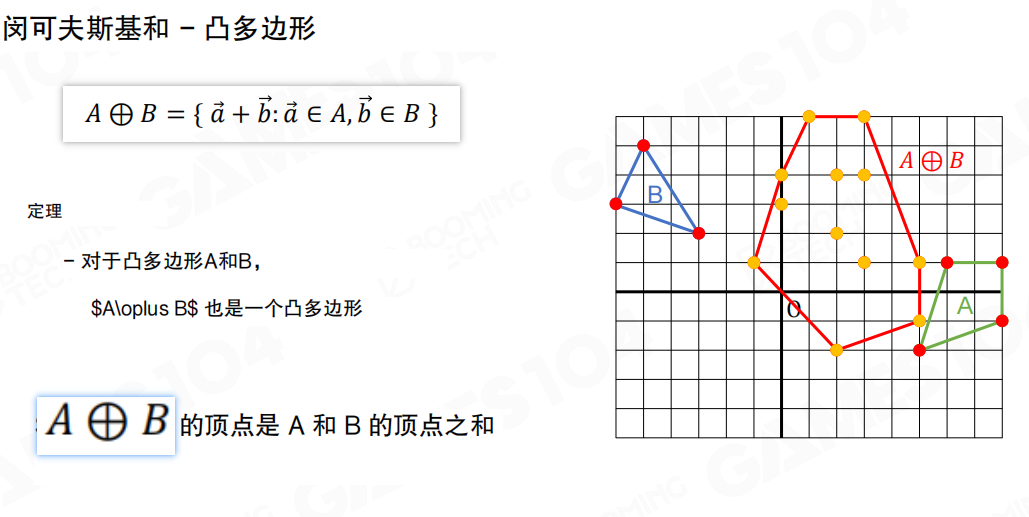
对于凸多边形的情况，可以使用Minkowski差集（Minkowski Difference）来判断它们是否相交。在介绍Minkowski差集之前，首先要引入Minkowski和（Minkowski Sum）的概念。

Minkowski和的定义是：来自A的点集 + 来自B的点集 = A和B的Minkowski和中的点集。

数学定义：A ⊕ B = { a + b : a ∈ A, b ∈ B }

也就是说，Minkowski和是两个集合中任意一对向量相加后得到的新的点集。就像把集合A中的每个点，都按照集合B中每个点的方向移动，得到的所有可能位置的集合。

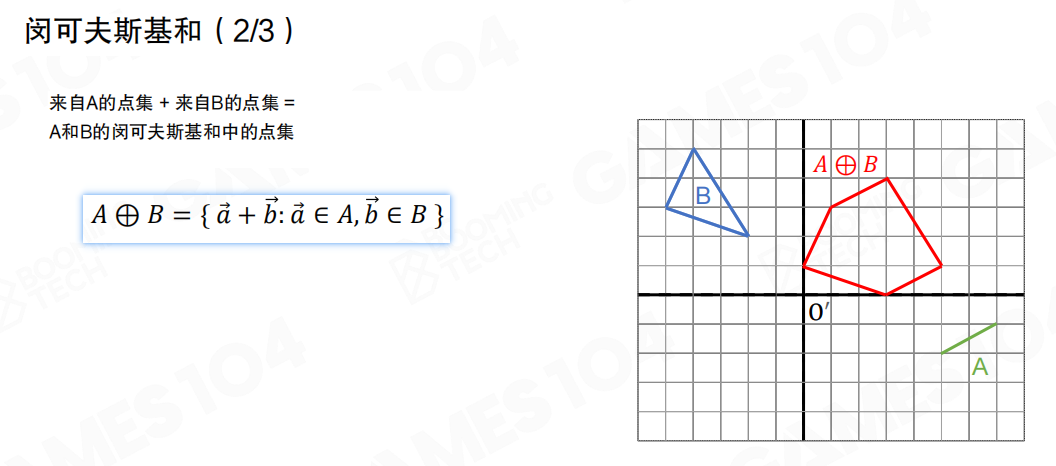
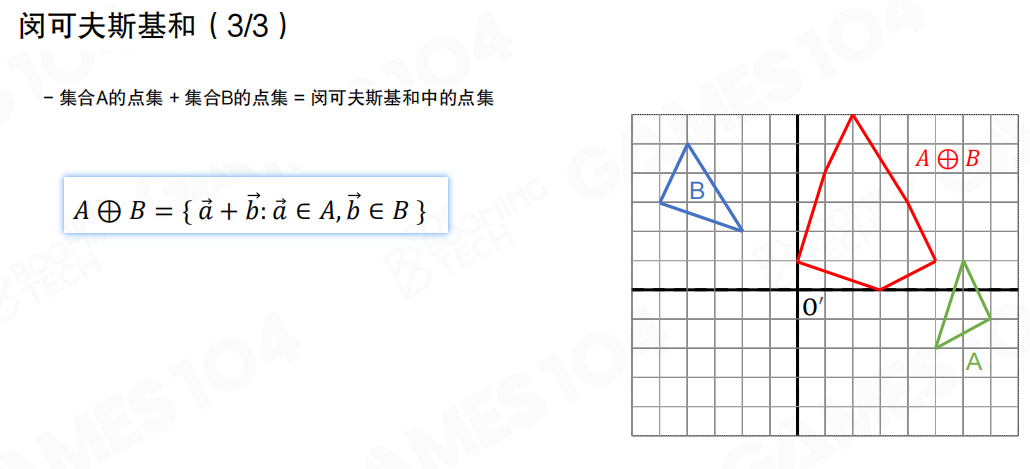
对于凸多边形，它们的Minkowski和也必为一个凸多边形，而且这个新多边形的顶点也是原始多边形顶点的和。Minkowski和的本质是两个集合相交的凸包。

在此基础上，我们定义点集A和B的Minkowski差集为A与镜像B的Minkowski和，即：

A ⊖ B = A ⊕ (-B)

其中 -B 是B关于原点的镜像。

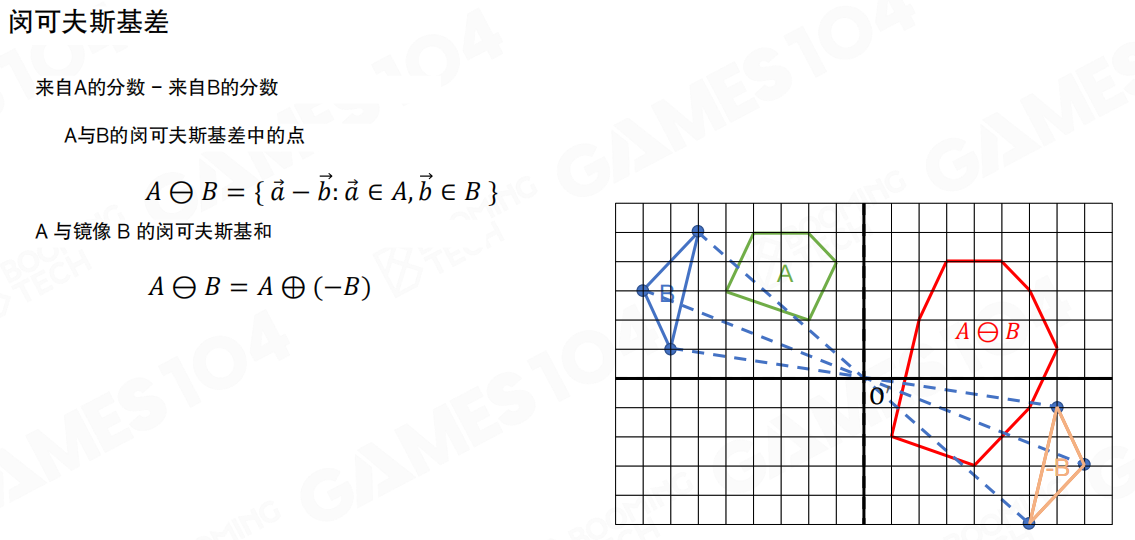
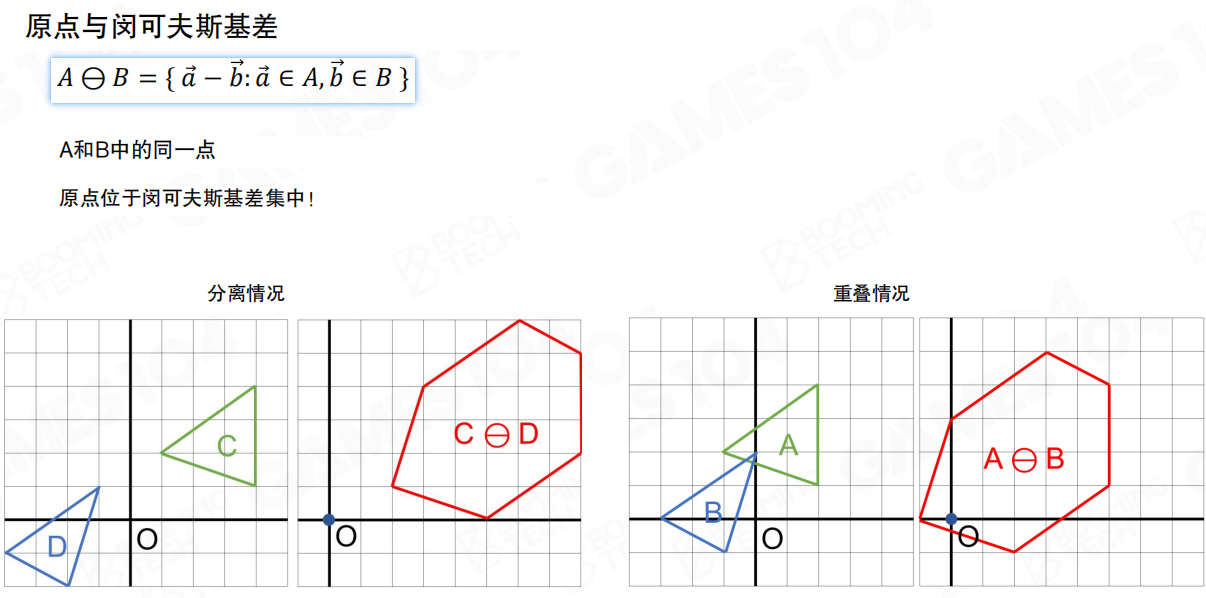
可以证明：若两个集合相交，则Minkowski差集包含原点。这样，判断两个凸多边形是否相交的问题就转化为判断原点是否位于凸多边形中的问题。

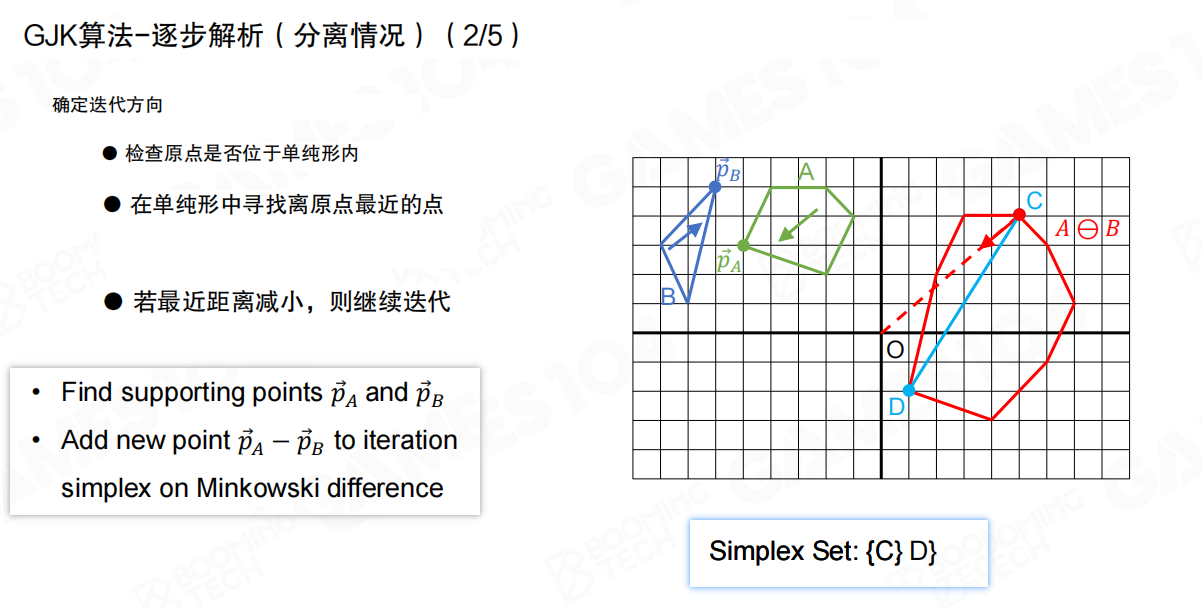
GJK算法（Gilbert-Johnson-Keerthi Algorithm）就是用来判断凸包区域是否包含原点的算法。

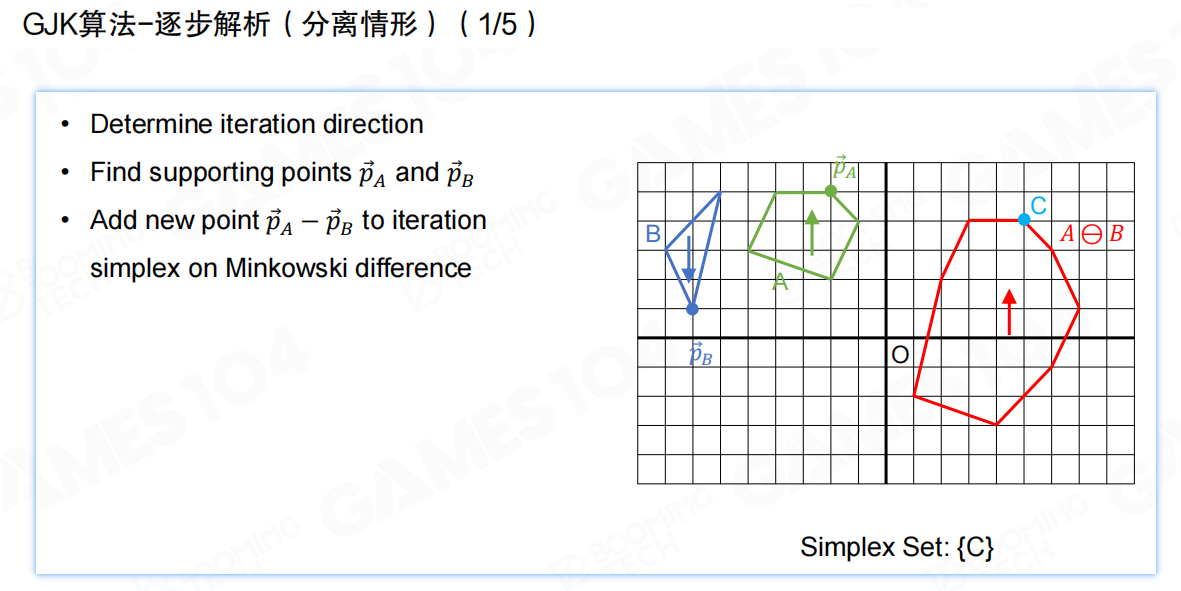
GJK算法的核心思想是：在Minkowski差集中构建一个单纯形（Simplex），逐步逼近原点。如果单纯形包含原点，说明两个物体相交；如果无法包含原点，说明两个物体分离。

GJK算法的主要流程如下：

确定迭代方向：检查原点是否位于单纯形内；在单纯形中寻找离原点最近的点；若最近距离减小，则继续迭代
查找支撑点：找到支撑点 pA 和 pB
添加新点：将新点 pA - pB 添加到迭代单纯形中

对于分离情况，算法会逐步构建单纯形，直到确定原点不在Minkowski差集中，从而判断两个物体分离。

对于重叠情况，算法会在单纯形中找到包含原点的点，从而判断两个物体相交。

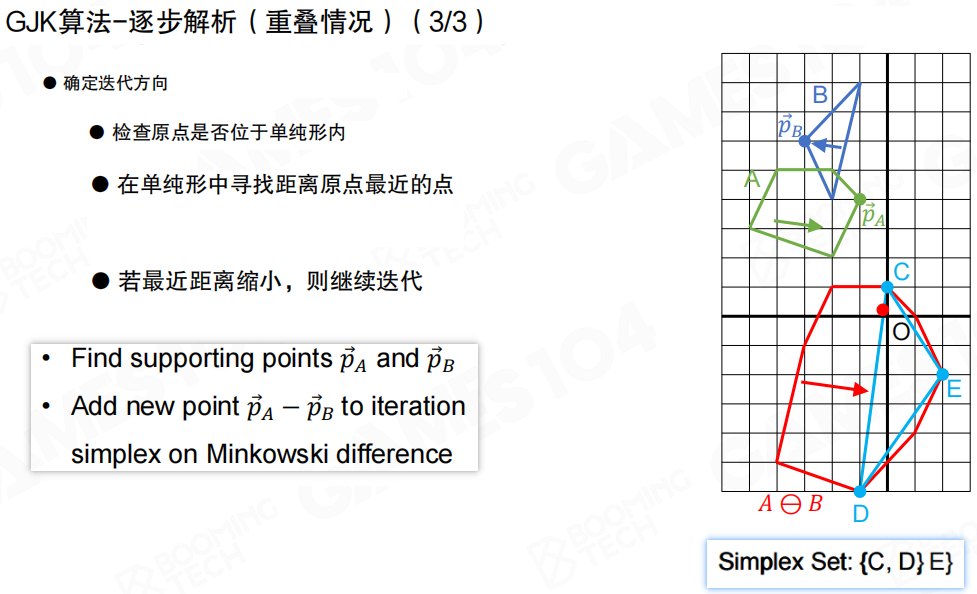
当GJK算法判断出两个凸多边形相交后，还可以进一步计算交点以及深度等信息。

分离轴定理（Separating Axis Theorem，SAT）

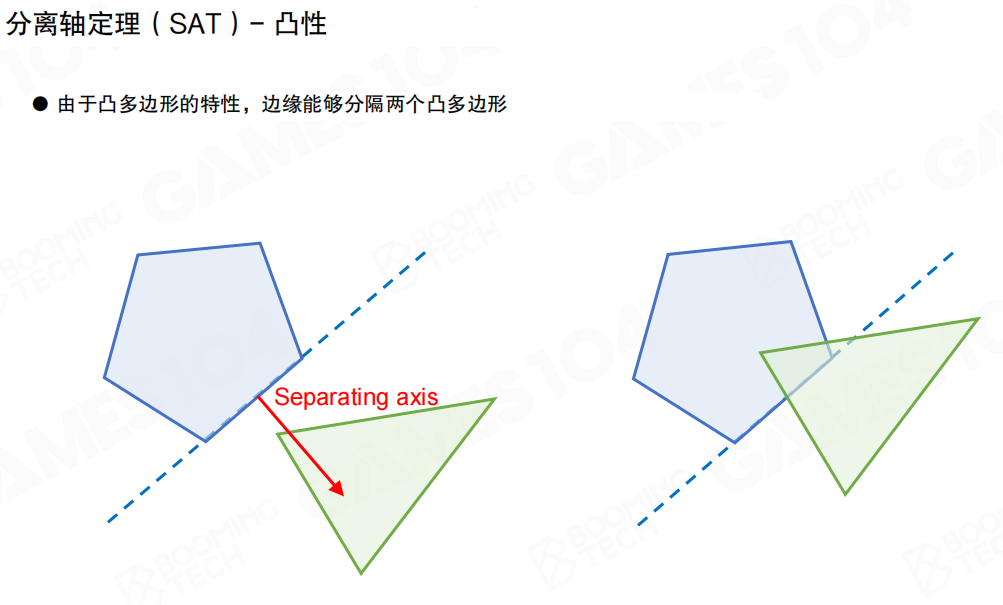
分离轴定理（Separating Axis Theorem，SAT）同样是一种计算凸多边形相交的算法。它的核心思想是：对于两个凸多面体，一定可以存在一条边或面将两者完全分离。

由于凸多边形的特性，边缘能够分隔两个凸多边形。平面上任意两个互不相交的图形，我们必然可以找到一条直线将它们分隔在两端。对于凸多边形还可以进一步证明：必然存在以多边形顶点定义的直线来实现这样的分隔，因此判断凸多边形相交就等价于寻找这样的分隔直线。

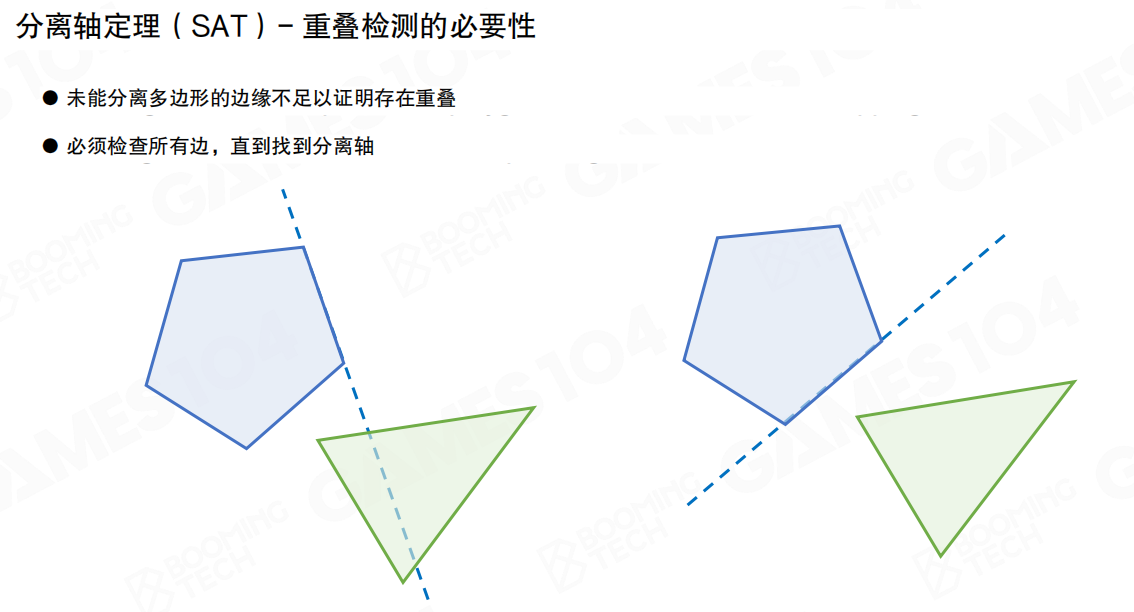
未能分离多边形的边缘不足以证明存在重叠。必须检查所有边，直到找到分离轴。

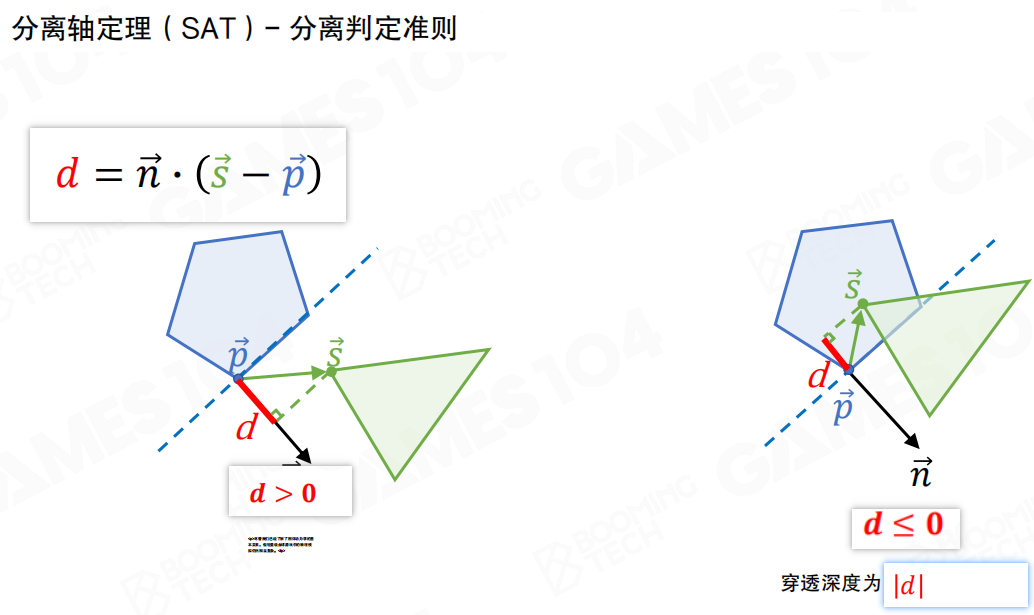
分离判定准则：d = n · (s - p)

其中 n 是分离轴的法向量（向量），s 和 p 是两个物体在分离轴上的支撑点（向量），· 表示点积。

如果 d > 0，说明两个物体分离；如果 d ≤ 0，说明两个物体重叠，此时穿透深度为 |d|。

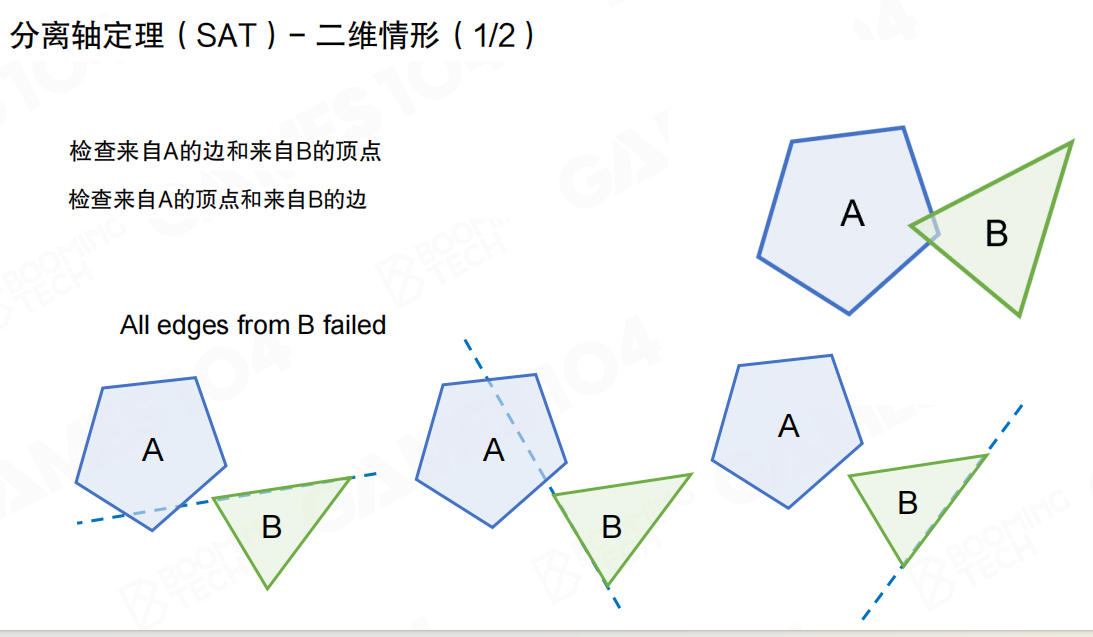
二维情况（2D Case）：

使用SAT判断凸多边形是否相交时，需要分别对两个图形的边进行遍历，然后判断另一个图形上的每个顶点是否落在边的同一侧。

检查来自A的边和来自B的顶点
检查来自A的顶点和来自B的边

只要发现存在一条边可以分隔两个图形，即说明它们互不相交，否则继续遍历直到用尽所有的边，此时两个图形必然是相交的。

算法流程：

for each edge eA from A do
  overlapped = false
  for each vertex vB from B do
    if projection of vB on normal of eA <= 0 then
      overlapped = true, break
    end if
  end for
  if not overlapped then
    A and B are separated, terminate
  end if
end for
// 类似地检查B的边

当图形的位置发生变化时，还可以从上一次检测得到的分离轴开始重新进行检测，这样可以进一步提高算法的效率。

SAT优化：

可以通过缓存上一次的分离轴来优化算法。在检测时，首先检查上一次的分离轴是否仍然有效，如果有效则直接返回分离结果，这样可以大大提高算法的效率。

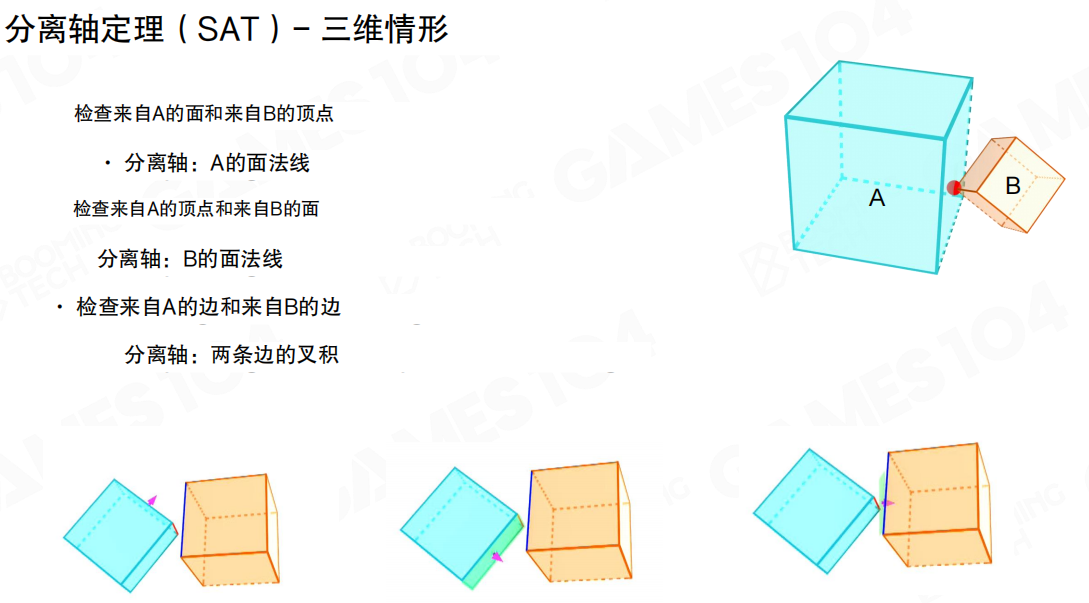
三维情况（3D Case）：

对于三维图形的情况，则不仅需要考虑面和面的分隔关系，还要考虑边和边的分隔关系：

检查来自A的面和来自B的顶点：分离轴是A的面法线
检查来自A的顶点和来自B的面：分离轴是B的面法线
检查来自A的边和来自B的边：分离轴是两条边的叉积

总结

碰撞检测是物理系统的重要组成部分，它分为两个阶段：

粗检测阶段：快速筛选出可能发生碰撞的物体对
- BVH树：使用树状结构管理空间，适合动态场景
- 排序扫描法：利用排序和帧间连续性，效率很高
窄检测阶段：精确检测碰撞并生成联系信息
- 基本形状相交测试：适用于简单几何形状，计算简单高效
- 基于Minkowski差集的方法：适用于凸多边形，使用GJK算法判断是否相交
- 分离轴定理（SAT）：适用于凸多边形，通过寻找分离轴判断是否相交

不同的方法适用于不同的场景。选择合适的碰撞检测方法，可以在保证准确性的同时，大大提高物理系统的运行效率。

10.6 碰撞解决

完成碰撞检测后，我们已经精确地确定了碰撞，也获取了碰撞信息。但检测到碰撞只是第一步，接下来我们需要处理碰撞解决，让发生碰撞的物体相互分开，避免它们继续穿透。

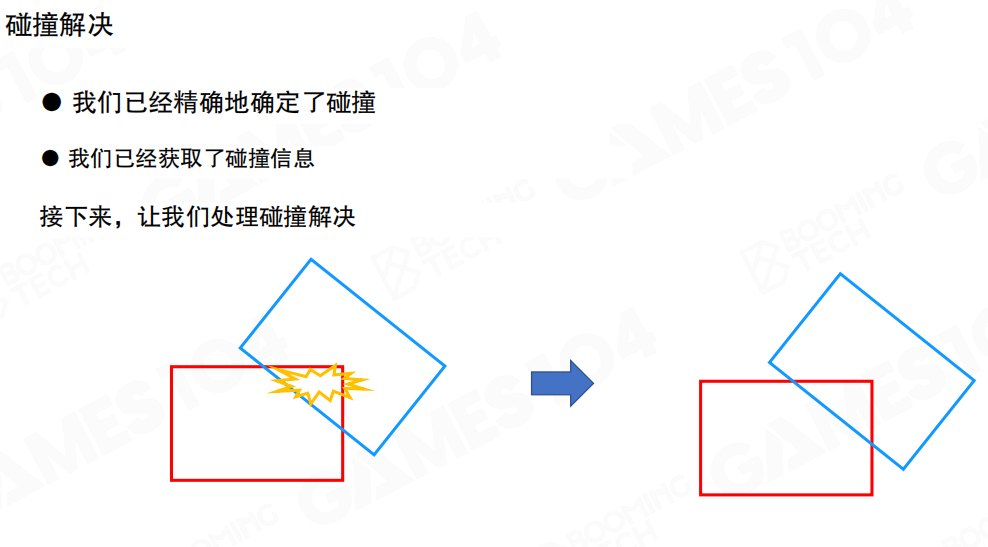
碰撞解决的目标是：当两个物体发生碰撞并相互穿透时，通过某种方法将它们分开，恢复到不重叠的状态。就像两个球相撞后，它们应该弹开，而不是继续重叠在一起。

碰撞解决的三种方法

目前刚体的碰撞主要有三种处理思路：

施加惩罚力（Penalty Force）：通过施加力来分离物体
求解速度约束（Solve Velocity Constraints）：通过约束求解来调整速度
求解位置约束（Solve Position Constraints）：通过约束求解来调整位置（将在下一讲中详述）

在现代物理引擎中，约束求解（Constraints）方法更常用，因为它更稳定、更准确。惩罚力方法虽然直观，但存在很多问题，现代引擎中几乎不再使用。

施加惩罚力（Penalty Force）

施加惩罚力是最直观的碰撞处理方法，它的思想是：当两个物体相交后，沿反方向分别施加一个排斥力把它们推开。

这种方法的特点：

在游戏中很少使用：虽然思想简单，但实际效果不理想
需要施加较大的作用力和较小的时间步长：为了快速分离物体，需要很大的力；为了稳定，需要很小的时间步长，这会大大增加计算量
需要让碰撞的物体看起来刚硬：如果力不够大，物体会显得”软”，穿透会持续存在

惩罚力方法的问题在于：它要求设置比较大的排斥力以及很小的积分时间间隔，否则容易出现非常不符合直觉的碰撞效果。比如物体可能会”弹跳”过度，或者穿透问题无法完全解决。因此，现代物理引擎中几乎不会使用惩罚力来处理刚体碰撞问题。

求解速度约束（Solve Velocity Constraints）

目前物理引擎中主流的刚体碰撞处理算法是基于拉格朗日力学（Lagrangian Mechanics）的求解方法。它会把刚体之间的碰撞和接触转换为系统的约束，然后求解约束优化问题。

拉格朗日力学仍然属于牛顿力学范畴，只不过以不同的视角对力的理解，更便于在计算机中应用。经典力学着重分析位移、速度、加速度、力等矢量间的关系。拉格朗日力学对于特定约束下的运动，从能量转化的角度来处理运动状态。这样就可以避免繁琐的受力分析。

拉格朗日力学将碰撞问题转化为约束问题。碰撞约束包括：

非穿透性（Non-penetration）：两个物体不能相互穿透
恢复系数（Coefficient of Restitution）：控制碰撞后的反弹程度
摩擦力（Friction）：控制物体接触时的滑动阻力

通过迭代求解器（Iterative Solver），我们可以逐步求解这些约束，得到满足所有约束条件的最终状态。

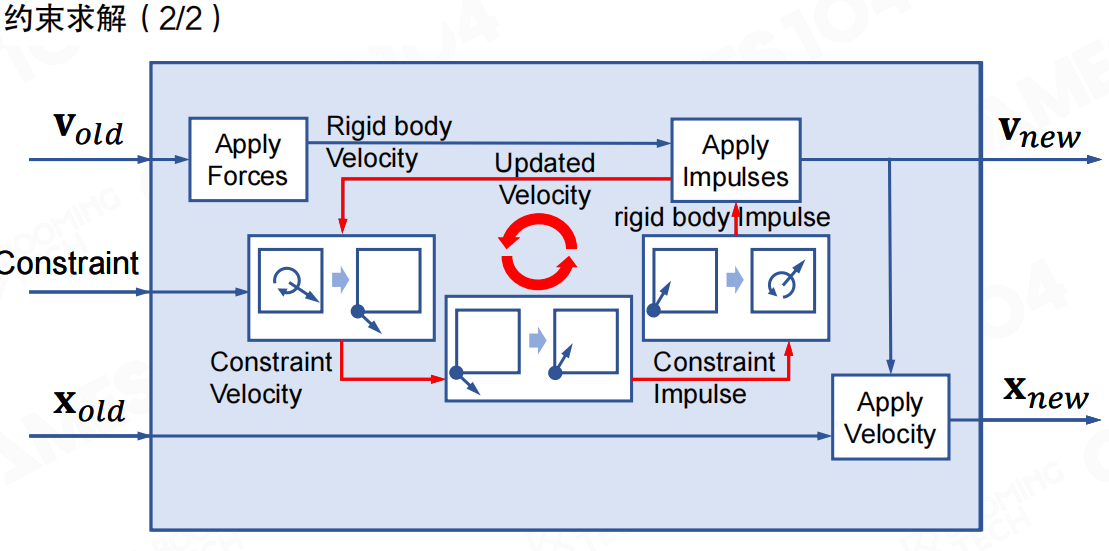
约束求解的流程大致如下：

应用力（Apply Forces）：根据当前状态计算并应用外力，得到刚体的速度
计算约束速度（Constraint Velocity）：根据约束条件计算约束速度
迭代求解（Updated Velocity）：通过迭代求解器，不断更新速度，直到满足所有约束条件
应用冲量（Apply Impulses）：将约束冲量应用到刚体上，得到新的速度
应用速度（Apply Velocity）：使用新的速度更新位置

这个过程是一个迭代过程，通过不断调整速度，最终使所有约束都得到满足。

求解速度约束的方法：

顺序脉冲法（Sequential Impulse Method）：逐个处理每个约束，逐步调整速度
半隐式积分（Semi-implicit Integration）：使用半隐式积分方法，保证数值稳定性

非线性高斯-赛德尔法（Nonlinear Gauss-Seidel Method）的特点：

在多数情况下快速且稳定：能够快速收敛到满足约束的解
广泛应用于大多数物理引擎：是现代物理引擎的标准方法

在求解速度约束时，我们会在接触点施加约束冲量（Constraint Impulse），比如 P_c1 和 P_c2，这些冲量会改变物体的速度，使它们满足非穿透性约束。

总结

碰撞解决是物理系统的重要组成部分。当检测到碰撞后，我们需要将相互穿透的物体分开：

施加惩罚力：通过施加力来分离物体，虽然直观但效果不稳定，现代引擎中很少使用
求解速度约束：基于拉格朗日力学的约束求解方法，将碰撞转化为约束问题，通过迭代求解器逐步调整速度，这是现代物理引擎的主流方法

约束求解方法比惩罚力方法更稳定、更准确，能够更好地处理复杂的碰撞场景。通过将碰撞问题转化为约束优化问题，我们可以更优雅地解决物体之间的相互作用。

10.7 场景查询

除了碰撞检测和碰撞解决外，在游戏中我们往往还需要对场景中的物体进行一些查询操作。这些查询操作也需要物理引擎的支持，它们可以帮助我们实现很多游戏功能，比如子弹击中目标、角色移动检测、爆炸范围检测等。

场景查询主要有三种方式：射线投射（Raycast）、扫描（Sweep）和重叠检测（Overlap）。每种方式都有其特定的应用场景。

射线投射（Raycast）

射线投射（Raycast）是非常基本的查询操作，我们希望能够获取某条射线在场景中击中的物体。实际上在光线追踪中就大量使用了射线投射的相关操作，而在物理引擎中射线投射也有大量的应用。

射线投射将用户自定义的射线与整个场景进行相交检测。可以定义点、方向、距离和查询模式。就像从枪口发射一条射线，看看这条射线会击中哪些物体。

当我们向场景中发射一个子弹，想要知道子弹会射中哪些物体，这就是射线投射功能。在游戏中，射线投射常用于弹道计算、碰撞检测，思想类似光线追踪。

在游戏中，射线投射有广泛的应用。比如在射击游戏中，当玩家开枪时，从枪口发射一条射线，检测这条射线击中的第一个目标，就可以判断子弹是否命中。射线投射还可以用于视线检测，判断角色是否能看到某个目标。

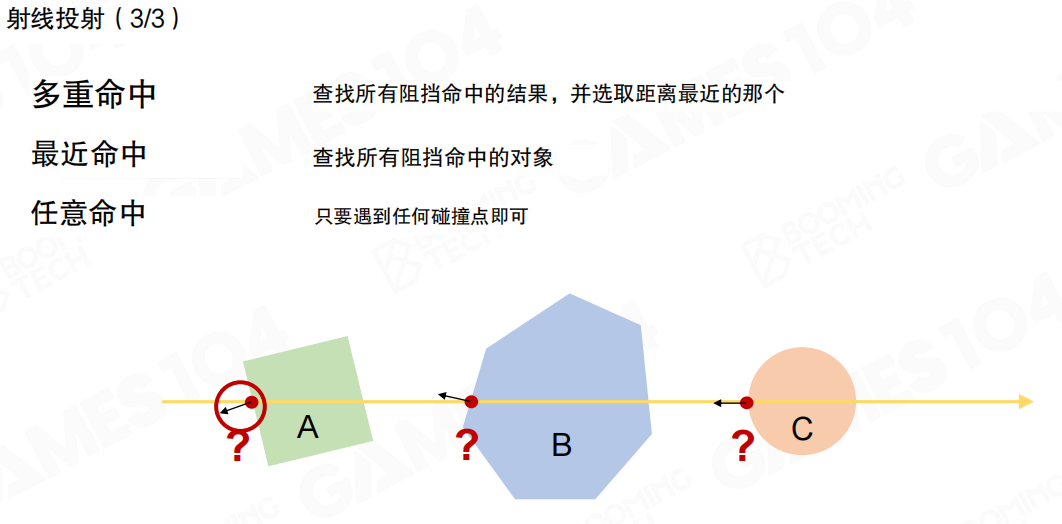
射线投射有三种命中类型：

多重命中（Multiple Hits）：返回所有与射线相交的物体，包括所有进入和退出点
最近命中（Closest Hit）：查找所有阻挡命中的结果，并选取距离最近的那个
任意命中（Any Hit）：只要遇到任何碰撞点即可，通常用于快速判断是否有物体阻挡

当需要知道首个检测到的对象时，就需要进行排序处理，选择最近命中模式。任意命中模式则用于快速判断，不需要知道具体是哪个物体，只需要知道是否有物体阻挡即可。

扫描（Sweep）

扫描（Sweep）与射线投射类似，不过在扫描中需要使用有一定几何形态的物体来检测场景中的其它物体。

扫描的几何形态类似于射线检测，但可以定义形状与姿态。可定义的形状包括：盒体、球体、胶囊体和凸体。

扫描就像用一个有体积的物体沿着某个方向移动，检测这个移动过程中会与哪些物体发生碰撞。这比射线投射更准确，因为考虑了物体的体积。

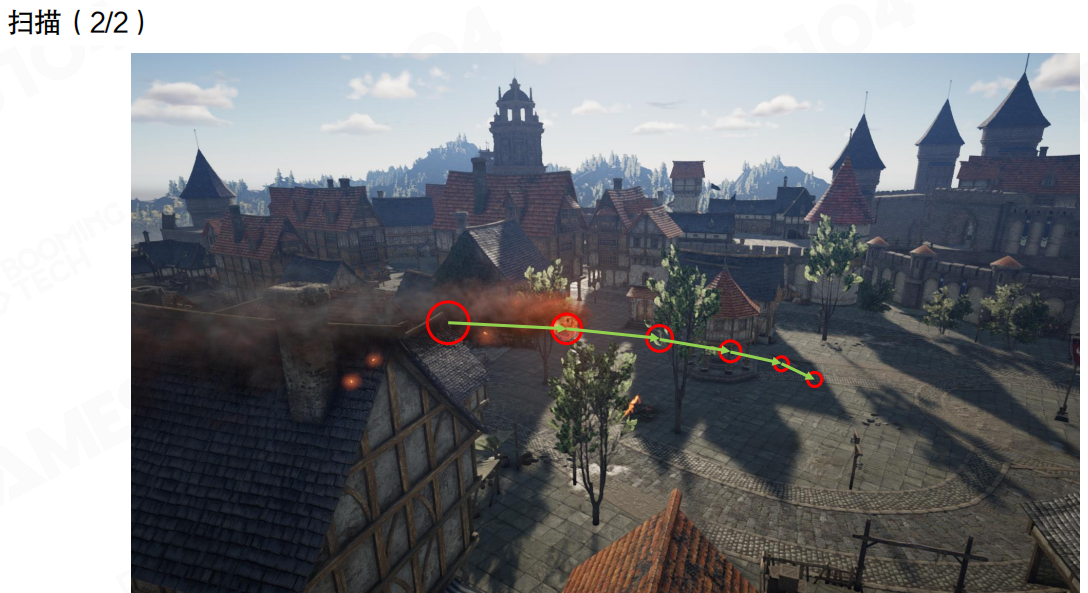
扫描在游戏中有很多应用。比如我们的角色在移动过程中，可以看做是一个胶囊体的Transform，需要实时检测与其它物体的碰撞。当角色移动时，我们用胶囊体进行扫描，检测移动路径上是否有障碍物，如果有，就停止移动或调整移动方向。

扫描还可以用于预测碰撞，比如在角色控制器中，我们可以提前扫描角色的移动路径，判断是否会与墙壁碰撞，从而避免角色穿墙。

重叠检测（Overlap）

重叠检测（Overlap）是另一种常用的操作，此时我们需要判断场景中的物体是否位于某个几何形状中。

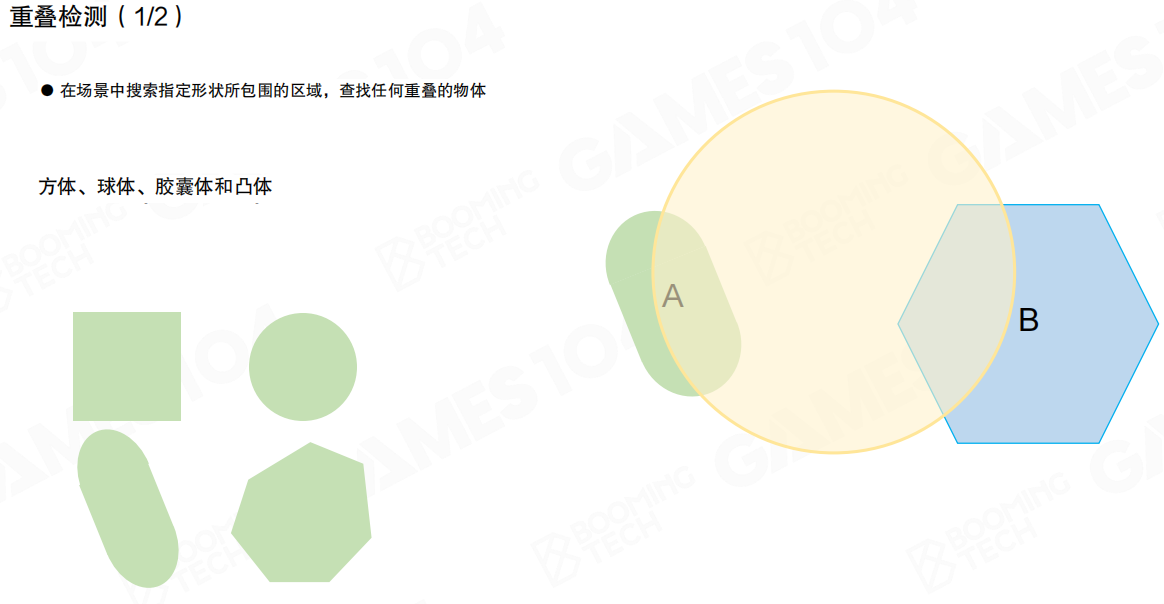
重叠检测在场景中搜索指定形状所包围的区域，查找任何重叠的物体。可使用的形状包括：方体、球体、胶囊体和凸体。

重叠检测与碰撞检测非常类似，不过重叠检测一般只会使用简单的几何体来进行检测。重叠检测不关心物体是否真的碰撞，只关心物体是否在指定的区域内。

当场景中出现范围受力情况，就需要重叠检测来处理。比如爆炸时，创建一个重叠检测来检测处理受影响的对象。我们在爆炸中心创建一个球形或圆柱形的检测区域，所有在这个区域内的物体都会受到爆炸的影响。

重叠检测还可以用于区域触发，比如当玩家进入某个区域时触发事件，或者检测某个区域内有多少敌人等。

碰撞组（Collision Group）

在物理引擎中还需要额外注意对场景中的物体进行分组，这样可以提高各种物理仿真算法的效率。

碰撞组（Collision Group）允许我们给场景中的物体分类，不同的物体属于不同的碰撞组。角色拥有碰撞组属性，比如：

玩家：Pawn（兵卒）
障碍物：Static（静态）
可移动箱子：Dynamic（动态）
触发器盒子：Trigger（触发器）

场景查询可筛选碰撞组。在碰撞检测时，有些对象是不需要进行检测的，比如射线投射会直接跳过触发器，这就是分组的作用（给对象加Tag）。

比如：

玩家移动查询碰撞组：（Pawn、Static、Dynamic）- 玩家移动时需要检测与玩家、静态物体和动态物体的碰撞，但不需要检测触发器
触发器查询碰撞组：（Pawn）- 触发器只需要检测与玩家的交互，不需要检测其他物体

通过碰撞组，我们可以精确控制哪些物体之间需要进行碰撞检测，哪些不需要。这大大提高了物理系统的效率，避免了不必要的计算。

总结

场景查询是物理系统的重要组成部分，它提供了三种主要的查询方式：

射线投射：用一条射线检测场景中的物体，适用于弹道计算、视线检测等
扫描：用一个有体积的物体沿着路径移动，检测碰撞，适用于角色移动检测、预测碰撞等
重叠检测：检测某个区域内有哪些物体，适用于爆炸效果、区域触发等

通过碰撞组，我们可以对场景中的物体进行分类，精确控制哪些物体之间需要进行检测，从而提高物理系统的效率。

场景查询与碰撞检测不同，碰撞检测是物理系统自动进行的，而场景查询是游戏逻辑主动发起的查询操作。两者结合，共同构成了完整的物理系统功能。

10.8 效率，准确性与确定性

物理仿真是极其消耗计算资源的，如果在所有时刻都对场景中的物体进行模拟会造成计算资源的浪费。同时，物理仿真还需要考虑准确性和确定性的问题。本节课最后讨论了物理仿真中的一些优化技巧和重要概念。

模拟优化：孤岛（Island）

我们知道物理仿真是极其消耗计算资源的，如果在所有时刻都对场景中的物体进行模拟会造成计算资源的浪费。因此一种常用的手段是把场景中的物体划分为若干个孤岛（Island）。

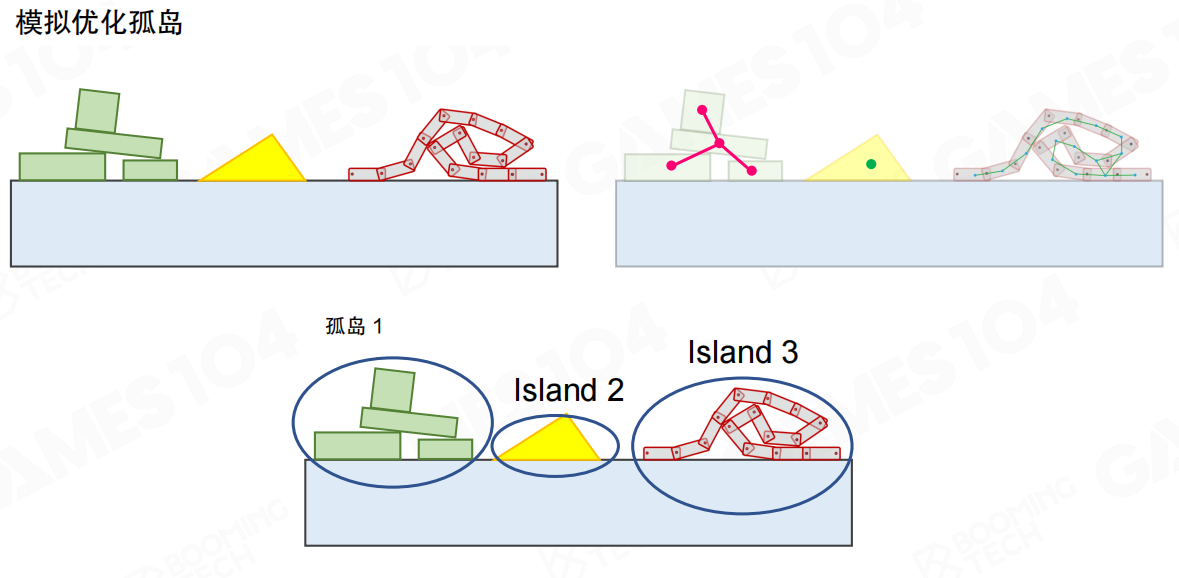
物理运算是十分消耗性能的，因此也需要类似渲染的加速处理，将对象划分为一组组孤岛。当孤岛没有受力变化时，整体处于稳定状态，这样就可以关闭孤岛的处理。

孤岛是指场景中相互接触或通过约束连接的一组物体。这些物体形成一个独立的物理系统，它们之间的相互作用不会影响其他孤岛。通过分析场景中的物体关系，我们可以将场景划分为多个孤岛，每个孤岛可以独立进行物理模拟。

当孤岛内没有外力作用时，整个孤岛处于稳定状态，所有物体都保持静止或匀速运动。此时，我们可以对孤岛进行休眠处理，停止对它的物理计算，从而节约计算资源。当孤岛受到外力作用时，再将其唤醒，重新开始物理模拟。

模拟优化：休眠（Hibernation）

休眠（Hibernation）是另一种重要的优化机制。模拟和求解所有刚体需要消耗大量资源，因此我们引入休眠机制。

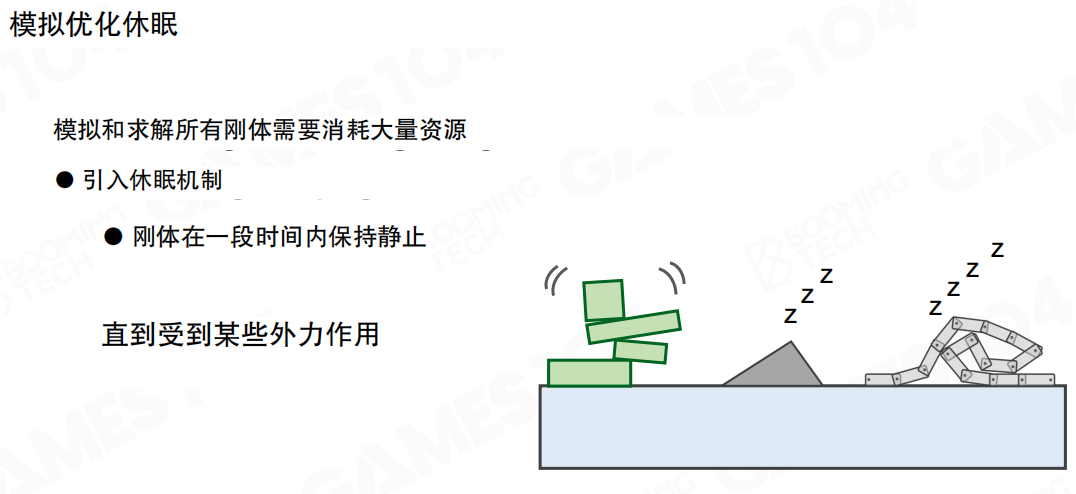
休眠机制的原理是：刚体在一段时间内保持静止，直到受到某些外力作用。当一个刚体在一段时间内没有运动或运动非常缓慢时，我们可以将其标记为休眠状态，停止对它的物理计算。

休眠的刚体不会参与碰撞检测、约束求解等计算，大大减少了计算量。当休眠的刚体受到外力作用时（比如被其他物体碰撞），它会自动唤醒，重新参与物理模拟。

休眠机制与孤岛优化结合使用，可以进一步提高物理系统的效率。一个完全静止的孤岛中的所有物体都可以进入休眠状态，直到有外力作用。

连续碰撞检测（Continuous Collision Detection，CCD）

游戏的运行并不是连续的，而是基于离散的时间步长。当物体的速度较大或者时间步长较长时，就可能出现”隧穿效应”（Tunneling Effect），即一个物体直接穿过另一个物体，而没有检测到碰撞。

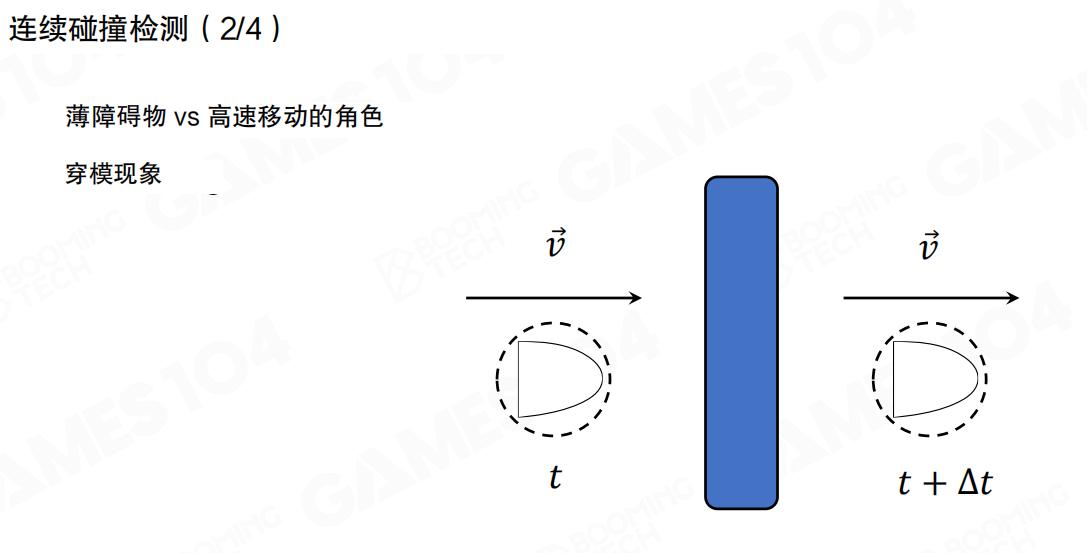
穿透现象（Penetration Phenomenon）是物理系统中的一个常见问题。当快速移动的物体遇到薄障碍物时，由于时间步长的离散性，物体可能在时间 t 时位于障碍物的一侧，在时间 t + Δt 时已经位于障碍物的另一侧，从而完全穿过了障碍物，而没有检测到碰撞。

处理这种问题最粗暴的方式就是增加检测对象的厚度，但这可能不符合美术要求。更好的方法是使用连续碰撞检测（Continuous Collision Detection，CCD）。

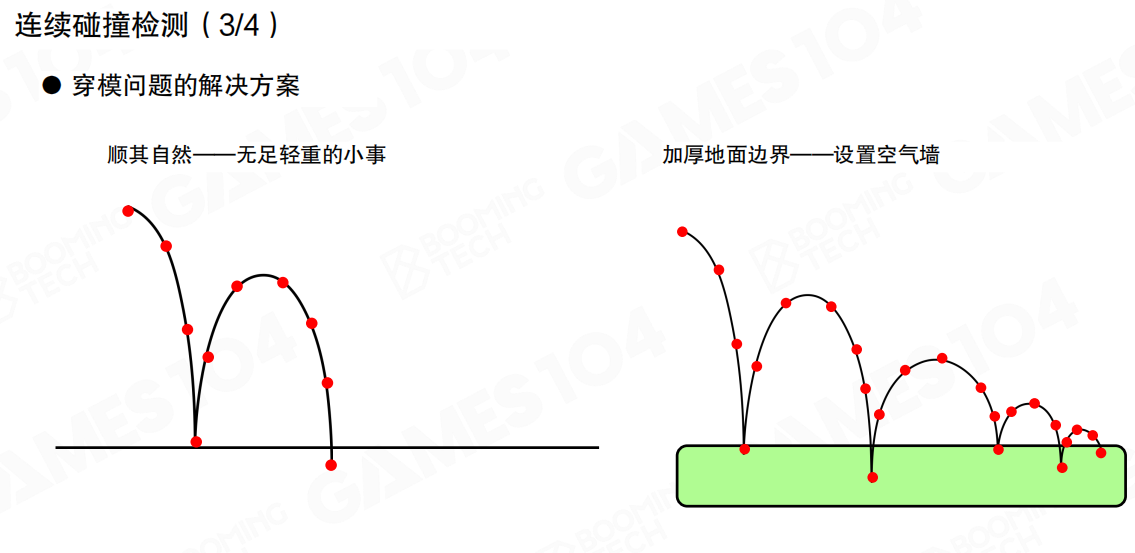
连续碰撞检测的解决方案有两种思路：

顺其自然——无足轻重的小事：允许轻微的穿透，这在某些情况下是可以接受的，比如物体穿透地面一点点，不会影响游戏体验。
加厚地面边界——设置空气墙：通过加厚碰撞边界或设置”空气墙”来防止穿透。这种方法虽然有效，但可能会影响游戏的手感和视觉效果。

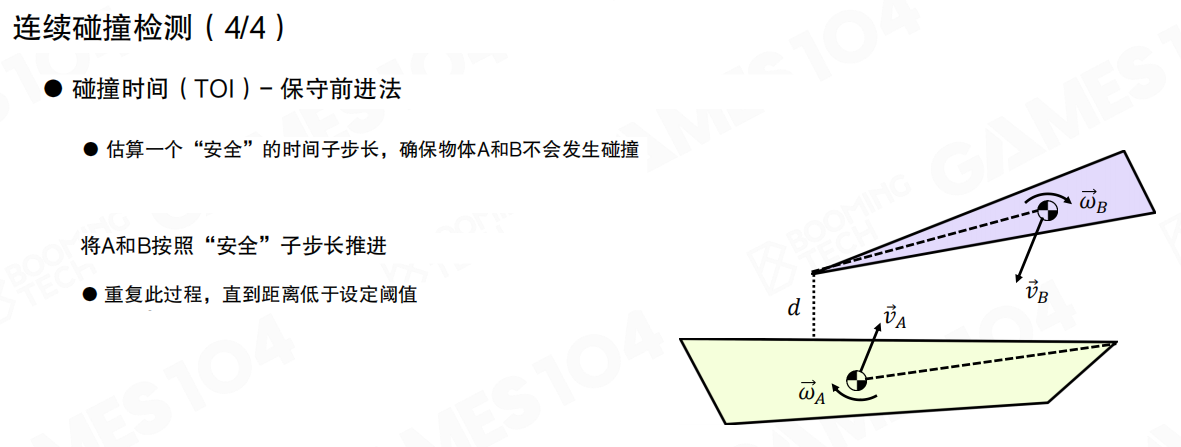
碰撞时间（TOI）- 保守前进法（Conservative Advancement Method）是一种更精确的连续碰撞检测方法：

估算一个”安全”的时间子步长：确保物体A和B不会发生碰撞
将A和B按照”安全”子步长推进：逐步移动物体，每一步都确保不会发生碰撞
重复此过程，直到距离低于设定阈值：当两个物体非常接近时，进行精确的碰撞检测

开启连续碰撞检测时，物体运动到特定范围内，增加物理碰撞的安全检测密度。连续碰撞检测的处理方式有很多种，Unity给出了基于扫描的连续碰撞检测（Sweep-based CCD）和推测性连续碰撞检测（Speculative CCD）。

确定性模拟（Deterministic Simulation）

对于物理世界的模拟存在一个重要的问题：如何保证相同的输入在不同设备上得到的结果一致？这在多人游戏中尤其重要。

确定性模拟（Deterministic Simulation）的需求主要来自：

对玩法产生物理影响的多人在线游戏：在多人游戏中，物理模拟的结果直接影响游戏玩法，如果不同玩家看到的结果不一致，会导致严重的游戏体验问题。
微小误差会引发蝴蝶效应：物理系统对初始条件非常敏感，微小的误差会随着时间推移而放大，导致完全不同的结果。
状态同步需要消耗带宽：如果每个客户端都独立进行物理模拟，需要同步大量的状态数据，消耗大量带宽。
同步输入需要确定性模拟：如果所有客户端使用相同的输入，应该得到相同的结果，这样就不需要同步物理状态，只需要同步输入即可。

非确定性模拟（Non-deterministic Simulation）的问题在于：尽管在编程时我们使用的都是同一套物理定律，在程序运行阶段由于帧率、计算顺序以及浮点数精度等问题，容易出现同一个场景在不同终端上产生不同的模拟结果。

确定性模拟的核心原则是：相同的旧状态 + 相同的输入 = 相同的新状态。

要实现确定性模拟，需要满足以下需求：

物理模拟的固定步长：使用固定的时间步长进行物理模拟，而不是依赖于帧率。即使帧率波动，物理模拟的时间步长也要保持一致。
确定性模拟求解序列：确保计算顺序是确定的，不会因为多线程或其他因素而改变。
浮点数一致性：使用相同的浮点数表示和运算规则，确保在不同平台上得到相同的结果。

影响计算结果的因素包括：

物理计算的目标帧率：需要设定固定的物理更新频率
迭代计算的步长和帧率：需要固定时间步长和迭代次数
浮点数的计算差异：不同平台、不同编译器可能产生不同的浮点数结果

确定性模拟是多人游戏物理系统的基础。通过确保所有客户端在相同输入下产生相同的结果，我们可以大大减少网络同步的开销，提高游戏的稳定性和一致性。

总结

效率、准确性与确定性是物理系统设计中的三个重要方面：

效率优化：
- 孤岛优化：将场景划分为独立的孤岛，对稳定的孤岛进行休眠处理
- 休眠机制：对静止的刚体进行休眠，减少不必要的计算
准确性提升：
- 连续碰撞检测：防止快速移动的物体穿透障碍物
- 保守前进法：通过安全时间步长逐步推进，确保碰撞检测的准确性
确定性保证：
- 固定时间步长：确保物理模拟的时间步长一致
- 确定性求解序列：确保计算顺序是确定的
- 浮点数一致性：确保不同平台上的计算结果一致

总而言之，物理仿真仍然是比较困难的。在现代游戏引擎中还有很多开放问题待我们进行解决。但通过合理的优化和设计，我们可以在效率、准确性和确定性之间找到平衡，构建出稳定、高效的物理系统。

转载请注明来源，欢迎对文章中的引用来源进行考证，欢迎指出任何有错误或不够清晰的表达。可以在下面评论区评论，也可以邮件至 785293209@qq.com