11.物理系统高级应用

游戏引擎 > 引擎体系 > 现代游戏引擎入门游戏引擎引擎体系现代游戏引擎入门

发布时间 : 2025-12-04 18:21

字数:21.1k 阅读 :

11.物理系统高级应用

11.物理系统高级应用

11.1 角色控制器

角色控制器（Character Controller）是玩家操作角色和游戏世界进行交互的接口。与很多人直观的认识不同，角色控制器在很多情况下实际上是非物理的。最常见的例子是玩家控制角色停止移动时角色会立即停住，而不是严格按照刚体仿真那样通过摩擦力来逐渐停止运动。某种意义上讲，角色控制器虽然是反物理的，但却更符合人对物理世界的认知。

在传统的游戏开发中，角色控制往往依赖于大量精心调整的数值来带来良好的操作手感。这些数值的调整需要大量的经验和反复测试，形成了行业遗留代码。现代游戏引擎通过角色控制器系统，将这些复杂的逻辑封装起来，为开发者提供了更便捷的接口。

在物理系统中构建控制器

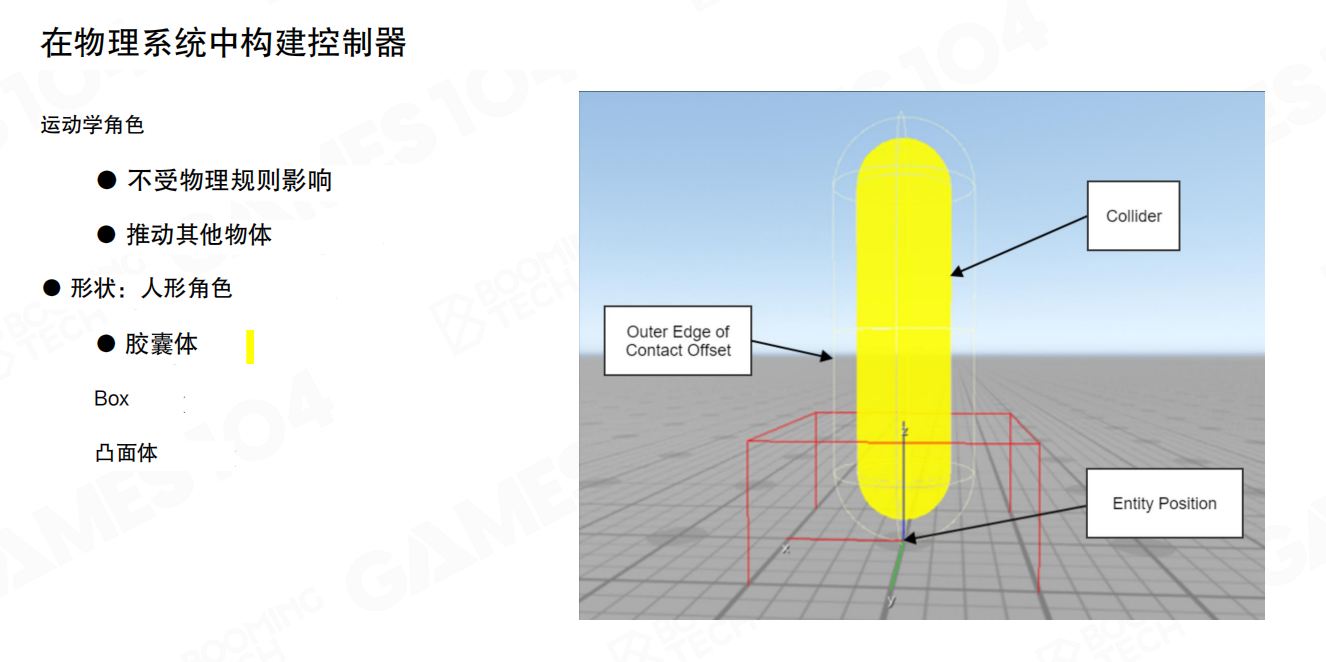
在构建角色控制器时，一般会使用简化后的形状来包裹角色，这样便于处理各种场景之间的互动。

运动学角色（Kinematic Character）的特性：

不受物理规则影响：角色不会受到重力、摩擦力等物理力的影响
推动其他物体：角色可以推动场景中的动态物体

形状：人形角色（Shape: Humanoid Character）：

胶囊体（Capsule）：最常用的人形角色形状，由一个圆柱体和两个半球体组成
Box：长方体形状，适用于某些特殊需求
凸面体（Convex Mesh）：更复杂的形状，但计算成本更高

控制器使用接触偏移（Contact Offset）来扩展碰撞检测范围，确保在角色移动时能够提前检测到碰撞，避免穿透问题。

与环境碰撞

在角色和场景进行互动时，最常见的情况是玩家控制的角色撞到了墙壁上。如果严格按照物理引擎进行模拟，此时角色会一直停在碰撞的位置；而现代游戏中更常见的处理方式是修改角色的运动方向，使得角色可以沿墙壁方向进行滑动。

与环境碰撞检测（Collision with Environment）的处理流程：

扫描测试（Scan test）：使用扫描测试检测角色移动路径上的碰撞
自动沿墙滑动（Automatic sliding along wall）：
- 计算切线方向：当角色碰撞到墙壁时，计算墙壁的切线方向
- 沿切线方向移动：将角色的运动方向调整为沿墙壁的切线方向，实现平滑的滑动效果

这种处理方式避免了角色卡在墙角的问题，提供了更流畅的游戏体验。如果不进行这种处理，角色在碰撞到墙壁后会立即停止，玩家会感觉操作非常僵硬。

角色控制器的特性

角色控制器（Character Controller）并非基于物理，角色假设摩擦力无穷大，且没有弹性。这意味着：

可控刚体交互：角色控制器可以精确控制角色的运动，不受物理引擎的惯性影响
近似无限摩擦力/无弹性恢复：角色可以立即停止，不会因为惯性继续滑动
加速与刹车几乎瞬间改变方向并实现瞬移：角色可以快速响应玩家输入，实现精确的控制

与动态演员（Dynamic Actor）不同，角色控制器不受物理规则影响，但可以推动其他物体。动态演员则完全遵循物理规则，会受到重力、摩擦力、弹性等物理因素的影响。

坡度限制与滑坡受力

对于斜坡这种情况，如果按照刚体运动学进行处理会导致角色下坡时直接从斜坡上滑下来，或是在上坡时由于具有过大的速度角色直接冲上它不应该到达的位置。为了避免这些问题，需要单独考虑角色停在斜坡或是限制角色的位置。

坡度限制与滑坡受力（Slope Limit and Sliding Force）的处理：

最大爬坡角度（Maximum Climbing Angle）：设置角色能够爬上的最大坡度。如果坡度超过这个角度，角色将无法爬上
在陡坡上滑行（Sliding on a Steep Slope）：当角色站在超过最大爬坡角度的斜坡上时，角色会沿着斜坡向下滑动

通过合理设置最大爬坡角度，可以控制角色能够到达的区域，避免角色爬上不应该到达的位置。同时，在陡坡上的滑行效果也增加了游戏的真实感。

自动步进及其问题

上下楼梯同样也是角色在场景中的一种常见行为。如果严格按照物理仿真进行处理，胶囊的上下楼梯会非常地困难。因此在游戏引擎中需要单独考虑这种情况，当角色上下楼梯时自动修正角色的位置。

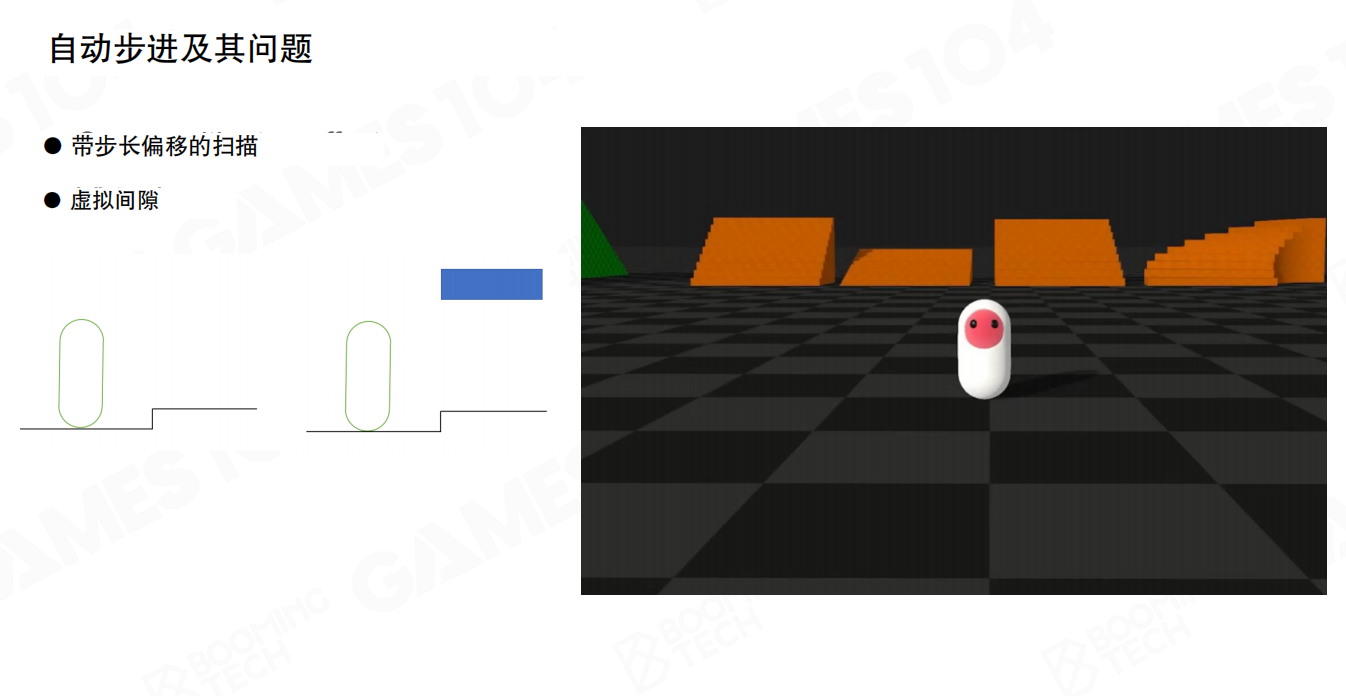
自动步进（Auto Stepping）的处理方式：

带步长偏移的扫描（Scan with step length offset）：在角色移动时，使用带步长偏移的扫描测试来检测前方是否有台阶
虚拟间隙（Virtual Gap）：在台阶和角色之间创建一个虚拟间隙，允许角色自动跨过一定高度的台阶

自动步进功能使得角色可以平滑地上下楼梯，而不需要玩家精确控制每一步。这对于提升游戏体验非常重要，特别是在需要频繁上下楼梯的场景中。

控制器体积更新

角色控制器还需要考虑角色体积发生变化的情况。当玩家控制角色进行下蹲等动作时需要自动更新角色控制体的体积，否则容易出现角色卡在门口无法进入的问题。

控制器体积更新（Controller Volume Update）的处理：

在运行时动态调整控制器体积大小：例如下蹲动作时，需要减小控制器的高度和宽度
更新前进行重叠测试：在更新控制器体积之前，先进行重叠测试，避免插入物体内部

在更新控制器体积时，需要确保新的体积不会与场景中的其他物体发生重叠。如果直接更新体积而不进行检测，角色可能会被卡在物体内部，导致无法移动。

控制器推动物体

当玩家控制角色和场景中的物体互动时，需要对动态对象的运动状态加以更新。比较常见的处理方式是发生碰撞时对动态对象施加一个相应的冲量来控制它们的运动。

控制器推动物体（Controller Push Objects）的处理：

当角色控制器与动态Actor发生碰撞时触发命中回调：检测到碰撞后，触发相应的回调函数
对动态角色施加力：根据碰撞信息，对动态物体施加相应的力或冲量，使其产生运动

这种处理方式使得角色可以推动场景中的箱子、桶等动态物体，增加了游戏的互动性。通过合理设置施加的力的大小，可以控制推动物体的难易程度，影响游戏的手感。

站在移动平台上

除此之外，角色控制器还需要考虑动态场景的情况。当角色位于运动的平台时需要根据平台的运动来调整角色的运动状态，否则会出现平台发生运动时角色的运动没有同步或是滞后的问题。

站在移动平台上（Standing on a Moving Platform）的处理：

角色需要跟踪所在平台的运动，并将平台的运动叠加到角色的运动上。这样，当平台移动时，角色会跟随平台一起移动，而不会出现角色停留在原地或滞后的问题。

这种处理在电梯、移动平台等场景中非常重要。如果角色不能正确跟随平台运动，玩家会感觉角色”飘”在平台上，或者从平台上掉下来，严重影响游戏体验。

总结

角色控制器是游戏引擎中一个非常重要的系统，它通过一系列精心设计的”hack”来实现符合玩家预期的角色控制效果：

非物理特性：角色控制器不受物理规则影响，可以实现精确的控制
环境交互：通过沿墙滑动、自动步进等功能，实现流畅的环境交互
动态调整：支持体积更新、推动物体、跟随平台等动态场景处理

虽然角色控制器在某种程度上是”反物理”的，但它更符合玩家对游戏世界的认知和期望，是游戏开发中不可或缺的重要组件。

11.2 布娃娃系统

布娃娃（Ragdoll）系统是游戏角色动画的一个重要组成部分，它最常见的例子是角色的处决动画：当玩家控制的角色处决了某个游戏对象时，根据处决场景的不同被处决对象会发生相应场景互动的动作。

为什么我们应该使用布娃娃系统？传统的角色动画是预先录制的，角色在死亡时会简单地”倒地而亡”，动作僵硬且缺乏真实感。而在”命悬一线”的紧张场景中，角色需要根据物理环境做出自然的反应。通过启用物理引擎，布娃娃系统可以让角色在受到外力时产生真实的物理反应，大大提升了游戏的代入感和真实感。

将骨骼映射到刚体

实际上，布娃娃系统与前面介绍过的骨骼动画密切相关。在模拟布娃娃的运动时，我们同样会在角色身上设置相应的节点，并把不同节点之间的骨骼按照刚体进行模拟。不过出于实时计算上的考虑，布娃娃一般只会使用非常少量的节点和骨骼来进行模拟。

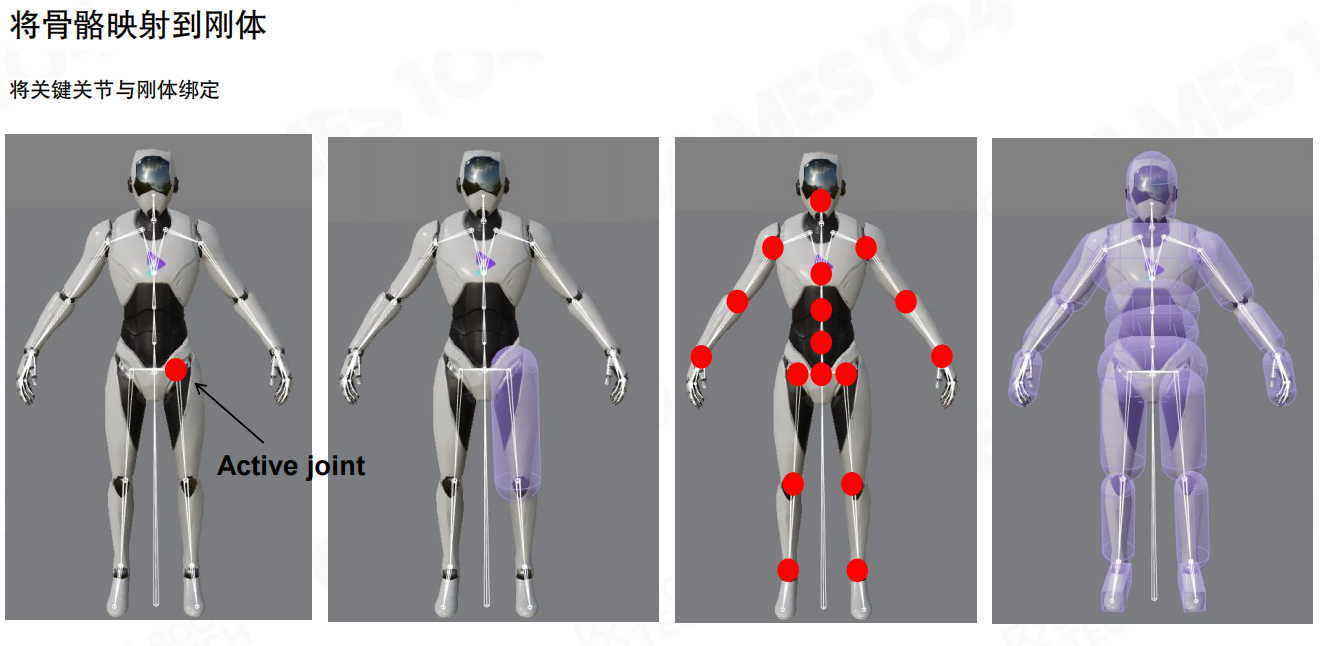
将骨骼映射到刚体（Map Skeleton to Rigid Bodies）的过程包括：

将关键关节与刚体绑定：首先需要识别角色骨骼中的关键关节，如头部、肩膀、肘部、手腕、髋部、膝盖、脚踝等
为每个关键关节创建刚体：为每个关键关节创建一个刚体，通常使用胶囊体或球体来近似表示
连接刚体：使用约束将相邻的刚体连接起来，形成完整的物理骨架
调整刚体大小：确保刚体尽可能贴合角色的网格，以获得准确的物理模拟

通过这个过程，角色的骨骼结构被映射到物理引擎的刚体系统中，使得角色可以接受物理力的作用。

人体关节约束

同样地，在布娃娃中需要考虑角色身上不同节点的运动是带有一定约束的。如果忽略了人体骨骼关节的约束，则会导致非常扭曲的模拟效果。

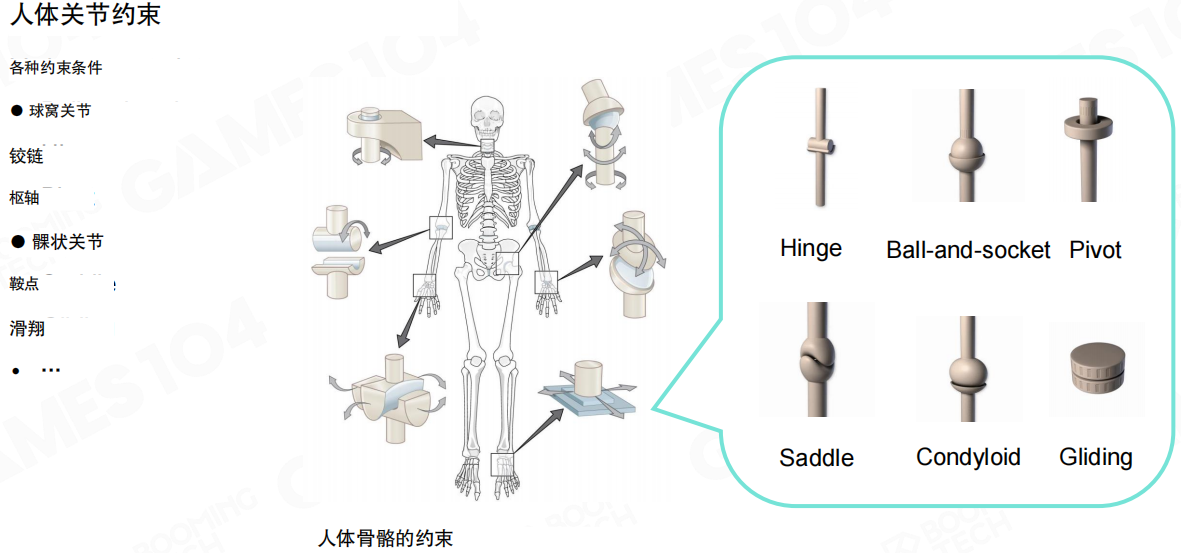
人体关节约束（Human Joint Constraints）包括多种类型：

球窝关节（Ball-and-socket）：如肩关节和髋关节，允许多方向的旋转
铰链（Hinge）：如肘关节和膝关节，只允许在一个平面内弯曲
枢轴（Pivot）：如颈椎，允许围绕一个轴旋转
髁状关节（Condyloid）：如腕关节，允许在两个平面内运动
鞍点（Saddle）：如拇指的腕掌关节，允许在两个平面内运动
滑翔（Gliding）：如腕骨之间的关节，允许有限的滑动

约束条件应与解剖学骨骼结构相匹配，这样才能产生真实的物理反应。

关节约束的重要性（The Importance of Joint Constraints）可以通过对比看出：

正确约束下的结果：角色能够自然地站立在地面上，关节运动符合人体解剖学结构，产生真实的物理反应
仅自由铰链出现异常结果：如果关节没有正确的约束，角色可能会浮在空中，或者产生扭曲、不自然的姿态

这说明正确的关节约束对于布娃娃系统的真实性至关重要。

约束条件的属性

约束条件需要仔细调整，不同的设置会产生不同的效果。

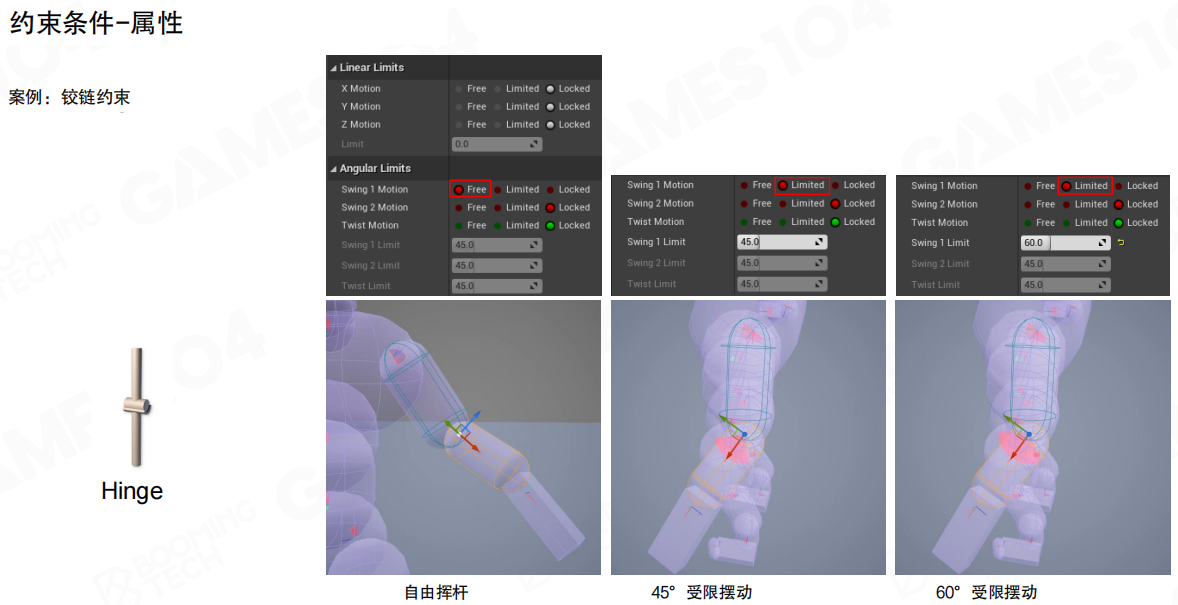
以铰链约束（Hinge Constraint）为例，可以通过调整以下属性来控制关节的运动：

线性限制（Linear Limits）：控制关节在X、Y、Z轴上的线性运动，可以设置为自由（Free）、锁定（Locked）或受限（Limited）
角度限制（Angular Limits）：
- Swing 1 Motion 和 Swing 2 Motion：控制关节在两个摆动方向上的运动
- Twist Motion：控制关节的扭转运动
- Limit：设置运动的角度限制

通过调整这些参数，可以实现：

自由挥杆（Free Swing）：关节可以自由摆动，没有角度限制
45°受限摆动（45° Limited Swing）：关节的摆动被限制在45度范围内
60°受限摆动（60° Limited Swing）：关节的摆动被限制在60度范围内

不同的限制设置会产生不同的物理反应，需要根据实际需求进行调整。

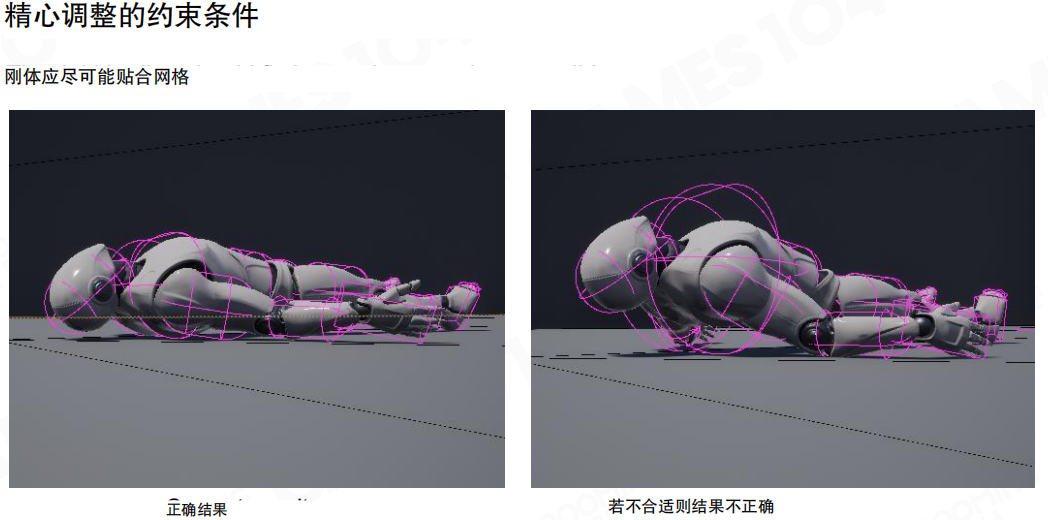
精心调整的约束条件（Carefully adjusted constraint conditions）非常重要：

刚体应尽可能贴合网格：刚体的形状和大小应该尽可能贴合角色的网格，这样才能获得准确的碰撞检测和物理模拟
正确结果：当约束条件设置正确时，角色在物理模拟中会表现出自然的姿态，刚体紧密贴合角色的网格
若不合适则结果不正确：如果约束条件设置不当，刚体可能会过大或过小，导致角色在物理模拟中出现不自然的姿态，甚至出现穿透或分离的问题

一般来说，布娃娃关节的约束会由技术美术（TA）进行设置，如果设置得不好会出现一些反直觉的动画效果。

通过布娃娃系统驱动骨骼动画

需要注意的是，尽管我们可以使用布娃娃来模拟角色的动画，在实际游戏中仍然是需要通过骨骼关节系统来驱动整个角色的运动。由于布娃娃中的骨骼关节数量一般会少于实际角色的骨骼关节，我们需要使用动画重定向技术来将布娃娃计算出的运动映射到实际的角色骨骼上。

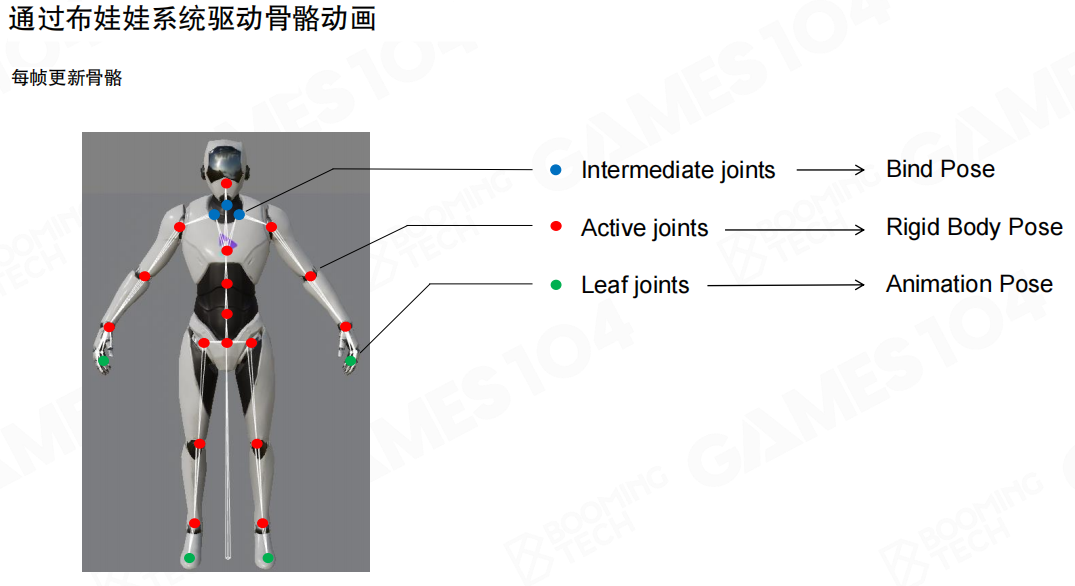
通过布娃娃系统驱动骨骼动画（Driving skeletal animation through a ragdoll system）需要每帧更新骨骼：

中间关节（Intermediate joints）：这些关节使用绑定姿态（Bind Pose），保持原始骨骼的初始状态
活动关节（Active joints）：这些关节使用刚体姿态（Rigid Body Pose），由物理引擎计算得出
叶子关节（Leaf joints）：这些关节使用动画姿态（Animation Pose），通常由动画系统驱动

通过这种方式，布娃娃系统可以驱动角色的骨骼动画，同时保持动画系统的完整性。

动画与布娃娃效果的融合

在使用时还需要注意角色动画切换到布娃娃的过程。还是以角色处决动画为例，在一开始被处决对象是使用预先录制的角色动画，然后在某一时刻会切换成布娃娃使用物理系统来实时计算角色的行为。

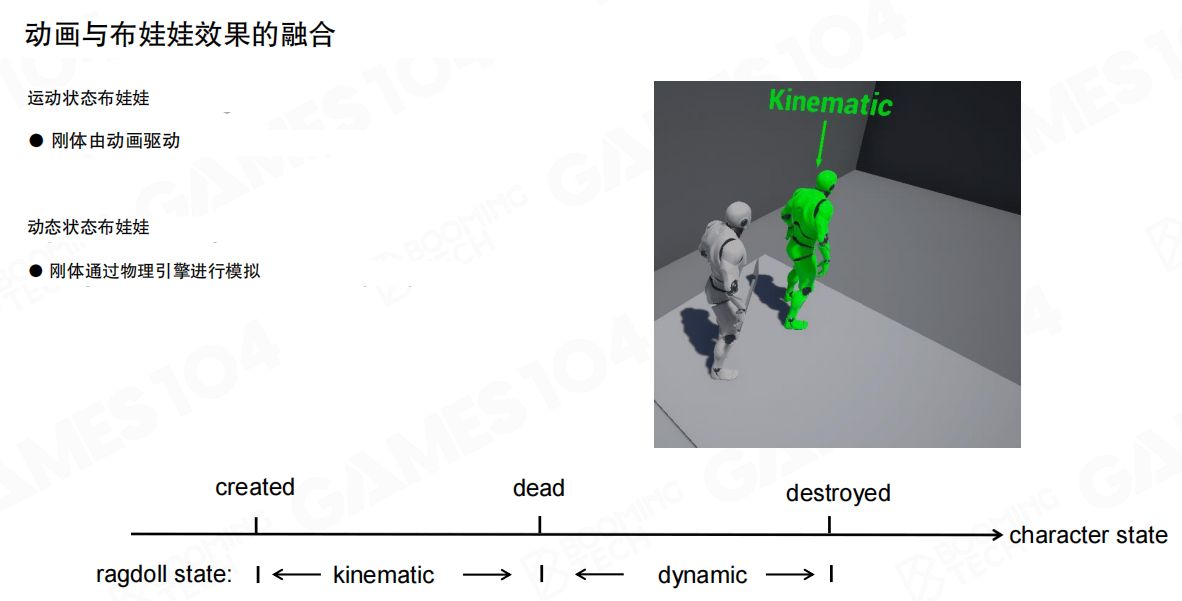
动画与布娃娃效果的融合（Integration of Animation and Ragdoll Effects）包括两种状态：

运动状态布娃娃（Kinematic Ragdoll）：
- 刚体由动画驱动：角色的刚体完全由动画系统控制，不受物理力的影响
- 这种状态通常用于角色还活着的时候，确保角色按照预定义的动画运动
动态状态布娃娃（Dynamic Ragdoll）：
- 刚体通过物理引擎进行模拟：角色的刚体完全由物理引擎控制，会受到重力、碰撞等物理力的影响
- 这种状态通常用于角色死亡后，让角色产生真实的物理反应

在角色的生命周期中，布娃娃状态会从运动状态（kinematic）转换到动态状态（dynamic），通常在角色死亡时进行转换。

更进一步，在现代3A游戏中还会将角色动画和布娃娃实时计算出的动画进行混合来提升玩家的代入感和游戏体验。

布娃娃物理系统 - 物理与动画融合（Ragdoll Physics System - Physics and Animation Blending）通过在动画姿态与物理姿态之间进行混合来实现：

混合流程：

动画（Animation）：提供预定义的动画姿态
控制/IK（Controls/IK）：通过反向运动学调整动画姿态
物理（Physics）：物理引擎计算出的物理姿态
混合（Blend）：根据物理权重（PhysicsWeight）参数，在动画姿态和物理姿态之间进行混合

通过调整物理权重，可以实现三种不同的效果：

动画（Animation）：完全使用预定义的动画，角色姿态固定，缺乏真实感
仅布娃娃物理（Only Ragdoll Physics）：完全使用物理模拟，角色完全受物理力影响，可能产生过于夸张的姿态
物理动画融合（Physics Animation Blending）：将动画和物理模拟进行混合，既保持了动画的流畅性，又增加了物理的真实感

这种混合方式在现代游戏中非常常见，可以创造出既流畅又真实的角色动画效果。

总结

布娃娃系统是游戏引擎中一个非常重要的物理模拟系统，它通过以下方式实现了真实的角色物理反应：

骨骼映射：将角色的骨骼结构映射到物理引擎的刚体系统
关节约束：通过设置正确的关节约束，确保角色运动符合人体解剖学结构
动画驱动：通过动画重定向技术，将布娃娃的运动映射到完整的骨骼系统
状态转换：在运动状态和动态状态之间进行转换，实现从动画到物理的平滑过渡
动画融合：将预定义的动画和物理模拟进行混合，创造出既流畅又真实的动画效果

布娃娃系统大大提升了游戏的真实感和代入感，是现代游戏开发中不可或缺的重要技术。

11.3 衣料模拟

布料系统（Cloth System）是游戏物理仿真中的重要一环。衣料模拟的质量直接影响角色的真实感和游戏体验。一个角色是否”活”起来，除了表情和头发，衣料的灵动性也是关键因素。当角色回眸一笑，衣料随风飘动，那种微妙的细节会让角色显得更加生动可爱。

基于动画的布料模拟

早期的布料模拟是使用预先录制的动画来实现的。我们可以在角色身上设置一些额外的骨骼来控制衣物的运动，这样就可以实现角色执行不同动作时衣物随之飘动的效果。

基于动画的布料模拟（Animation-based Cloth Simulation）的渲染管线包括：

动画师负责制作骨骼动画：动画师在DCC工具中为角色制作骨骼动画，包括控制衣料的额外骨骼
通过DCC工具生成更多动画数据：在DCC工具中生成更多的动画数据，包括衣料的飘动动画
引擎在运行时重新播放动画：游戏引擎在运行时重新播放这些预制的动画，实现衣料的运动效果

优点：

廉价（Inexpensive）：计算成本低，不需要物理引擎参与
可控性（Controllability）：动画师可以精确控制衣料的运动，确保视觉效果符合预期

缺点：

不切实际（Impractical）：衣料运动是预制的，无法根据实际情况动态调整
无法与环境互动（Cannot interact with the environment）：衣料无法与环境中的物体产生真实的物理交互
服装的命名受到限制（Naming of clothing is restricted）：只能表现预设的动画效果，灵活性有限

这种方法在手机游戏中很受欢迎，因为移动设备的计算资源有限，使用动画方法可以在保证视觉效果的同时降低计算成本。

基于刚体的布料模拟

另一种处理衣物的方法是使用刚体运动的方法来模拟衣物和角色以及场景的互动。这样的处理方法虽然需要更多的计算资源，但可以实现相对真实衣物运动的效果。

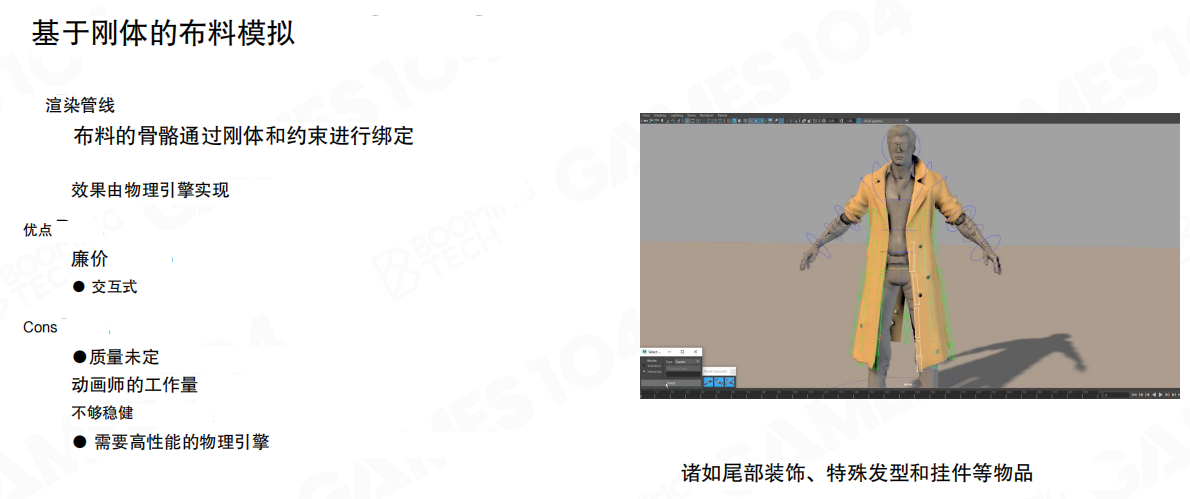
基于刚体的布料模拟（Rigid Body Cloth Simulation）的渲染管线包括：

布料的骨骼通过刚体和约束进行绑定：将布料的骨骼通过刚体和约束绑定到物理系统中
效果由物理引擎实现：衣料的运动效果完全由物理引擎计算得出

优点：

廉价（Cheap）：相比基于网格的模拟，计算成本较低
交互式（Interactive）：可以实现衣料与环境、角色的真实物理交互

缺点：

质量未定（Quality uncertain）：模拟质量取决于刚体的数量和约束的设置
动画师的工作量（Animator’s workload）：需要动画师手动设置大量的刚体和约束
不够稳健（Not robust enough）：在某些情况下可能出现不稳定的模拟效果
需要高性能的物理引擎（Requires a high-performance physics engine）：需要物理引擎支持刚体和约束的计算

这种方法适用于诸如尾部装饰、特殊发型和挂件等物品的模拟。在早期的PC游戏中，这种方法也非常常见，因为那时已经有了基础的物理计算能力，但又舍不得使用更昂贵的基于网格的布料模拟。

基于网格的布料模拟

在现代游戏引擎中，衣物运动更多地是使用网格来进行模拟。这是现在游戏引擎发展的主流趋势，几乎所有动态的衣料都是用网格的方法，一个顶点一个点地做物理学的计算。

渲染网格和物理网格（Render Mesh and Physical Mesh）的区别：

渲染网格（Render Mesh）：用于视觉渲染的网格，通常非常细腻，包含大量的顶点和面，用于呈现高质量的视觉效果
物理网格（Physical Mesh）：用于物理模拟的网格，密度比渲染网格稀疏很多，通常只有渲染网格的1/4到1/10，甚至更少

出于计算效率上的考虑，布料仿真中使用的网格要比渲染中的网格稀疏很多。例如，如果渲染网格有4000个面，物理网格可能只有400到500个面。这是因为物理模拟需要实时计算，而渲染网格的顶点数量太多会导致物理引擎无法实时处理。

通过顶点动画插值（Vertex Animation Interpolation）技术，可以将物理网格的运动插值到渲染网格的其他顶点上，这样既保证了物理模拟的效率，又保持了视觉效果的细腻。

布料约束

在布料仿真中，往往还会为网格上的每个顶点赋予一定位移的约束，从而获得更符合人直觉的仿真结果。

布料绘制模拟约束（Cloth Drawing Simulation Constraints）的处理方式：

为每个顶点添加最大半径约束（Add maximum radius constraint for each vertex）：为物理网格上的每个顶点设置一个最大移动半径，限制顶点的移动范围

这种约束非常重要，因为很少有衣料真的是飘在空中的，大部分衣料都是穿在人的身上。如果不对顶点进行约束，衣料在模拟时可能会飞走，导致角色”裸奔”。

约束权重的设置：

靠近身体的地方：约束权重较高，限制顶点的移动范围，防止衣料与角色穿模
远离身体的地方：约束权重较低，允许更大的移动范围，实现自然的飘动效果

例如，在做披风时，沿着脖子的这一圈会设置约束权重为零，让披风固定在脖子上。越往下，约束权重越小，允许披风有更大的飘动空间。

布料物理材质

作为美术师，可以设置很多参数来控制布料的物理行为，比如布料的硬度、切向的韧劲、抗弯曲能力等。

设置布料物理材质（Set Cloth Physical Material）的参数包括：

重力缩放（Gravity Scale）：控制布料受重力影响的程度
摩擦力（Friction）：布料表面的摩擦系数
弯曲阻力（Bend Resistance）：抵抗弯曲的能力
剪切阻力（Shear Resistance）：抵抗剪切变形的能力
拉伸限制（Stretch Limit）：允许的最大拉伸程度
松弛（Relax）：布料的松弛程度
阻尼（Damping）：运动的阻尼系数
拖拽（Drag）：空气阻力系数
惯性混合（Inertia Blend）：惯性的混合比例

纤维限制（Fiber Limits）：

压缩（Compression）：允许的最大压缩程度
扩张（Expansion）：允许的最大扩张程度
阻力（Resistance）：纤维的阻力系数

通过调整这些参数，可以创造出各种不同质感的衣料，比如丝绸质感、皮革质感等。当然，还需要结合渲染部分的内容，才能让衣料看起来更加真实。

质量弹簧系统

使用网格进行布料仿真的基本处理方法是使用质量弹簧系统（Mass-Spring System）进行模拟。我们为网格的顶点赋予一定的质量，然后将相邻顶点使用弹簧连接起来，就形成了布料仿真的物理系统。

布料求解器——质量弹簧系统（Cloth Solver — Mass-Spring System）：

弹簧力（Spring Force）：
[
\vec{F^S} = k_{spring} \cdot \Delta\vec{x}
]

其中，(k_{spring})是弹簧系数，(\Delta\vec{x})是弹簧的位移向量。

弹簧阻尼力（Spring Damping Force）：
[
\vec{F^D} = -k_{damping} \cdot \vec{v}
]

其中，(k_{damping})是阻尼系数，(\vec{v})是速度向量。

阻尼力非常重要，因为如果没有阻尼，弹簧会永远做简谐振动，无法停下来。阻尼力将机械能转化为热能，让系统最终能够稳定下来。

在构建弹簧系统时，除了在横竖方向上设置弹簧外，一般还需要在对角方向上设置一些弹簧，这样可以保证布料具有抵抗对角方向的刚度。

弹簧类型：

结构弹簧（Structural Springs）：连接横向和纵向相邻的顶点，形成基本的网格结构
剪切弹簧（Shear Springs）：连接对角方向的顶点，抵抗剪切变形
弯曲弹簧（Bending Springs）：连接跨越多行的顶点，抵抗弯曲变形

如果没有剪切弹簧和弯曲弹簧，布料会显得特别软，缺乏真实感。但对于某些布料，比如丝绸，这种柔软的感觉反而更符合实际。

对于一个顶点，我们可以对其施加力的分析。完整的力方程包括：

[
\vec{F}{net}^{vertex}(t) = M \cdot \vec{g} + \vec{F}{wind}(t) + \vec{F}{air\ resistance}(t) + \sum{Springs \in v} (k_{spring} \cdot \Delta\vec{x}(t) - k_{damping} \cdot \vec{v}(t)) = M \cdot \vec{a}(t)
]

其中：

(M \cdot \vec{g})：重力
(\vec{F}_{wind}(t))：风力
(\vec{F}_{air\ resistance}(t))：空气阻力
(\sum_{Springs \in v})：所有连接弹簧的力的总和

接下来，我们只需使用积分器计算下一位置。在布料模拟中，韦尔莱算法（Verlet Algorithm）是个不错的选择。

Verlet积分公式：
[
\vec{x}(t + \Delta t) = 2 \cdot \vec{x}(t) - \vec{x}(t - \Delta t) + \vec{a}(t) \cdot (\Delta t)^2
]

Verlet积分法

对质点弹簧系统进行仿真时，不可避免地会使用到一些数值积分的方法。Verlet积分（Verlet Integration）本质仍然是半隐式欧拉积分，不过在实际积分时可以将速度项约掉，只保留位移和加速度项就能进行计算。

Verlet积分法——回顾半欧拉法（Verlet Integration Method — Review of Semi-implicit Euler Method）：

半隐式欧拉法（Semi-implicit Euler Method）：
[
\vec{v}(t + \Delta t) = \vec{v}(t) + \vec{a}(t) \Delta t
]
[
\vec{x}(t + \Delta t) = \vec{x}(t) + \vec{v}(t + \Delta t) \Delta t
]

Verlet积分法的推导：

从半隐式欧拉法出发，我们可以推导出Verlet积分法：

当前速度可以表示为：
[
\vec{x}(t) = \vec{x}(t - \Delta t) + \vec{v}(t)\Delta t
]
将速度表达式代入位置更新公式，整理后得到：
[
\vec{x}(t + \Delta t) = 2\vec{x}(t) - \vec{x}(t - \Delta t) + \vec{a}(t)(\Delta t)^2
]

Verlet积分法在计算时无需考虑速度，因此速度更快。这是因为：

不需要存储速度：只需要存储当前位置和上一帧的位置，就可以计算下一帧的位置
数值稳定性更好：避免了速度项可能带来的数值不稳定问题
计算效率更高：减少了需要存储和计算的数据量

虽然从数学上看，Verlet积分和半隐式欧拉积分是等价的，但Verlet积分在实际应用中更加稳定和高效，因此在布料模拟中被广泛使用。

基于位置的动力学

更进一步，现代游戏引擎中越来越多的布料模拟使用的其实不是简单的速度加速度方法，而是使用基于位置的动力学（Position-Based Dynamics, PBD）的思想。

布料求解器——基于位置的动力学（Cloth Solver — Position-Based Dynamics）：

基本上，模拟需要约束力（Constraint Force）、速度（Velocity）和位置（Position）。幸运的是，我们有基于位置的动力学（PBD）约束，它可以直接约束位置。

PBD的核心思想：

传统的经典力学方法是：根据约束算出力 → 根据力算出速度 → 根据速度算出位移。这是一个非常合理的因果关系。

而PBD使用的是拉格朗日数学的思想，它把所有的力学关系描述成数学约束，认为所有的力学过程必须要符合数学约束。PBD直接用约束直接解除位置，而不再关心速度。

PBD的优点：

能处理非常复杂的情况：可以处理多约束、非线性约束等复杂情况
求解器非常稳定：在精度敏感的情况下也能保持稳定
计算速度较快：相比传统方法，PBD的计算效率更高

例如，一条几万个面的龙，用一块布料从头上划过去，这个案例非常复杂，但PBD可以很好地处理这种情况。

自碰撞

布料仿真的一大难点在于如何处理自相交（Self-collision）问题。由于我们使用了没有体积的网格来表示布料，在进行仿真时很容易出现网格直接相互的穿插。

自碰撞（Self-collision）：

作为一种柔性材质，布料能够自我折叠并与自身发生碰撞：布料可以折叠，不同部分之间会发生碰撞
这在实时游戏物理模拟中相当棘手：自碰撞检测和解决是实时物理模拟中的一个重大挑战

当布料的两面使用不同的颜色时，如果关闭自碰撞检测，布料之间就会互相穿插，导致视觉效果非常糟糕。即使两边的颜色一样，当布料动起来的时候，两个布料在一起也会经常”打架”，特别是在角色身上。

现在在表达一个角色的时候，衣服都要穿好几层，每一层布料都在做自我的模拟。当这么多层布料在一起模拟的时候，如果发生穿插，比如里面的T恤（蓝色）穿透出来，出现在外面的外套（白色）上面，玩家一看就会觉得游戏质量不行。

自碰撞的常见解决方案：

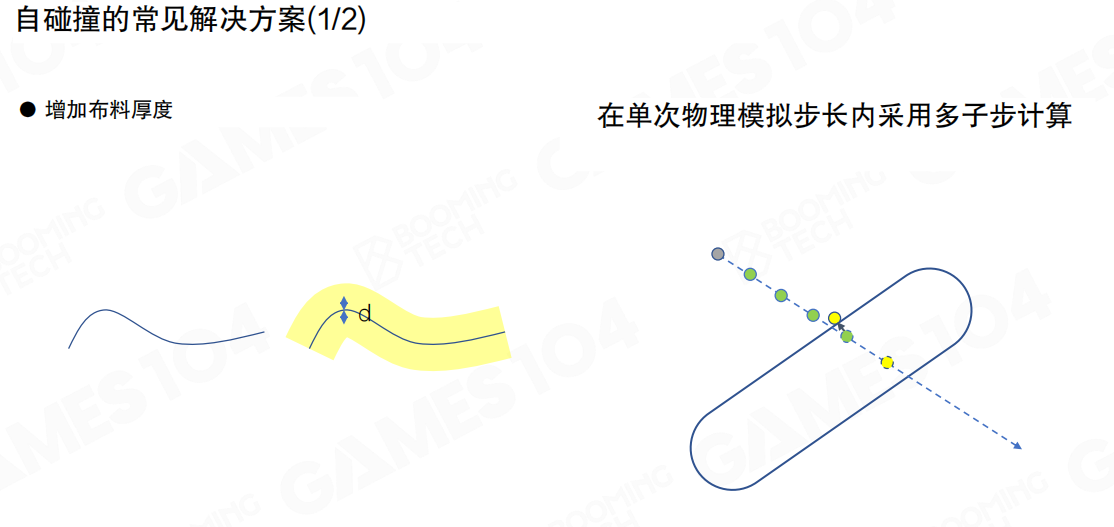
增加布料厚度（Increase Cloth Thickness）：

把布料的物理模拟模型加厚，虽然还是会穿过去，但只要穿得不够深，就不会透出来
这是一个比较简单但有效的方法

在单次物理模拟步长内采用多子步计算（Using Multiple Sub-steps within a Single Physics Simulation Step）：

把物理仿真的步长变得更细，拆成很多子步（sub-step）
这样在求解时，可以保证不会过深地穿透布料
这是用计算复杂度来换稳定性的方法

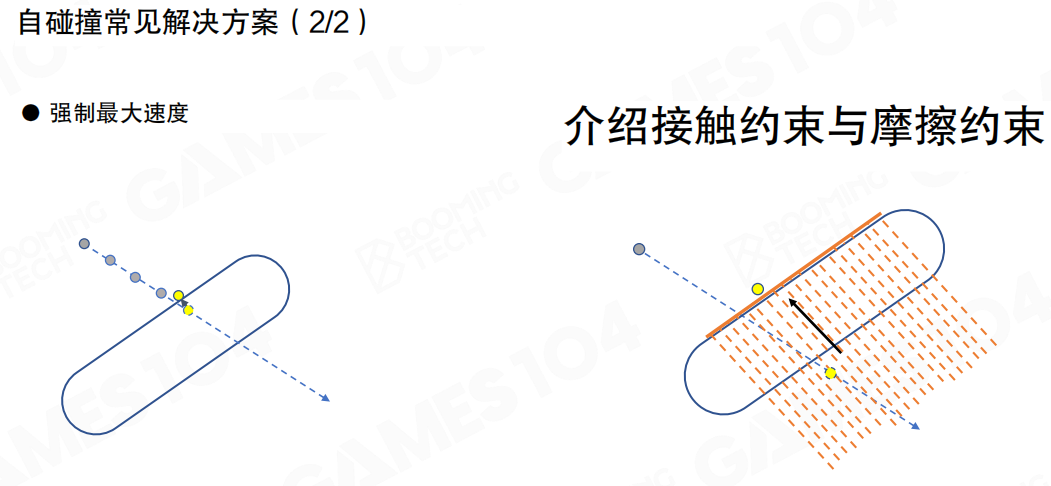
强制最大速度（Enforce Maximum Speed）：

设置一个最大速度限制，保证在每个子步上，不会把布料穿得过深
这样即使发生穿透，也能弹回来
这是因为在布料模拟时，速度项可能不稳定，导致穿透后无法恢复

介绍接触约束与摩擦约束（Introduction to Contact Constraints and Friction Constraints）：

更精确的做法：加一个力场，这个力场一般会设置在布料的里面
当布料穿过去之后，力场能检测出来，产生一个反向的冲量，把布料往回顶
这相当于在布料里面建了一层有符号距离场（SDF, Signed Distance Field）
当有布料穿到里面去之后，SDF就会起作用，产生反向的冲量把它顶出来

总结

布料模拟是游戏引擎中一个非常重要且复杂的系统。它通过以下方式实现了真实的衣料物理反应：

多种模拟方法：从简单的动画方法到基于刚体的方法，再到基于网格的方法，适应不同的需求和性能要求
质量弹簧系统：使用质点弹簧模型来模拟布料的物理行为，包括结构弹簧、剪切弹簧和弯曲弹簧
数值积分：使用Verlet积分法来提高计算效率和数值稳定性
基于位置的动力学：使用PBD方法来处理复杂的约束和保持稳定性
自碰撞处理：通过各种技巧来处理布料的自相交问题，包括加厚、多子步、速度限制和SDF等方法

布料模拟大大提升了游戏的真实感和代入感，是现代游戏开发中不可或缺的重要技术。虽然自碰撞等问题仍然是一个挑战，但随着技术的发展，布料模拟的质量和效率都在不断提高。

11.4 破坏模拟

破坏系统（Destruction System）是游戏物理仿真中的重要组成部分。玩家对场景的破坏是通过破坏系统来实现的。一个好的破坏系统可以极大地提升玩家的游戏体验，有些游戏甚至是以破坏系统为核心玩法进行设计的。

破坏效果至关重要（Destruction effects are crucial）：

不仅是视觉特效（Not just visual effects）：破坏效果不仅仅是视觉上的表现，它能让游戏世界更加生动且富有沉浸感
许多游戏中的核心机制（Core mechanism in many games）：在现代游戏中，破坏系统已经越来越成为一种可以与玩家互动的核心机制

例如，在《彩虹六号：围攻》中，玩家可以在墙上打洞，在什么地方打洞、用什么枪打洞，这已经成为最核心的战术要素。破坏系统给了玩家一种自由，让他们能够创造性地改变游戏世界。

区块层级

我们可以使用一棵树来描述同一物体不同碎片之间的层次关系：树的根节点表示完整的物体，而它下面的每一层表示物体经受一定程度的冲击后所产生的碎片。

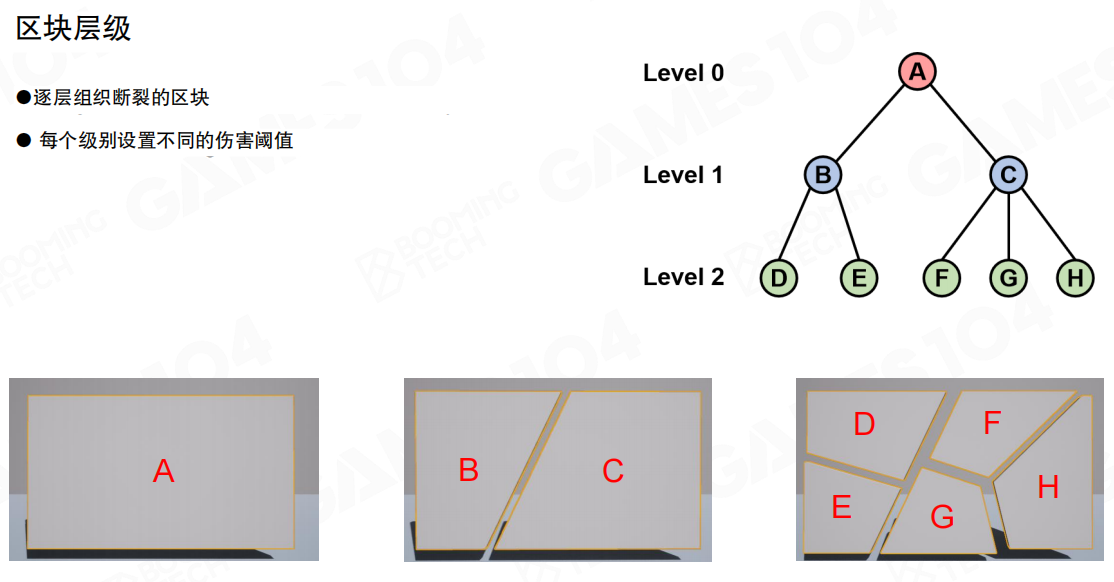
区块层级（Chunk Hierarchy）的组织方式：

逐层组织断裂的区块（Blocks organized to break layer by layer）：将物体按照层级组织成不同的碎片，每一层代表不同级别的破碎
每个级别设置不同的伤害阈值（Each level sets a different damage threshold）：每个层级可以设置不同的伤害阈值，当受到的伤害超过阈值时，该层级的碎片就会断裂

例如，一个完整的物体（A）可以首先断裂成两个较大的碎片（B和C），然后这些碎片可以进一步断裂成更小的碎片（D、E、F、G、H）。这种层级结构让破坏效果看起来更有结构感，而不是一下子全部碎掉。

连通性图

当确定了物体承受的冲击后，就可以使用一张图来表示不同碎片之间的连接关系：图的节点表示碎片，而图的边则表示相互连接的碎片能够承受的荷载。

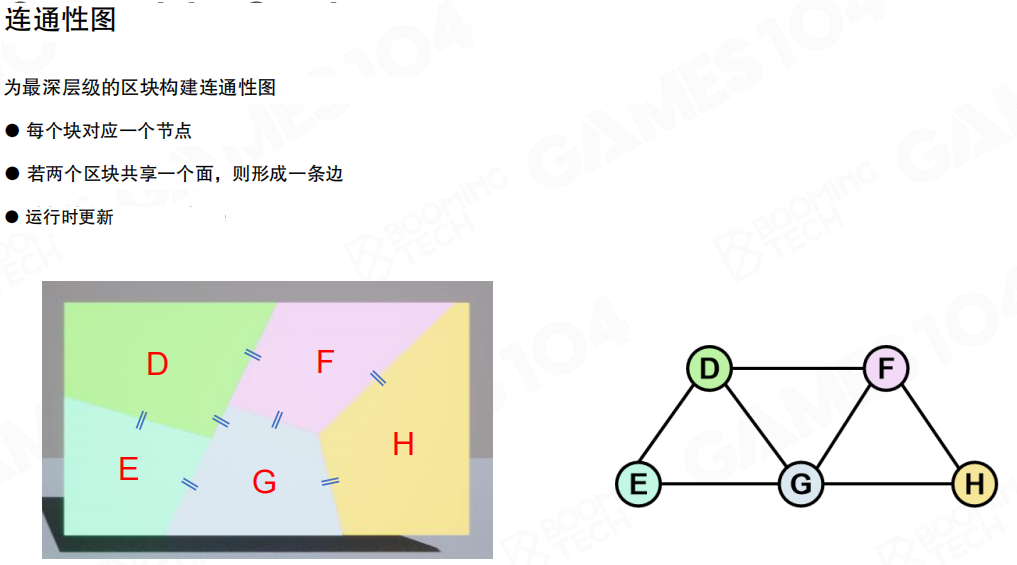
连通性图（Connectivity Graph）的构建：

为最深层级的区块构建连通性图（Constructing a connectivity graph for the deepest level blocks）：为最深层级的碎片构建连通性图
每个块对应一个节点（Each block corresponds to a node）：每个碎片对应图中的一个节点
若两个区块共享一个面，则形成一条边（If two blocks share a face, then an edge is formed）：如果两个碎片共享一个面，则在它们之间形成一条边
运行时更新（Updated at runtime）：连通性图在运行时动态更新，反映碎片之间的连接关系

通过连通性图，我们可以清楚地表示碎片之间的连接关系，当某个连接被破坏时，相应的碎片就会分离。

连接性价值

连通图中每条边上的值表示需要造成多少伤害才能破坏这条边。当冲击大于边上的值时，就会发生物体的破碎。

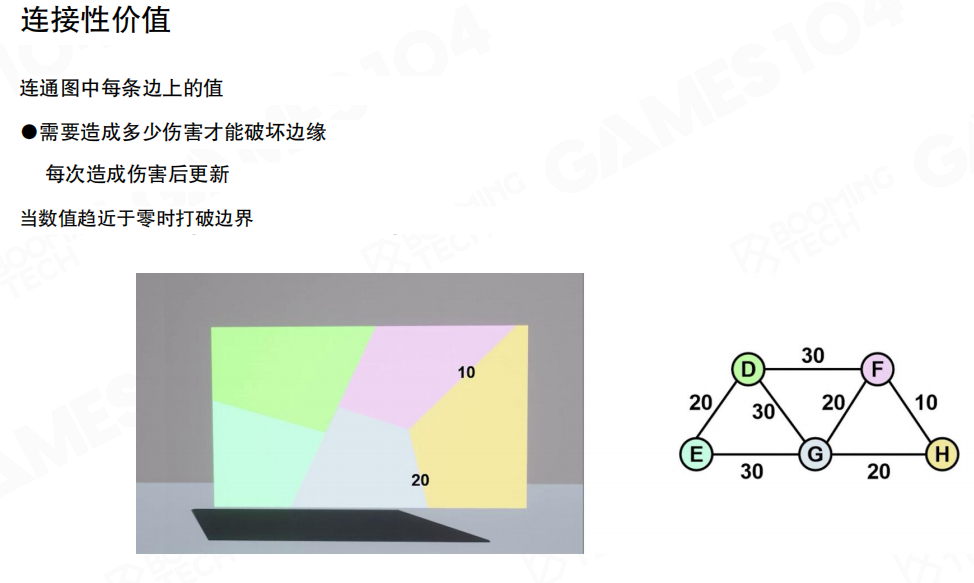
连接性价值（Connectivity Value）的定义：

连通图中每条边上的值（Value on each edge in the connected graph）：每条边都有一个数值，表示该连接能够承受的最大伤害
需要造成多少伤害才能破坏边缘（How much damage is needed to destroy the edge）：当受到的伤害超过这个值时，该连接就会被破坏
每次造成伤害后更新（Update after each damage dealt）：每次受到伤害后，需要更新边的值
当数值趋近于零时打破边界（Break the boundary when the value approaches zero）：当边的值接近零时，该连接就会被破坏，碎片会分离

这个值实际上表示的是连接的”硬度”或”强度”，它决定了碎片之间的连接有多牢固。

伤害计算

需要说明的是，虽然我们使用了冲击和荷载这样的字眼，实际上在游戏引擎中却不会去计算这些物理量。它们只是一些人工设置的数值，并不具备真实的物理意义。在游戏开发中一般会使用一些经验公式来对冲击以及物体的承载力进行计算。

根据冲击点的冲量计算伤害值（Calculate damage value based on the impulse at the impact point）：

I：施加的冲量（例如通过碰撞产生）（Applied impulse (e.g., generated by collision)）
H：刚体的材质硬度（Material hardness of the rigid body）

冲击点处的损伤为（Damage at the impact point is）：
[
D = \frac{I}{H}
]

这个公式非常简单，但实际上存在一些问题。首先，冲量是有量纲的，但”硬度”这个量纲和真实物理学上的量纲不太一致。在真实物理学中，硬度指的是两个东西按在一起，多大的力压下去之后它不会炸掉，而这里指的是在冲击力之下不会炸掉的”硬度”，两者在物理学上的表达是不一样的。

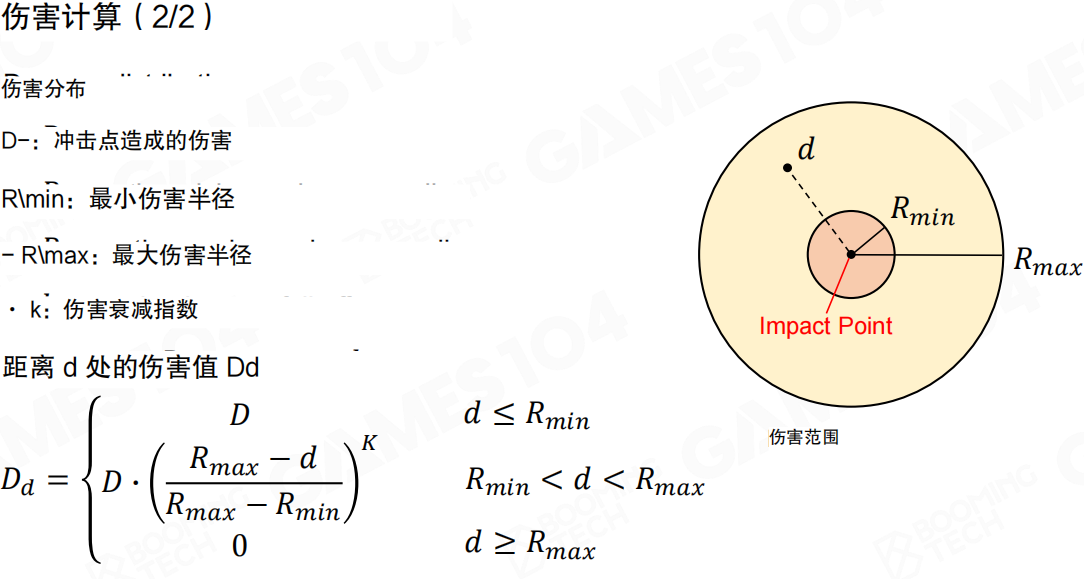
伤害分布（Damage Distribution）：

当有一个球打中一个点的时候，我们会把所有的伤害以一个同心圆的方法分散出去。这个公式看上去特别高大上，实际上非常简单：

D：冲击点造成的伤害（Damage caused at the impact point）
Rmin：最小伤害半径（Minimum damage radius）
Rmax：最大伤害半径（Maximum damage radius）
k：伤害衰减指数（Damage attenuation index）

距离 d 处的伤害值 Dd（Damage value Dd at distance d）：

[
D_d = \begin{cases}
D & \text{如果 } d \leq R_{min} \
D \cdot \left(\frac{R_{max} - d}{R_{max} - R_{min}}\right)^k & \text{如果 } R_{min} < d < R_{max} \
0 & \text{如果 } d \geq R_{max}
\end{cases}
]

在相对小的范围（Rmin）里面，所有人受到的伤害都是一样的。当距离足够远时，伤害逐渐从100%的冲击衰减到0%的冲击，通过插值计算中间的值。

支撑结构

一般我们会做支撑图（Support Graph），就是说物体会挂在某个地方，比如一个窗子就挂在窗框里，如果是在墙上的一个突出部，那就挂在墙上。

有/无支撑结构的破坏效果（Effect of destruction with/without support structure）：

不与世界连接（Not connected to the world）：如果物体不与世界连接，当它受到破坏时，整个物体会完全破碎
连接世界（Connected to the world）：如果物体与世界连接，当它产生破坏时，实际上只会对那个区域产生破坏效果，而不会把整个东西给破坏掉

支撑图的好处是，当物体产生破坏时，它实际上只会对那个区域产生破坏效果，而不会把整个物体给破坏掉。这样可以实现更真实、更可控的破坏效果。

通过沃罗诺伊图构建区块

那么如何去生成这样的碎片呢？在物理引擎中一般会使用Voronoi图（Voronoi Diagram）这样的技术来对原始的物体区域进行划分，划分后的每一个区域即为所需的碎片。

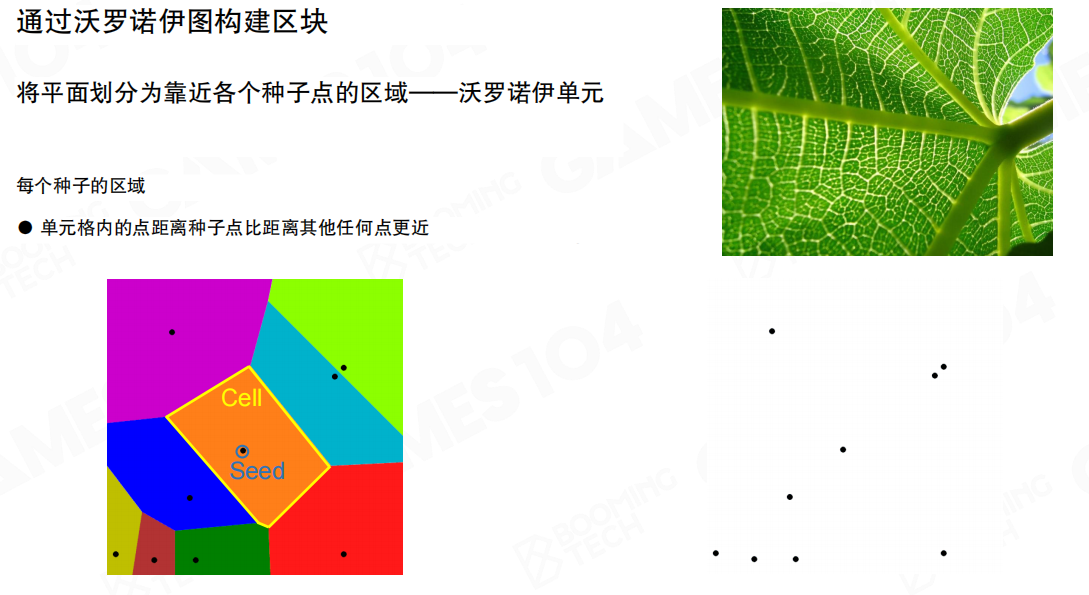
通过沃罗诺伊图构建区块（Constructing blocks using Voronoi diagrams）：

将平面划分为靠近各个种子点的区域——沃罗诺伊单元（Dividing the plane into regions closest to each seed point — Voronoi cells）：将平面或空间划分成多个区域，每个区域内的点距离该区域的种子点比距离其他任何点更近
每个种子的区域（Region for each seed）：每个种子点对应一个区域
单元格内的点距离种子点比距离其他任何点更近（Points within a cell are closer to their seed point than to any other seed point）：这是Voronoi图的基本定义

Voronoi图在生物学上很有用。如果你看过生物课，植物细胞的细胞和细胞壁形成的划分，就是一个标准的Voronoi划分。整个细胞的生长，它非常符合这个数学规律。

基于沃罗诺伊图（Voronoi Diagram）的破碎算法 - 二维网格（Voronoi Diagram-based Fragmentation Algorithm - 2D Grid）：

算法步骤：

在网格的边界矩形内随机选取N个点（Randomly select N points within the bounding rectangle of the grid）：在物体的边界矩形内随机选择N个种子点
构建沃罗诺伊图（Construct a Voronoi Diagram）：根据这些种子点构建Voronoi图
将每个沃罗诺伊单元与网格相交，以获取所有断裂碎片（Intersect each Voronoi cell with the grid to obtain all broken fragments）：将每个Voronoi单元与原始网格相交，得到所有的断裂碎片

通过这种方法，我们可以自动生成看起来很自然、很真实的碎片。数学方法非常简单，但效果却非常好。

三维网格破碎

对于三维的情况则要更加复杂一些，除了需要使用Voronoi图对空间进行划分，还需要使用Delaunay三角化（Delaunay Triangulation）来重新生成碎片的三维网格。

与2D情况类似，但并非微不足道（Similar to 2D cases, but not insignificant）：3D情况与2D类似，但更加复杂
需要为所有断裂表面生成三角形（New triangles need to be generated for all fracture surfaces）：需要为所有断裂表面生成新的三角形网格

在3D情况下，我们使用Voronoi图对空间进行划分后，还需要使用Delaunay三角化算法来重新生成碎片的三维网格。Delaunay三角化是Voronoi图的对偶图，它可以将空间划分成无数个四面体，完成对空间的划分。

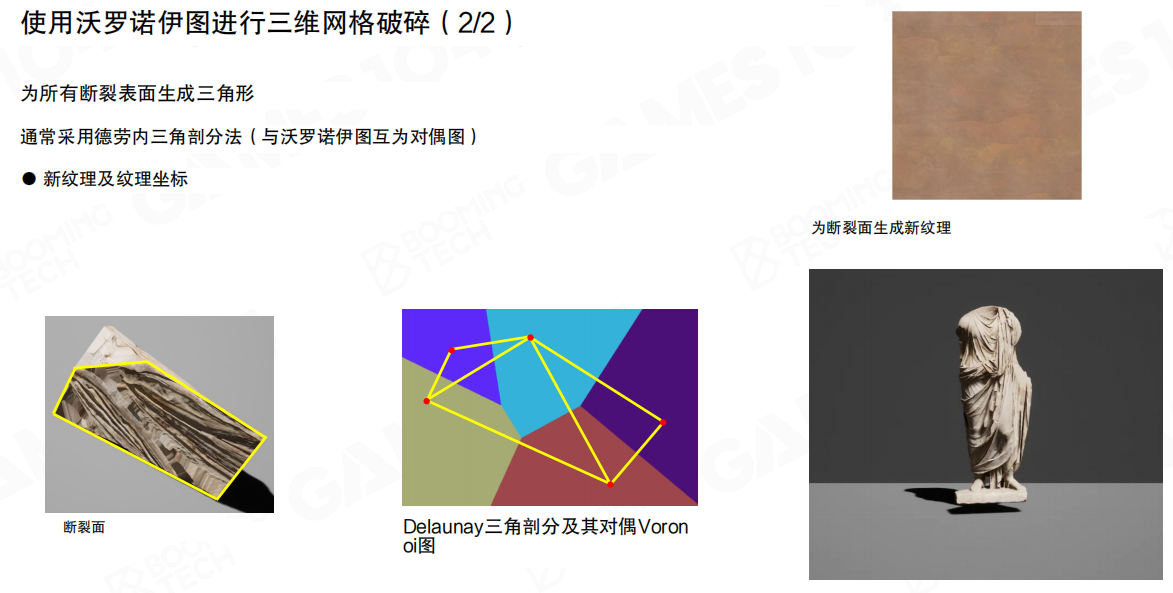
为所有断裂表面生成三角形（Generate triangles for all fractured surfaces）：为所有断裂表面生成新的三角形网格
通常采用德劳内三角剖分法（与沃罗诺伊图互为对偶图）（Delaunay triangulation is usually adopted (which is dual to Voronoi diagrams)）：使用Delaunay三角剖分来生成断裂表面的三角形
新纹理及纹理坐标（New textures and texture coordinates）：当物体破碎后，还需要为碎片的网格赋予内部材质的纹理

断裂面纹理生成（Fractured Surface Texture Generation）：

当一个形体被打碎的时候，最难的一件事情实际上是要生成一个体积纹理（Volume Texture）。比如一个大理石，你把它打碎的时候，在断痕处看到的是很多大理石的花纹。那个花纹实际上是有一个分布的，切口处的纹理生成是比较复杂的。

一般有两种流派：

程序化生成3D纹理：使用程序化方法生成3D的体积纹理，但3D纹理无论从生成到采样都很复杂
离线预计算纹理：离线把这些纹理UV都算好，一旦碎了之后，就把渲染切过去

基于Voronoi图的不同破碎模式（Different Fragmentation Modes Based on Voronoi Diagrams）：

在设置Voronoi图的种子时，还可以根据需要设置不同模式的种子，这样可以实现相应的破碎效果：

均匀随机模式（Uniform Random Mode）：种子点均匀随机分布，产生均匀的破碎效果
聚集模式（Clustering Mode）：种子点聚集在某些区域，产生有大有小的破碎效果
放射状模式（Radial Mode）：种子点呈放射状分布，产生沿着某个方向快速极化的破碎效果，比如玻璃的破碎

这些不同的模式给了美术师更大的空间去表达他们想要表达的世界。

物理系统中的破坏效果

从物理系统的计算流程上来看，破碎系统一般是在碰撞检测之后、实际解算之前。这主要是因为很多破碎的事件是由碰撞所导致的，同时在物体破碎后往往还会产生新的物体（碎片）需要计算相应的运动。

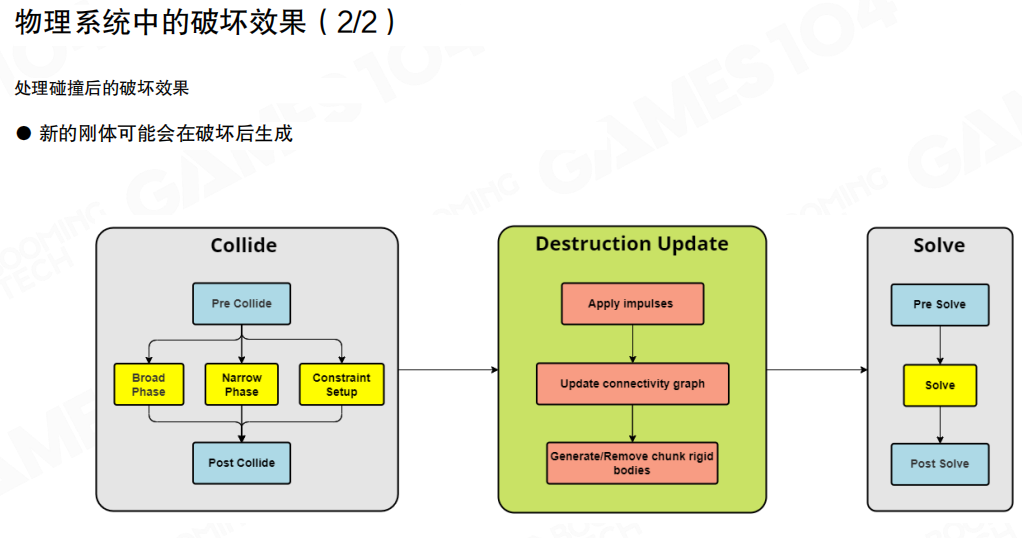
碰撞处理后的破坏效果（Destruction effects after collision processing）：

破坏后可能生成新的刚体（New rigid bodies may be generated after destruction）：当物体破碎后，每个碎片都会变成一个刚体，需要参与物理模拟

破坏更新流程（Destruction Update Pipeline）：

碰撞阶段（Collide）：
- 预碰撞（Pre Collide）
- 宽相位（Broad Phase）和窄相位（Narrow Phase）
- 约束设置（Constraint Setup）
- 后碰撞（Post Collide）
破坏更新阶段（Destruction Update）：
- 施加冲量（Apply impulses）：根据碰撞计算冲量
- 更新连通性图（Update connectivity graph）：更新碎片之间的连接关系
- 生成/移除碎片刚体（Generate/Remove chunk rigid bodies）：根据破坏情况生成或移除碎片的刚体
求解阶段（Solve）：
- 预求解（Pre Solve）
- 求解（Solve）
- 后求解（Post Solve）

更复杂的情况是，一个东西已经碎了，碎片之间还要进行一些互动。这在物理引擎写下来就很麻烦，但确实要写。

使其更加逼真

除了物理系统的计算外，在处理场景破坏时还需要添加相应的声音和粒子效果，这样可以得到更加真实的游戏体验。

使其更加逼真（Make it more realistic）：

仅靠碎裂效果还远远不够（Cracking effects alone are far from enough）：

音效（Sound effects）：当碎片落到地上时，应该听到一些声音
粒子特效（Particle effects）：当破坏生成了一些比较大的碎片，这些碎片落到地上的时候，应该看到一些小小的烟尘
导航更新（Navigation update）：破坏后需要更新导航网格，让AI能够识别新的路径

通过破坏开辟路径（Open a path through destruction）：

在游戏中，破坏不仅可以作为视觉效果，还可以作为游戏机制。例如，玩家可以通过破坏墙壁来开辟新的路径，这需要更新导航系统。

粒子破碎效果（Particle shattering effect）：

对比仅刚体动力学（RBD only）和刚体动力学与粒子（RBD & Particles）的效果，可以看出，添加粒子效果后，破碎效果会显得更加动态、混乱和真实。粒子效果可以模拟细小的碎片、灰尘和烟雾，大大增强了破坏效果的真实感。

破坏效果相关问题

破坏系统的计算是相当昂贵的：当一个物体出现破碎后，往往会带来成百上千个碎片需要进行物理仿真，这会极大地增加物理系统的计算负载。

破坏效果相关问题（Destruction Effect Related Issues）：

谨慎添加破坏效果（Add destruction effects cautiously）：在使用破坏系统时需要慎重考虑
大量碎片可能导致较大的性能开销（A large number of fragments can lead to significant performance overhead）：当物体破碎成成百上千个碎片时，每个碎片都需要参与物理模拟，这会极大地增加计算负载
艺术家在设计破坏效果时通常依赖经验（Artists usually rely on experience when designing destruction effects）：美术师在设计破坏效果时，通常需要依赖经验来设置参数
许多参数需要调整，例如破碎参数（Many parameters need to be adjusted, such as fracturing parameters）：破坏系统有很多参数需要调整，比如破碎参数、伤害阈值等

一些网格断裂参数（Some mesh fracturing parameters）：

点分布类型：Box Distribution（盒子分布）、Cylindrical Distribution（圆柱分布）、Spherical Distribution（球形分布）
参数设置：Num Points（点的数量）、尺寸参数（Width、Length、Height、Radius）、Center Bias（中心偏移）

这些参数需要美术师根据经验进行调整，以达到理想的破碎效果。

主流破坏效果实现方案

目前很多商业引擎都有现成的破坏系统。这些系统提供了完整的工具链和API，让开发者可以更容易地实现破坏效果。

主流破坏效果实现方案（Mainstream Destruction Effect Implementation Solutions）：

目前很多商业引擎都有现成的破坏系统。这些系统提供了完整的工具链和API，让开发者可以更容易地实现破坏效果。

NVIDIA APEX Destruction：

广泛应用于游戏领域（UE4引擎已支持）（Widely applied in game development (UE4 engine already supported)）：APEX Destruction在游戏领域应用广泛，UE4引擎已经支持
官方破坏效果制作工具（PhysX Lab）（Official destruction effect creation tool (PhysX Lab)）：提供了官方的破坏效果制作工具
已于2017年弃用（Deprecated in 2017）：APEX Destruction已经在2017年被弃用

NVIDIA Blast：

APEX的继任者（Successor to APEX）：Blast是APEX的继任者
更优的性能、可扩展性与灵活性（Better performance, scalability, and flexibility）：Blast具有更好的性能、可扩展性和灵活性

NVIDIA Blast在NVIDIA Omniverse中提供了强大的破坏效果支持，可以用于创建逼真的爆炸和破坏效果。

Havok Destruction：

广泛应用于游戏领域（Unity引擎已支持）（Widely applied in the gaming field (Unity engine already supported)）：Havok Destruction在游戏领域应用广泛，Unity引擎已经支持
性能优异且功能多样（Excellent performance and diverse functions）：Havok Destruction性能优异，功能多样
高额授权费用（High licensing fees）：Havok Destruction需要高额的授权费用

Havok Destruction在《战地：硬仗》等游戏中得到了广泛应用，提供了高质量的破坏效果。

Chaos Destruction（Epic Games出品）（Chaos Destruction (Produced by Epic Games)）：

支持完整的工具链（Supports a complete toolchain）：Chaos Destruction提供了完整的工具链
UE5中仍为测试版本（Still a test version in UE5）：在UE5中，Chaos Destruction仍然是测试版本

Chaos Destruction号称是完全用XPBD算法实现的，号称是性能最强的物理引擎，但在目前的游戏行业中，实战中用的还不多，所以这个东西还有待观察。

总结

破坏模拟是游戏引擎中一个非常重要且复杂的系统。它通过以下方式实现了真实的场景破坏效果：

层级结构：使用树状结构组织碎片，实现逐层破坏
连通性图：使用图结构表示碎片之间的连接关系
伤害计算：根据冲量和材质硬度计算伤害，并通过距离衰减分布伤害
支撑结构：通过支撑图实现局部破坏，而不是整体破坏
Voronoi图：使用Voronoi图自动生成自然的碎片形状
3D网格处理：使用Delaunay三角化生成断裂表面的网格
纹理生成：为断裂表面生成合适的纹理，增强真实感
物理集成：将破坏系统集成到物理引擎的计算流程中
效果增强：通过音效、粒子特效等增强破坏效果的真实感

破坏系统大大提升了游戏的真实感和沉浸感，是现代游戏开发中不可或缺的重要技术。虽然破坏系统的计算成本很高，但随着硬件性能的提升和算法的优化，破坏效果的质量和效率都在不断提高。

11.5 载具模拟

载具系统（Vehicle System）是现代游戏中重要的组成部分。要对载具进行模拟需要推导相应的动力学模型，以汽车为例，整个汽车可以看做通过悬挂系统与地面接触的刚体。

车辆实现谱系（Vehicle Implementation Lineage）：

从风格化（Stylized）到逼真（Realistic），游戏中的车辆模拟有不同的实现方式：

风格化：如《马里奥赛车8豪华版》，使用卡通风格，注重趣味性而非真实性
半真实：如《侠盗猎车手V》，在真实感和游戏性之间取得平衡
高度真实：如《极限竞速：地平线4》，追求接近真实的物理表现
完全真实：如《GT赛车7》，完全模拟真实驾驶体验

不同的游戏类型需要不同层次的物理模拟精度。对于赛车游戏来说，真实的物理模拟是核心玩法的重要组成部分。

车辆机构建模

要对载具进行模拟，首先需要建立车辆的机构模型。整个汽车可以看做通过悬挂系统与地面接触的刚体。

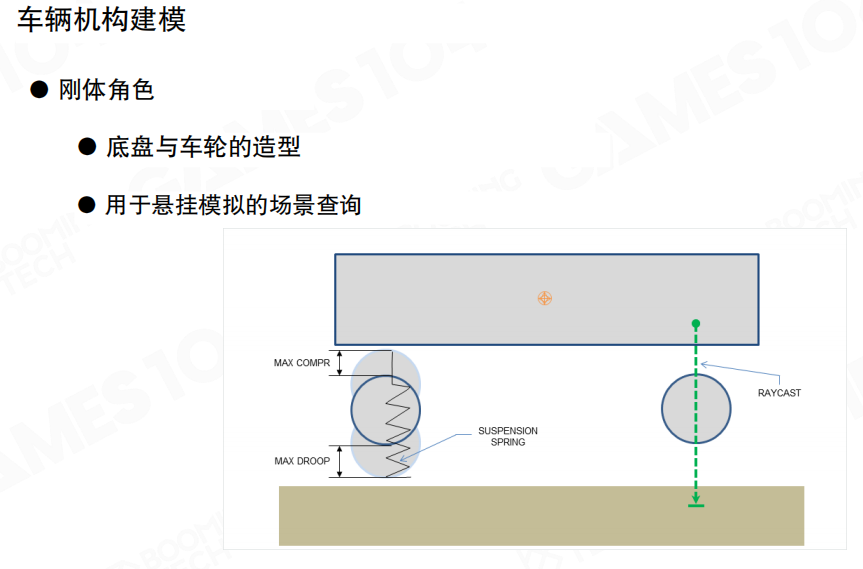
关键要素：

刚体角色（Rigid Body Role）：整个车身作为一个刚体，通过悬挂系统与地面接触
底盘与车轮的造型（Chassis and Wheel Modeling）：底盘和车轮的几何形状和物理属性
用于悬挂模拟的场景查询（Scene Query for Suspension Simulation）：使用射线检测（Raycast）来检测地面，计算悬挂系统的压缩和拉伸

悬挂系统（Suspension System）：

悬挂系统是连接车身和车轮的关键部件。在模拟中，悬挂系统可以简化为弹簧：

最大压缩（MAX COMPR）：悬挂系统允许的最大压缩距离
最大下垂（MAX DROOP）：悬挂系统允许的最大拉伸距离
射线检测（RAYCAST）：从底盘向下发射射线，检测地面距离，用于计算悬挂的压缩量

悬挂系统让车辆能够适应地面的起伏，产生上下振动，这是车辆模拟的基础。

牵引力

整个汽车的驱动力来自于引擎产生的扭矩。引擎会输出一个扭矩，这个扭矩需要经过变速箱和差速器传递到车轮，最终转化为推动车辆前进的牵引力。

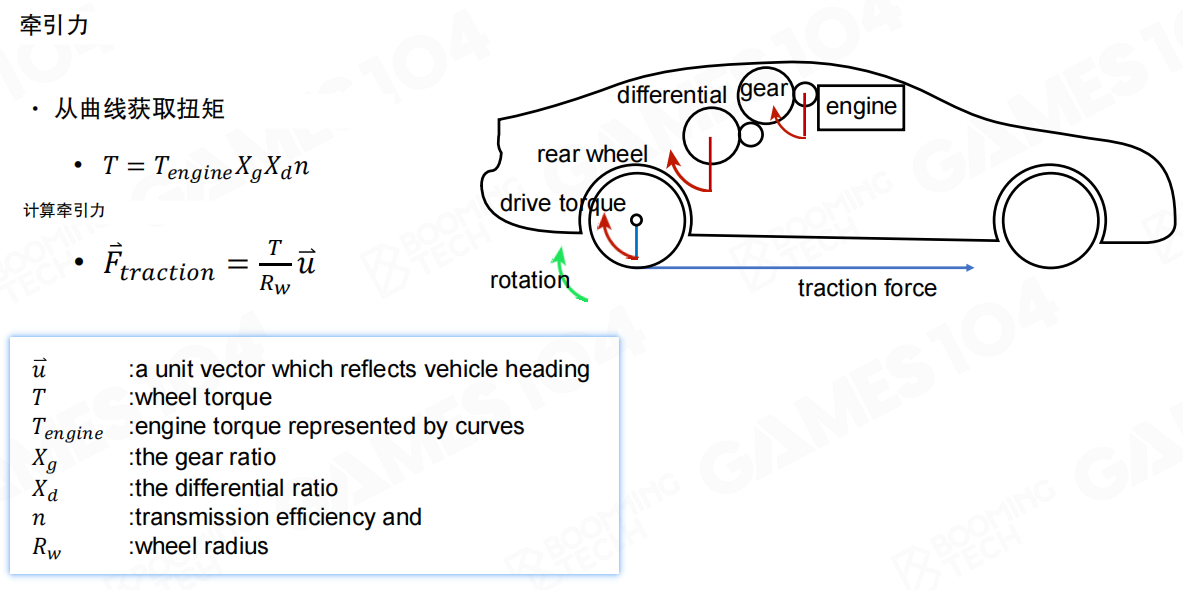
从曲线获取扭矩（Obtaining Torque from Curves）：

引擎的扭矩与转速和油门有关，通常通过查表或曲线来获取：

[
T = T_{engine} \cdot X_g \cdot X_d \cdot n
]

其中：

T：车轮扭矩（Wheel torque）
T_engine：引擎扭矩（Engine torque），由曲线表示
X_g：齿轮比（Gear ratio）
X_d：差速器比（Differential ratio）
n：传动效率（Transmission efficiency）

计算牵引力（Calculating Traction Force）：

[
\vec{F}_{traction} = \frac{T}{R_w} \cdot \vec{u}
]

其中：

F_traction：牵引力（Traction force）
R_w：车轮半径（Wheel radius）
u_vector：反映车辆朝向的单位向量（Unit vector which reflects vehicle heading）

动力传递流程：

引擎 → 变速箱（齿轮） → 差速器 → 驱动轮 → 牵引力

牵引力实际上是轮胎与地面之间的静摩擦力。只要轮胎不打滑（不漂移），它和地面的摩擦关系就是静摩擦关系，始终在接触点上形成一个连接。

悬挂力

在竖直方向上，由于地面的起伏，车身会产生悬挂系统所导致的振动。悬挂力是连接底盘和悬挂系统的力，每个车轮独立计算。

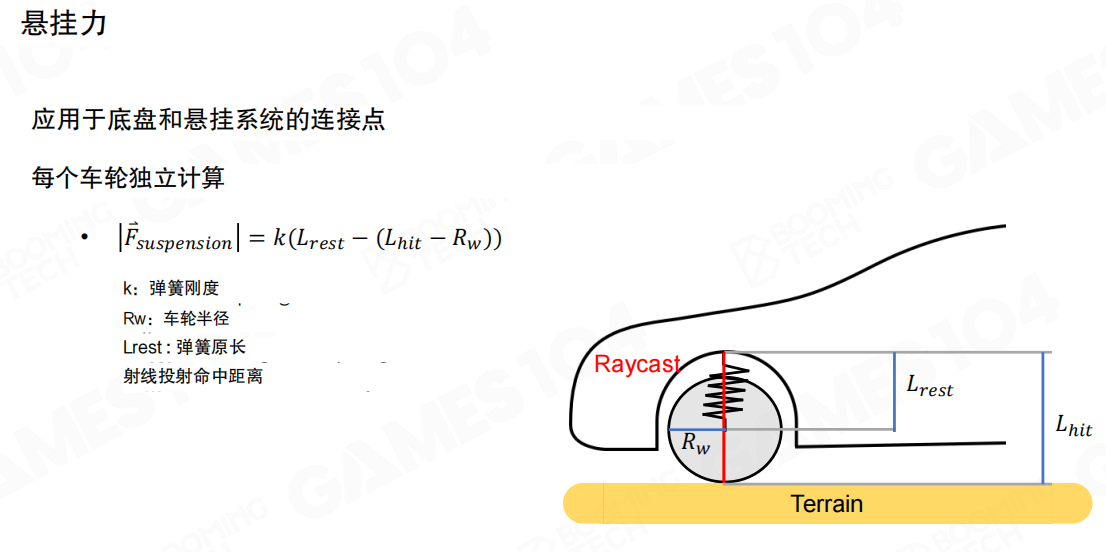
应用于底盘和悬挂系统的连接点（Applied to connection points of chassis and suspension system）

每个车轮独立计算（Calculated independently for each wheel）

悬挂力公式：

[
|F_{suspension}| = k(L_{rest} - (L_{hit} - R_w))
]

其中：

k：弹簧刚度（Spring stiffness）
R_w：车轮半径（Wheel radius）
L_rest：弹簧原长（Spring original length / resting length）
L_hit：射线投射命中距离（Raycast hit distance）

悬挂力计算原理：

使用射线检测（Raycast）从悬挂连接点向下检测地面距离（L_hit）
减去车轮半径（R_w），得到从悬挂连接点到车轮底部的距离
与弹簧原长（L_rest）比较，计算弹簧的压缩量
根据胡克定律，压缩量乘以弹簧刚度（k）得到悬挂力

悬挂力让车辆能够适应地面的起伏，产生上下振动。如果轮胎放长了，车就会往下压；如果从一个坡下来之后，车身往下惯性，悬挂就会试图把车往上顶。因为有四个轮子、四个悬挂，所以车会出现左摇右晃的现象。

轮胎力

在平面上，汽车的轮胎会产生平行于前进方向的径向力，同时还会产生切向力控制车辆的转动。

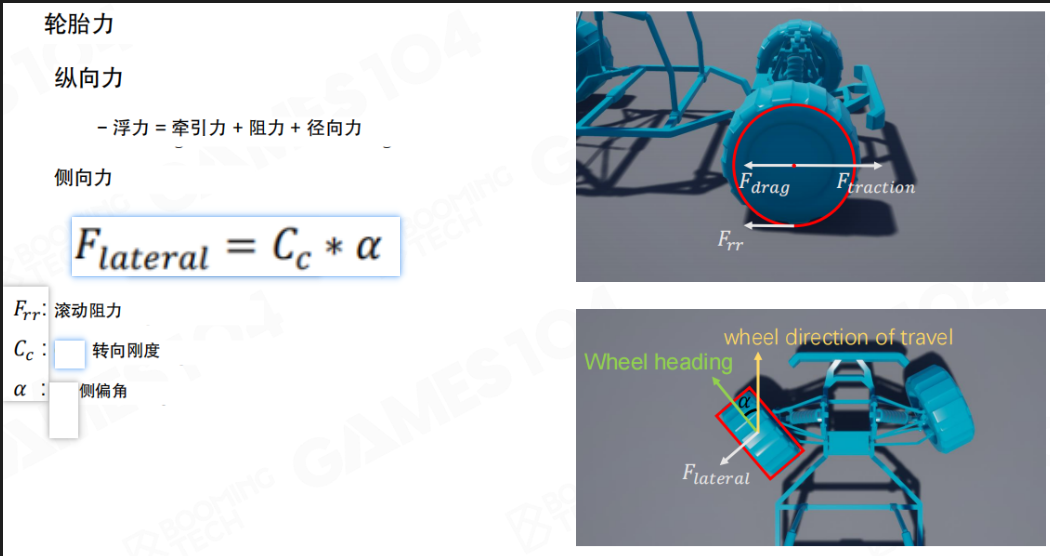
轮胎力比大家想象的比较复杂，主要包括两种：

纵向力（Longitudinal Force）：

浮力 = 牵引力 + 阻力 + 径向力（Buoyancy = Traction + Resistance + Radial Force）
Frr：滚动阻力（Rolling Resistance）

纵向力包括：

牵引力（Traction）：如果是驱动轮，包括引擎产生的驱动力
阻力（Resistance）：如果是前轮的导向轮，主要是阻力
滚动阻力（Frr）：轮胎与地面接触产生的滚动摩擦

侧向力（Lateral Force）：

[
F_{lateral} = C_c \cdot \alpha
]

其中：

Cc：转向刚度（Cornering Stiffness）
α：侧偏角（Slip Angle）

侧向力原理：

当轮胎打了一个方向之后，移动方向是A，但轮胎往另一个方向走，会产生一个切向力。这个切向力实际上是一个滑动摩擦力，是汽车很重要的导向力。

这个力的大小既受制于摩擦系数，也受制于重心。重心越靠前，前轮的压力越大；重心越后，后轮压力越大。所以重心也会影响到整个力的分布。

如果我们解一个车的导向方程，你会发现要把这两个力分开算，才能算出来车有多大的力气往一边去转。而且你会发现为什么轮胎打了之后，它会有的时候会出现打滑，其实也是这个道理，因为每一个摩擦力都有上限。

质心

根据车身重量的分布，我们还需要计算汽车的重心。实际上重心的位置不仅会控制汽车的振动，还会对汽车的转向性能有重要的影响。

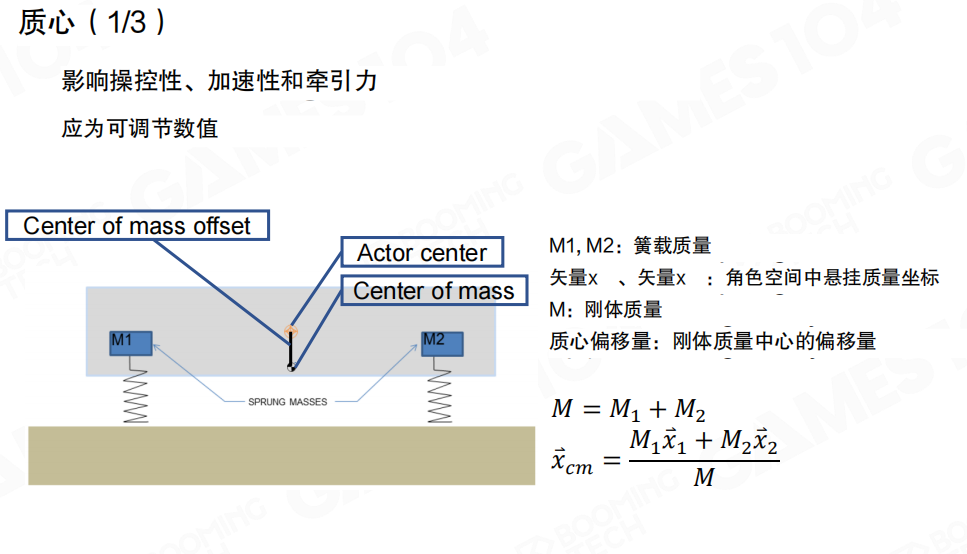
影响操控性、加速性和牵引力（Affects handling, acceleration, and traction）

应为可调节数值（Should be an adjustable value）

质心计算公式：

对于两个簧载质量（M1和M2）的系统：

[
M = M_1 + M_2
]

[
\vec{x}_{cm} = \frac{M_1\vec{x}_1 + M_2\vec{x}_2}{M}
]

其中：

M1, M2：簧载质量（Sprung mass）
矢量x₁, 矢量x₂：角色空间中悬挂质量坐标（Coordinates of suspended mass in character space）
M：刚体质量（Rigid body mass）
质心偏移量：刚体质量中心的偏移量（Center of mass offset: Offset of the rigid body’s center of mass）

质心实际上是前后两个支点（前轮组、后轮组）中间的那个重量的中心点。这个点很多时候也是车最关键的一个属性。对车的重心影响最大的东西，至少在汽油车时代，是那个发动机。因为汽油车有发动机的密度是最大的，一个大铁坨子放到前面重心就靠前了，放到后面重心就靠后了。

影响车辆在空中的稳定性（Factors affecting vehicle stability in the air）：

前重后轻 → 俯冲（Front heavy, rear light → Nose dive）：如果重心太靠前，当车子飞升的时候，它就很容易一头栽下去，车子就不太稳定
后部重量偏大 → 稳定化（Rear weight biased -> Stabilization）：如果重心偏后，这个车在飞跃的时候相对稳定

大家如果玩过拉力赛车，就会知道这个点好像很重要。所以我们经常讲的汽车调校，重心是一个重要的参数。

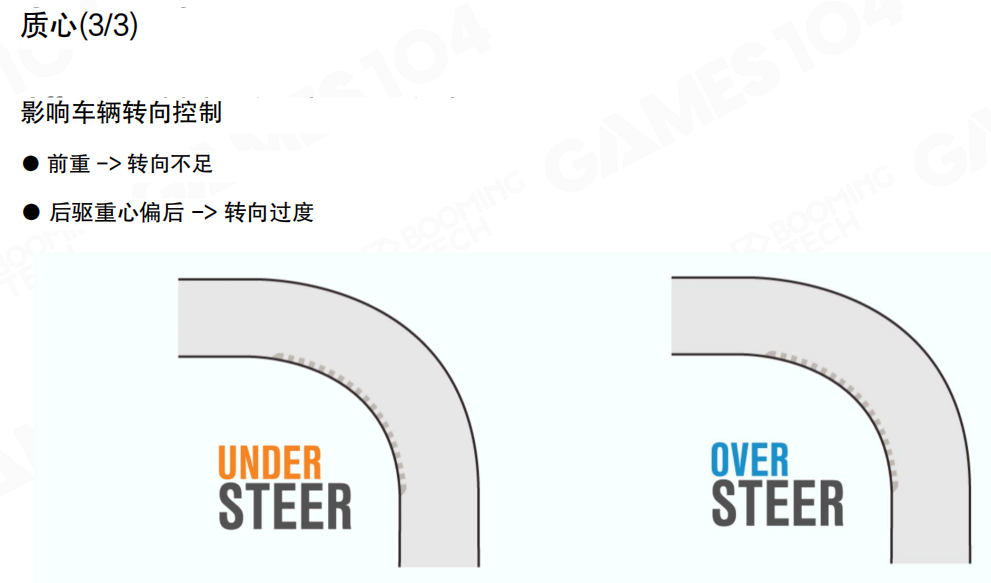
影响车辆转向控制（Affects vehicle steering control）：

前重 → 转向不足（Front-heavy -> Understeer）：一般来讲如果重心比较靠前，那汽车拐弯的时候，它的转向力就不足
后驱重心偏后 → 转向过度（Rear-wheel drive, center of gravity biased to the rear -> Oversteer）：后驱车如果重心偏后，会导致转向过度

转向不足和转向过度（Understeer and Oversteer）：

转向不足（Understeer）：车辆的实际转弯半径大于理想转弯半径，车辆倾向于保持直线行驶
转向过度（Oversteer）：车辆的实际转弯半径小于理想转弯半径，后轮容易打滑

原理分析：

当重心靠前的时候，相对于转动中心，转向的力臂不够长，所以它的扭矩不够大，所以转向是不足的。这就是我们讲的前驱车，因为发动机靠前导致它的转向不足。

但是像一些跑车的时候，它的发动机会逐渐的往后靠，它的重心就往中间往中间一点。但这个时候它的驱动又在后面，它的导向就在前面，这个车的转向性能就会好于那些前驱车。

权重转移

同时需要注意的是，当车辆进行加速或是刹车时，重心的位置也会发生一些变化。这叫做权重转移（Weight Transfer）。

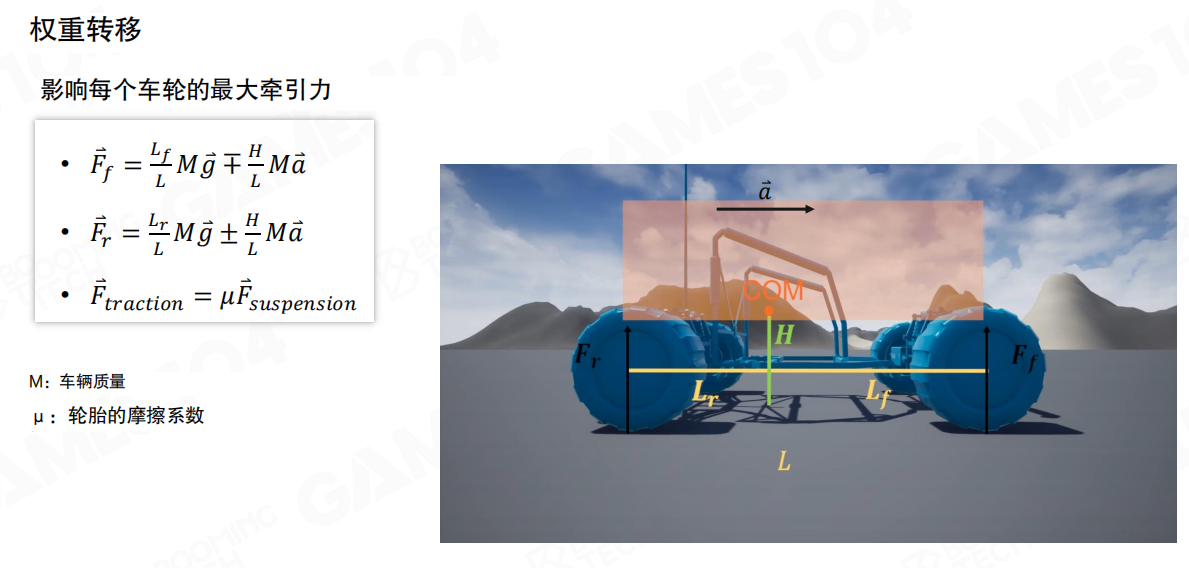
权重转移（Weight Transfer）：

影响每个车轮的最大牵引力（Affects the maximum traction of each wheel）

前后轮法向力计算：

[
F_f = \frac{L_r}{L} \cdot M \cdot g \pm \frac{H}{L} \cdot M \cdot a
]

[
F_r = \frac{L_f}{L} \cdot M \cdot g \mp \frac{H}{L} \cdot M \cdot a
]

其中：

F_f：前轮法向力（Normal force on front wheel）
F_r：后轮法向力（Normal force on rear wheel）
M：车辆质量（Vehicle mass）
g：重力加速度
a：加速度（Acceleration）
H：质心高度（Height of center of mass）
L：轴距（Wheelbase）
L_f：前轴到质心的距离（Distance from front axle to center of mass）
L_r：后轴到质心的距离（Distance from rear axle to center of mass）

最大牵引力：

[
F_{traction} = \mu \cdot F_{suspension}
]

其中：

μ：轮胎的摩擦系数（Tire friction coefficient）

权重转移原理：

当车辆加速时，重心会稍微往后移那么一点点。大家如果自己开过车，就知道会有一种感觉，好像感觉车子一加速，整个车头好像稍微抬那么一点点。减刹车的时候，你会觉得车头稍微按下去一点点，你的重心其实也有一点点的偏差。

这个权重转移实际上在汽车的动力学模拟的时候，也是一个很重要的东西。它会影响每个车轮的最大牵引力，因为牵引力等于摩擦系数乘以法向力。当权重转移到后轮时，后轮的法向力增加，最大牵引力也增加；前轮的法向力减少，最大牵引力也减少。

转向角度

为了更好地实现转向，现代汽车在设计时会让两个转向轮的转动有微小的差异。在进行模拟时也需要考虑这个微小的角度变化。这叫做阿克曼转向（Ackermann Steering）。

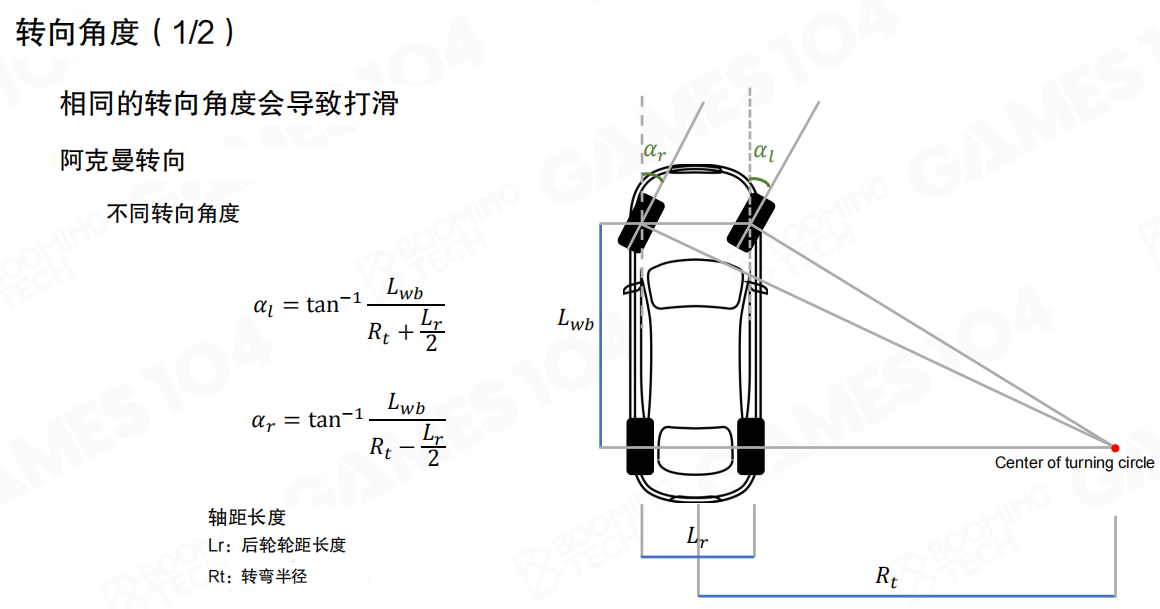
阿克曼转向原理：

如果汽车的两个导向轮假设都打一样的方向角的时候，其实它外侧的轮实际上是空转的，它是在那被拖着走的，它的转向力其实是不足。

所以它有一个数学的方法，就是内侧的轮它实际上转的更多一点，而外侧的轮转的稍微小一点，它指向是一个很远的一个旋转中心，然后以他那个连接线做垂线决定我的角度。

转向角度计算公式：

[
\alpha_l = \tan^{-1}\left(\frac{L_{wb}}{R_t + L_r/2}\right)
]

[
\alpha_r = \tan^{-1}\left(\frac{L_{wb}}{R_t - L_r/2}\right)
]

其中：

αl：左轮（内侧）转向角（Steering angle for left (inner) wheel）
αr：右轮（外侧）转向角（Steering angle for right (outer) wheel）
L_wb：轴距长度（Wheelbase length）
L_r：后轮轮距长度（Rear wheel track length）
R_t：转弯半径（Turning radius）

无阿克曼转向（No Ackermann Steering）vs 采用阿克曼转向原理（Using Ackermann Steering Principle）

对比效果：

无阿克曼转向：两个前轮转向角度相同，外侧轮会被拖着走，导致轮胎打滑，转向不稳定
采用阿克曼转向：内侧轮转向角度更大，外侧轮转向角度较小，所有轮子都围绕一个共同的旋转中心转动，转向更加稳定和流畅

阿克曼转向的重要性：

大家不要觉得这种很高深，如果大家学的是汽车的工程学的话，这就是一个标配，就是现在所有的汽车它里面都有这个系统，所以才使得我们驾驶起来觉得这个车好像很丝滑。

但实际上人家做了一个非常精细的一个数学运算。如果没有这个角度的处理的话，你会发现就是你的这个旋转的话，它会非常的不稳定，它就会变成一个螺旋衰减线。但是如果你有了这个阿克曼角度的处理，你就可以让这个车开出一个完美的弧线。

高级车轮接触

最后需要说明的是，在计算地面和车轮求交时，需要把轮子看做是球，这样才能模拟出车辆在凹凸不平的地面上行驶的效果。

单射线检测（Single Raycast）vs 球体扫描（Spherecast）

对比效果：

单射线检测：使用简单的射线检测，轮胎与地面接触不够精确，轮胎可能”漂浮”在尖锐边缘上方，接触点不准确
球体扫描：使用球体或圆形进行扫描检测，轮胎能够更真实地贴合地面，特别是在凹凸不平的地面上，接触点更加准确

球体扫描的优势：

在真实的赛车游戏里面，我们都会用一个球或者用一个圆去做这个扫描（Sweep），这样就能知道跟这个环境真实的交点在哪里。这样的话你的整个这个运动看上去就更加真实。

球体扫描能够模拟轮胎的圆形形状，让车辆在凹凸不平的地面上行驶时，轮胎能够更准确地贴合地面，产生更真实的悬挂压缩和车辆运动效果。

总结

载具模拟是游戏引擎中一个非常重要且复杂的系统。它通过以下方式实现了真实的车辆物理反应：

车辆机构建模：将车辆简化为刚体、底盘、车轮和悬挂系统的组合
牵引力计算：从引擎扭矩经过变速箱和差速器传递到车轮，转化为牵引力
悬挂力计算：使用射线检测计算悬挂系统的压缩，产生悬挂力
轮胎力：包括纵向力（牵引力、阻力）和侧向力（转向力）
质心计算：质心位置影响操控性、加速性、空中稳定性和转向性能
权重转移：加速和刹车时重心的变化影响各轮的最大牵引力
阿克曼转向：不同转向角度让所有轮子围绕共同旋转中心转动
高级车轮接触：使用球体扫描实现更精确的地面接触检测

有了以上的这些所有的模型之后，就用我们前面讲的那种弹簧质点、速度、惯性这些动力学，其实就可以做一个非常简单的汽车模拟游戏了。

而且这个东西非常的有意思，因为调校它的每一个参数，比如说那个轮胎的摩擦力、发动机的扭矩和他那个发动机的扭矩随着转速的变化曲线、包括重心的位置，可以做出各种各样不同质感的车了。

载具系统的扩展：

虽然我们学会了这些载具系统，但还有很多扩展应用：

坦克：使用履带系统，比轮式车辆更复杂
飞机：飞行模拟系统，涉及空气动力学
船舶：船舶模拟系统，涉及流体动力学

这些都需要更专业的物理模型，但基本原理是相通的。

11.6 高级：PBD与XPBD

PBD（Position-Based Dynamics，基于位置的动力学）和XPBD（Extended Position-Based Dynamics，扩展基于位置的动力学）是两种更高级的物理仿真技术。和前面介绍过的仿真技术相比，PBD和XPBD是建立在拉格朗日力学（Lagrangian mechanics）基础上的仿真方法。

在拉格朗日力学的框架中，不再考虑力等物理概念，而是把物理定律视为系统的某种约束来描述运动。这种思维方式非常巧妙，它把整个力学的规律描述成一系列的约束，然后用约束去反向定义运动。

回顾：约束求解（Review: Constraint Solving）

基于拉格朗日力学的建模约束（Modeling Constraints Based on Lagrangian Mechanics）

在拉格朗日力学中，物理系统被描述为约束：

碰撞约束（Collision Constraints）：
- 无穿透（No Penetration）
- 摩擦力（Friction）
- 恢复系数（Coefficient of Restitution）
布料约束（Cloth Constraints）：
- 拉伸（Stretch）
- 弯曲（Bend）

拉格朗日力学是一个非常了不起的数学框架。它把很多力学的计算变成了一个求解约束的问题。这种方法的优势在于，它不需要直接计算力和加速度，而是通过约束来反向求解运动。

圆周约束

以匀速圆周运动为例，在拉格朗日力学中我们不会去计算各种改变质点运动状态的力，而是考虑质点运动的位置约束以及速度约束。

位置约束（Position constraint）：

[
C(x) = ||x|| - r = 0
]

这个约束表示，质点的位置向量x的模长减去半径r必须等于零，即质点始终保持在距离原点为r的圆周上。

速度约束（Velocity constraint）：

[
\frac{d}{dt} C(x) = \frac{dC}{dx} \cdot \frac{dx}{dt} = 0
]

其中：

(\frac{dC}{dx})：雅可比矩阵（Jacobian），用J表示
(\frac{dx}{dt})：速度向量，用v表示

因此，速度约束可以表示为：(J \cdot v = 0)

雅可比矩阵（Jacobian）：

J：行向量（Row Vector）
Jᵀ垂直于v：(J^T \cdot v = 0)
功能：将速度转换为速度约束（Transforms velocity to velocity constraint）

雅可比矩阵是一个非常了不起的数学观察。它表示当系统发生微小扰动时，约束的变化趋势。在迭代法中，雅可比矩阵告诉我们沿着哪个方向尝试，能以最快的速度收敛到满足约束的点。

字符串约束

类似地，弹簧质点系统也可以表示为由约束定义的系统。

拉伸约束公式：

[
C_{stretch}(x_1, x_2) = ||x_1 - x_2|| - d
]

其中：

x₁, x₂：两个质点的位置
d：弹簧的原始长度（Rest length）

拉伸情况（Stretching Case）：

当两个质点之间的距离大于原始长度d时，约束会推动它们靠近，使距离回到d。

压缩情况（Compression Case）：

当两个质点之间的距离小于原始长度d时，约束会推动它们远离，使距离回到d。

对于弹簧质点模型，你可以用这种约束去表达。当你有两个支点x₁和x₂时，它们可以乱动，但是它们中间应该满足这个约束，就是它要回到它的Rest pose。实际上它的约束就是x₁减x₂，它两个之间的距离（模长）减去Rest pose的距离等于零。这就是对一个弹簧的约束。

PBD约束投影

PBD在求解时，会把整个物理系统描述为关于位置的约束。然后通过不断迭代来计算满足约束的解。

位置向量定义：

[
X^{(k)’} = [x_1^{(k)’}; …; x_n^{(k)’}]
]

其中：

k=0：积分位置（Integrated position）
k>0：根据上一轮迭代修正后的位置（Position corrected based on the previous iteration）

约束满足方程：

使用一阶泰勒展开近似约束函数：

[
C(X^{(k)’} + \Delta X) \approx C(X^{(k)’}) + \nabla_X C(X^{(k)’}) \cdot \Delta X = 0
]

位置修正：

[
\Delta X = \lambda \nabla_X C(X^{(k)’})
]

位置修正ΔX与约束函数的梯度∇_X C成正比，比例系数为λ。

PBD约束投影推导：

通过代入和求解，可以得到：

[
\lambda = -\frac{C(X^{(k)’})}{||\nabla_X C(X^{(k)’})||^2}
]

[
\Delta X = -\frac{C(X^{(k)’})}{||\nabla_X C(X^{(k)’})||^2} \nabla_X C(X^{(k)’})
]

这个公式的核心思想是：假设当前点在约束函数C(X)的外面，我们要求C(X + ΔX) = 0。先用泰勒展开把C(X + ΔX)展开，然后把高阶项全部扔掉（因为ΔX非常小）。接下来假设ΔX的方向一定是沿着雅可比矩阵的切线方向去走，然后反向带回来，就可以算出λ是多少。算出了λ，又知道了要走的方向，把λ乘上雅可比矩阵给定的方向，实际上就是我们要的这个一次迭代的补偿。

PBD工作流程

整个PBD的求解流程如下：

基于位置的动力学——工作流程（Position-Based Dynamics — Workflow）：

(1) forall vertices i
(2) initialize x_i = x_i^0, v_i = v_i^0, w_i = 1/m_i
(3) endfor
(4) loop
(5)     forall vertices i do v_i ← v_i + Δt w_i f_ext(x_i)
(6)     dampVelocities(v_1, ..., v_N)
(7)     forall vertices i do p_i ← x_i + Δt v_i
(8)     forall vertices i do generateCollisionConstraints(x_i → p_i)
(9)     loop solverIterations times
(10)        projectConstraints(C_1, ..., C_M+M_coll, p_1, ..., p_N)
(11)    endloop
(12)    forall vertices i
(13)        v_i ← (p_i - x_i) / Δt
(14)        x_i ← p_i
(15)    endfor
(16)    velocityUpdate(v_1, ..., v_N)
(17) endloop

初始化阶段（步骤1-3）：

为每个顶点初始化位置x_i、速度v_i和逆质量w_i（等于1除以质量m_i）。

半隐式积分（Semi-implicit integration，步骤5-7）：

步骤5：根据外力更新速度
步骤6：应用速度阻尼
步骤7：根据速度预测新位置

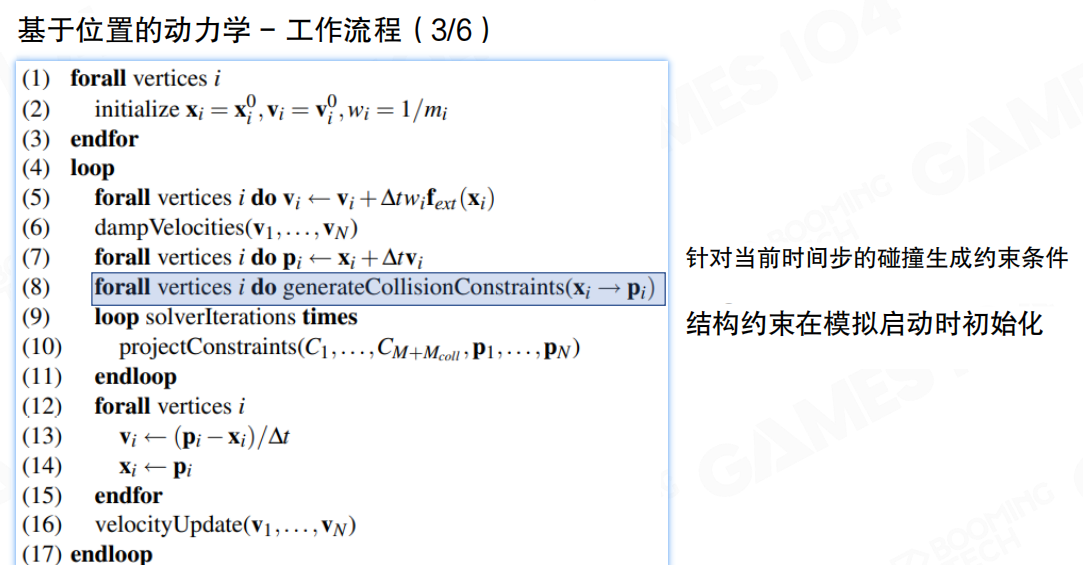
碰撞约束生成（步骤8）：

针对当前时间步的碰撞生成约束条件（Generate collision constraints for the current time step）

在每一帧里面，先根据速度预测位置。但是当前这个位置算出来的时候，实际上很多时候可能是有问题的，它可能有穿插，它可能钻到地下去了。用generateCollisionConstraints把这些碰撞的约束也算出来了。

结构约束在模拟启动时初始化（Structural constraints are initialized at the start of the simulation）

求解器迭代（Solver Iterations，步骤9-11）：

通过迭代调用projectConstraints来投影所有约束，包括：

结构约束（C₁到C_M）：布料本身的不能被拉伸的约束
碰撞约束（M_coll）：不能穿模、不能自我碰撞的约束

迭代会一直进行，直到：

所有约束的误差小于某个给定的epsilon（小的值）
或者已经迭代了足够多的次数

求解器迭代后更新状态（Update state after solver iteration，步骤12-15）：

步骤13：根据修正后的位置更新速度
步骤14：更新位置到修正后的位置

速度更新（步骤16）：

根据摩擦系数和恢复系数修改碰撞顶点的速度（Modify the velocity of collision vertices according to friction coefficient and restitution coefficient）

这一步很重要，因为如果不加上一个速度的阻尼的话，PBD的求解器很可能会不稳定，会炸掉。这个阻尼是一定要加的。

PBD的优势

PBD是目前游戏行业非常热门的物理仿真技术，和传统仿真技术相比，PBD往往会得到更稳定的解。

将约束条件投影为位置修正（Projects constraints as position corrections）：PBD把所有的物理规律都抽象成约束，包括碰撞也变成约束，避免了传统牛顿力学中可能导致不稳定的速度、加速度计算
快速稳定，适用于大多数情况（Fast and stable, suitable for most situations）：PBD的收敛会很快，比较稳定，不太容易出现异常的情况

难以控制约束满足（Difficult to control constraint satisfaction）：

不能将碰撞约束的优先级置于其他约束之上（Cannot prioritize collision constraints over other constraints）

常用于游戏中的布料模拟（Commonly used in cloth simulation in games）：

在布料系统里面，PBD是一个非常重要的方法，基本上大家现在都在用PBD了。比如NVIDIA FleX就是基于PBD的物理引擎。

PBD最核心的一个点就在于，它因为把所有的物理学的规律都抽象成约束了，包括比如像碰撞，它也是把它变成一个约束了。那你以前在解这种牛顿力学的这种速度、加速度这些，可能会导致你的这个iteration或者simulation不稳定的东西的话，把它给优化掉了。

XPBD：扩展位置动力学

XPBD可以看做是对PBD的一种推广，它在PBD的基础上引入了刚度（stiffness）的概念来描述不同约束的强弱。

核心概念：

使用柔度作为约束刚度的倒数来处理（Treating compliance as the reciprocal of constraint stiffness）
无限刚度约束（刚体）（Infinite stiffness constraint (rigid body)）
将刚体方向重新引入XPBD以应用于刚体仿真（Reintroducing rigid body orientation into XPBD for rigid body simulation）

虚幻引擎Chaos物理系统（Unreal Engine Chaos Physics System）：

虚幻引擎5自己猛推的属于自己的那个Chaos物理引擎，它自称就是用的XPBD。

能量函数：

[
U(X) = \frac{1}{2} C(X)^T \alpha^{-1} C(X)
]

其中：

α⁻¹：块对角柔度矩阵（Block diagonal compliance matrix）
**C(X)**：约束函数

XPBD的优势：

XPBD有一个很大的好处，就是它可以给逐条的约束增加它的stiffness。简单来讲，就比如说像这里面展示的一个案例，就是那个硬币在来回的抖动，他这个约束呢就是一个非常硬的约束，这个时候它的stiffness就会设的很高，你能看到那种非常合理的这种高频的抖动。

大家知道其实在传统的物理模拟里面，刚体模拟里面这个case是比较难解决的。但是呢对于比如说软的布料、软的布料，或者是一些我们叫做柔性的或者可塑性的形体的话，这个stiffness我就可以放得比较弱。

而这些东西放到一起之后，特别是布料，我是比较柔软的，所以有些约束我其实可以约束的轻一点。那我就可以在一个方程里面，根据对每条约束设定它的stiffness的话，我就可以一个方程把它解出来。这其实是我个人认为XPBD最大的好处。

个人理解：

如果你把这个约束想象成一个弹簧，那么这个stiffness你可以把它理解成就是弹簧的硬度。就是它为零的时候，这个弹簧硬度就无穷大。那么它的倒数就是虎克常数。那么C(X)是什么呢？就是那个偏移量，或者叫做误差，你可以理解成位移。那么一个弹簧它的误差偏移量多少的时候，是不是就是二分之一KX平方？大家可以推导一下，一个弹簧所储存的势能，就是你把它从Rest pose拉开来的位移的平方。

但是如果这个不是一个单一维的弹簧，它可能是个多维的系统的时候，实际上你把这个约束，就会变成一个矩阵的形式。那矩阵乘以矩阵的转置，中间再加上一个这样的一个stiffness的话，实际上从它的这个数学的逻辑上，其实你可以认为，就是说这个系统内涵的一种势能，它本质上就是让你去优化，让这个势能足够的小。

现代应用：

XPBD在现代的游戏引擎里面的话，已经越来越popular，这也是我们现在也比较关注的一个方向。但是呢很遗憾的就是说，这个东西是刚刚这两年兴起的，还没有经过工业化的大规模检验。其实我们也在看，比如说这个算法的稳定度，这个算法的数值的可控性和精度，是不是能保证住，包括在对于游戏各种各样复杂的场景。

因为游戏对这个物理式的表达，它不仅是物理的模拟的真实性，还有很多的可控性。那么这一点的话呢，实际上也是现代物理引擎一个比较前沿的一个发展方向。

总结

PBD和XPBD是建立在拉格朗日力学基础上的高级物理仿真技术：

拉格朗日力学：把物理规律描述成约束，用约束反向定义运动
雅可比矩阵：表示约束的变化趋势，指导迭代方向
PBD核心思想：把物理系统描述为位置约束，通过迭代投影满足约束
PBD工作流程：初始化 → 预测位置 → 生成碰撞约束 → 迭代投影约束 → 更新状态
XPBD扩展：引入刚度概念，可以为不同约束设置不同的stiffness，实现硬约束和软约束的统一处理

PBD是一个非常经典的思想，它最早的文章应该是2007年的文章，那篇文章还发表了一个非常小的会议上，但是确实是一个非常巧妙的思想。现在在布料模拟、医疗模拟等领域，PBD已经成为了主流方法。而XPBD作为PBD的扩展，正在成为现代物理引擎的前沿方向。

转载请注明来源，欢迎对文章中的引用来源进行考证，欢迎指出任何有错误或不够清晰的表达。可以在下面评论区评论，也可以邮件至 785293209@qq.com